对流层延迟改正方案对GPS/BDS动态PPP定位精度的影响
艾力·库尔班,何秀凤,章浙涛
对流层延迟改正方案对GPS/BDS动态PPP定位精度的影响
艾力·库尔班,何秀凤,章浙涛
(河海大学 地球科学与工程学院,南京 211100)
针对全球卫星导航系统(GNSS)高精度导航定位易受到对流层延迟误差影响的问题,提出采用全球定位系统(GPS)和北斗卫星导航系统(BDS)组合定位的方法进行动态精密单点定位(PPP):以GPS定位结果为参照,对GPS/BDS组合定位结果进行评估;然后对比分析传统方法(无改正方案)、Saastamoinen模型和天顶对流层延迟(ZTD)参数估计法得到的GPS/BDS组合PPP结果差异。实验结果表明:GPS/BDS组合定位相对于GPS有利于提升定位解算精度,并且可以有效地缩短收敛时间;3种对流层延迟改正方案对PPP定位精度的影响有所不同,水平方向定位精度差异较小,高程方向定位精度有着显著差异;Saastamoinen模型和ZTD参数估计法收敛时间基本保持一致,平均收敛时间大约为60 min,而传统方法平均收敛时间为90 min;此外,采用Saastamoinen模型得到的定位精度表现最佳,可以为GPS/BDS组合动态PPP定位提供1.20 cm以内的水平精度和3.00 cm以内的高程精度。
精密单点定位;对流层延迟;Saastamoinen模型;天顶对流层延迟参数估计法;收敛时间;定位精度
0 引言
精密单点定位技术(precision point positioning, PPP)是指采用单台单频或单台多频全球卫星导航系统(global navigation satellite system, GNSS)接收机,利用码伪距和载波相位观测值以及由国际GNSS服务组织(International GNSS Service,)分析中心提供的精密卫星钟差产品和精密星历来实现毫米级精度定位的方法。PPP技术与其他定位技术比较具有无需基准站、不受距离的影响、操作灵活简单、精度高和成本低等优势,因此受到广大GNSS用户的青睐。目前PPP技术已经在卫星定轨测量、自然灾害监测、地球地表形变监测、桥梁高精度形变监测等导航定位领域得到广泛的应用[1-6]。但是PPP技术容易受到信号传播路径中大气层延迟误差的影响,其中对流层延迟误差的影响是不可忽略的。为了提高PPP定位性能和精度,必须对对流层延迟误差进行改正处理[7]。
GNSS信号在传播过程中对流层效应与频率无关,因此不能采用多频观测值组合的方法来消除或减弱对流层延迟误差对定位精度的影响,只能采用模型或其他方法。对流层延迟误差一般采用经验模型法、参数估计法、外部修正法等方法进行改正[8]。常用的经验模型包括Saastamoinen模型[9]、Black模型[10]、改进的Hopfield模型[11]、欧洲静地导航覆盖服务(Europe geostationary navigation overlay service, EGNOS)模型[12]和加拿大新不伦瑞克大学(University of New Brunswich,UNB3)模型[13]等。Saastamoinen模型、Black模型和改进的Hopfield模型都需要大量的测站实测气象数据,而EGNOS和UNB3模型都是依靠大量的观测资料形成的。文献[14-18]中采用这几种模型都可以在不同程度上减小对流层延迟误差以提高定位精度,其中PPP定位精度可以达到厘米级。
Saastamoinen模型虽然有一定的局限性,但该模型相对于其他经验模型而言少了1个温度误差改正项,而且充分考虑到了对流层垂直高度的影响;同时不需要大量的观测资料,可以在精度方面对对流层延迟误差进行改进,所以在PPP定位中应用较为广泛。目前Gamit和Bernese等高精度数据处理软件均采用Saastamoinen模型来改正对流层延迟误差。在实际生产应用中,大气中的水汽是时刻随着时空变化呈现随机变化的,很难直接精确地测定气象数据,这将会直接导致载波相位整周模糊度固定解算失败或者测站坐标高程方向解算精度较差。遇到类似问题的时候可以选择天顶对流层延迟(zenith tropospheric delay, ZTD)参数估计法来改正对流层延迟误差。参数估计法是将天顶方向的对流层延迟作为待估参数进行解算,通过平差来估计其精确值。根据观测时段的长度和观测时的气候状况等因素可以对待估参数作不同处理。第1种方法是单参数法,每个测站整个时段中只引入1个天顶方向对流层延迟参数进行计算;第2种方法是多参数法,将整个时段分为若干个子区间,每个区间各引入1个参数进行计算。
随着世界各国卫星导航系统不断的建设完善和应用推广,多系统兼容、互操作与组合定位已经成为GNSS导航定位领域内主要发展趋势之一。目前国内有大量研究者不断深入研究全球定位系统(global positioning system, GPS)对流层延迟误差改正方案,但是鲜有对GPS及北斗卫星导航系统(BeiDou navigation satellite system, BDS)组合PPP的对流层延迟改正作研究。因此,本文首先比较GPS/BDS组合定位和GPS定位解算精度,然后对GPS/BDS组合定位收敛时间和定位精度进行评估,最后重点对传统方法(无改正方案)、Saastamoinen模型和ZTD参数估计法进行比较,并通过实测数据对比分析3种不同改正方案对GPS/BDS组合动态PPP定位精度的影响。
1 对流层延迟改正模型
卫星信号经过大气层的对流层部分时会产生非色散性延迟,使得信号传播的实际路径比理论上的几何距离变长,这就造成了对流层延迟误差。一般基于模型修正法的对流层延迟模型通常是将信号传播路径上的对流层延迟分为测站天顶方向的对流层延迟和映射函数(mapping function, MF)2部分的乘积[19]。而天顶方向对流层延迟又可以模型化为2部分,即天顶静力学延迟(zenith hydrostatic delay, ZHD)和天顶湿延迟(zenith wet delay, ZWD)。映射函数也分为干、湿映射函数。典型映射函数模型的Marini连续映射函数模型、Vienna投影函数(Vienna mapping function 1, VMF1)模型、Nell投影函数(Nell mapping function, NMF)模型和全球投影函数(global mapping function, GMF)模型等。不同的映射函数所用的参数不同,因此映射函数的好坏也将直接影响对流层延迟改正效果。
1.1 基本观测方程
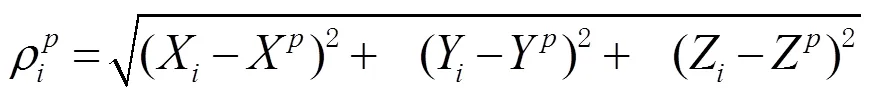
码伪距基本观测方程可以写为

载波相位基本观测方程可以写为
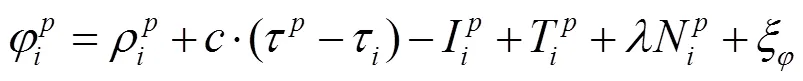
1.2 Saastamoinen模型
Saastamoinen模型于1973年由Saastamoinen根据气体定律提出,在PPP中有较为广泛的应用。它是1个由测站维度、高程、观测高度角、干温和水汽为自变量的函数,在实际应用中需要测量当地的有关气象参数。
模型理论计算公式为

其中
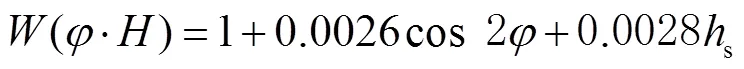
经数值拟合后上述公式可表示为
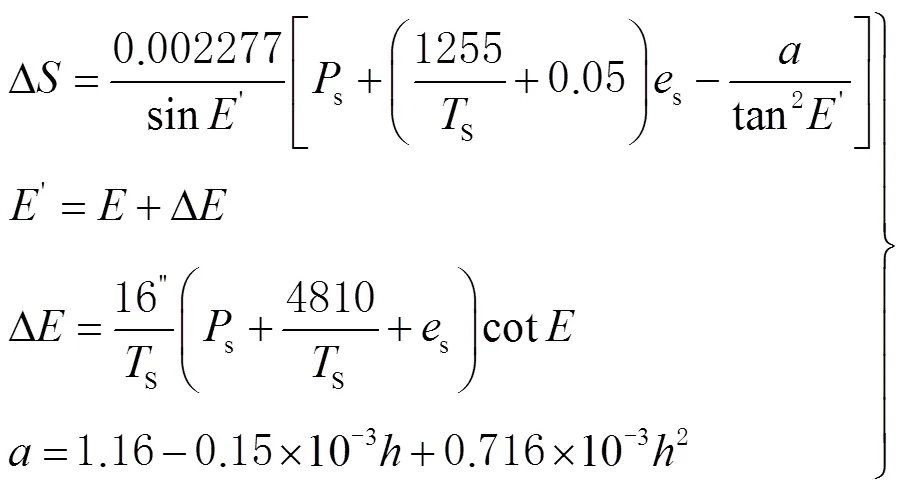
1.3 ZTD参数估计法
在高精度测量时,采用ZTD参数估计法估计天顶方向对流层总延迟。在数据处理过程中将它作为未知参数与接收机钟差、接收机坐标参数、整周模糊度等未知量一起进行解算,从而达到精确估计对流层延迟误差、提高定位的精度的目的。同时,本文实验中观测时段长度较短,测站之间距离较短,测站周围气候稳定,所以采用单参数估计法。
对流层总延迟计算公式为


2 实验与结果分析
实验选取南水北调工程双王城水库4个测站2017年年积日第250天24 h的GNSS观测数据,利用武汉大学IGS数据中心提供的30 s精密星历和30 s精密卫星钟差产品进行PPP定位解算。同时为了减少其他模型误差对实验结果的影响,实验中采用GPS/BDS组合定位,卫星高度角设为10°,接收机的采样间隔为15 s。不同处理方案电离层延迟改正都采用消电离层组合双频改正模型,且都利用IGS提供的卫星和接收机天线平均相位中心变化(phase center variation, PCV)校正文件、卫星码间偏差(differential code bias, DCB)产品、地球自转参数(Earth rotation parameter, ERP)改正文件和海洋潮汐负荷(ocean tide loading,OTL)校正文件对其他误差进行改正。双王城水库所选的测站分布情况如图1所示。表1为测站相关信息。

图1 双王城水库GNSS测站分布
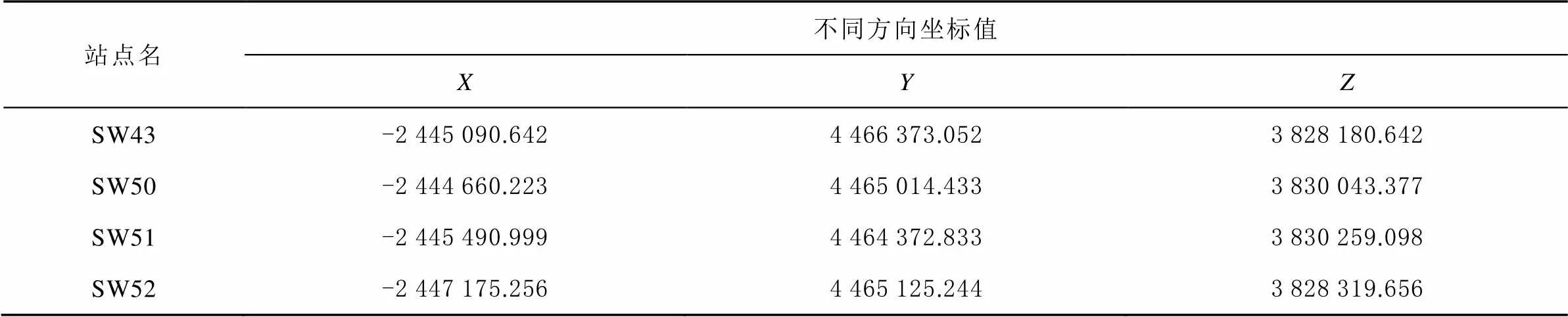
表1 测站WGS84坐标信息 m
2.1 GPS/BDS和GPS对比分析
为了验证GPS/BDS组合定位效果,以SW51测站为例,将GPS/BDS组合定位结果与单独GPS定位结果作对比,结果如图2~图4所示。图2为GPS/BDS组合定位和GPS定位收敛时间比较。本文中收敛时间定义为从开始解算的历元起,北()、东()和天()方向的定位误差均优于15 cm。为确保结果的可靠性,同时检查首次收敛时刻后续20个历元的定位误差,只有当20个历元定位误差都在±15 cm以内时,才认为从开始解算的历元到该历元所需的观测时间为PPP收敛时间[20]。根据图2可以看出,GPS/BDS组合定位收敛时间用时更短,尤其是在和2个方向的组成的水平方向收敛时间明显少于GPS。经过计算可知,GPS/BDS组合定位平均收敛时间为60 min,而GPS平均收敛时间为90 min,GPS/BDS组合定位有助于缩短收敛时间。图3为GPS/BDS组合定位和GPS定位误差比较,组合定位误差明显小于GPS,方向最为明显,方向相当。由计算可知,SW51测站GPS/BDS组合定位、和方向的定位误差均方根(root mean square, RMS)分别为0.93、0.47和1.55 cm,GPS定位、和方向的RMS分别为1.80、0.62和2.41 cm。图4为GPS/BDS组合定位和GPS定位精度比较。通过比较可知,GPS/BDS组合定位结果要明显优于GPS,其定位结果较GPS在方向上分别提高了86 %、13 %和35 %。
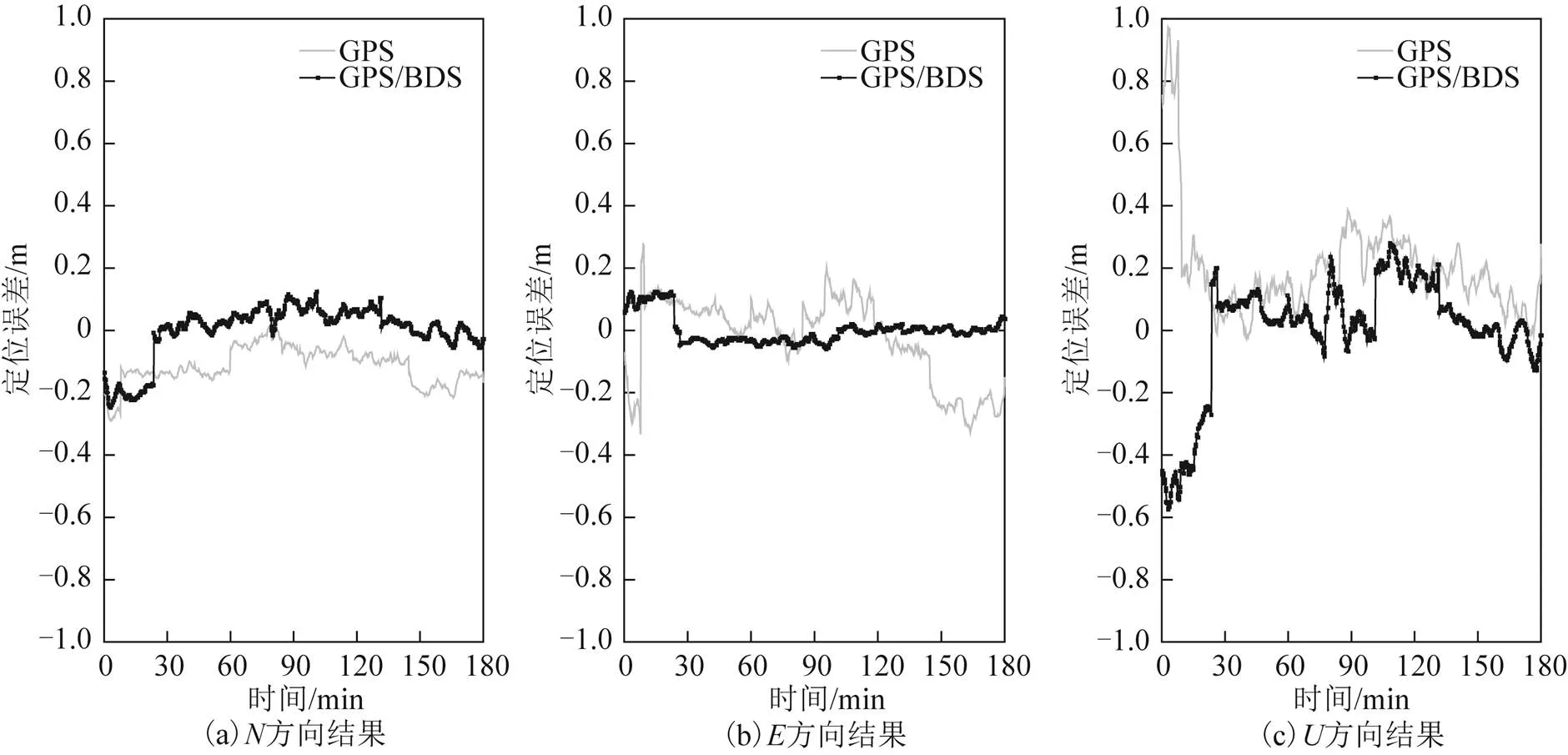
图2 SW51测站GPS/BDS与GPS收敛时间比较
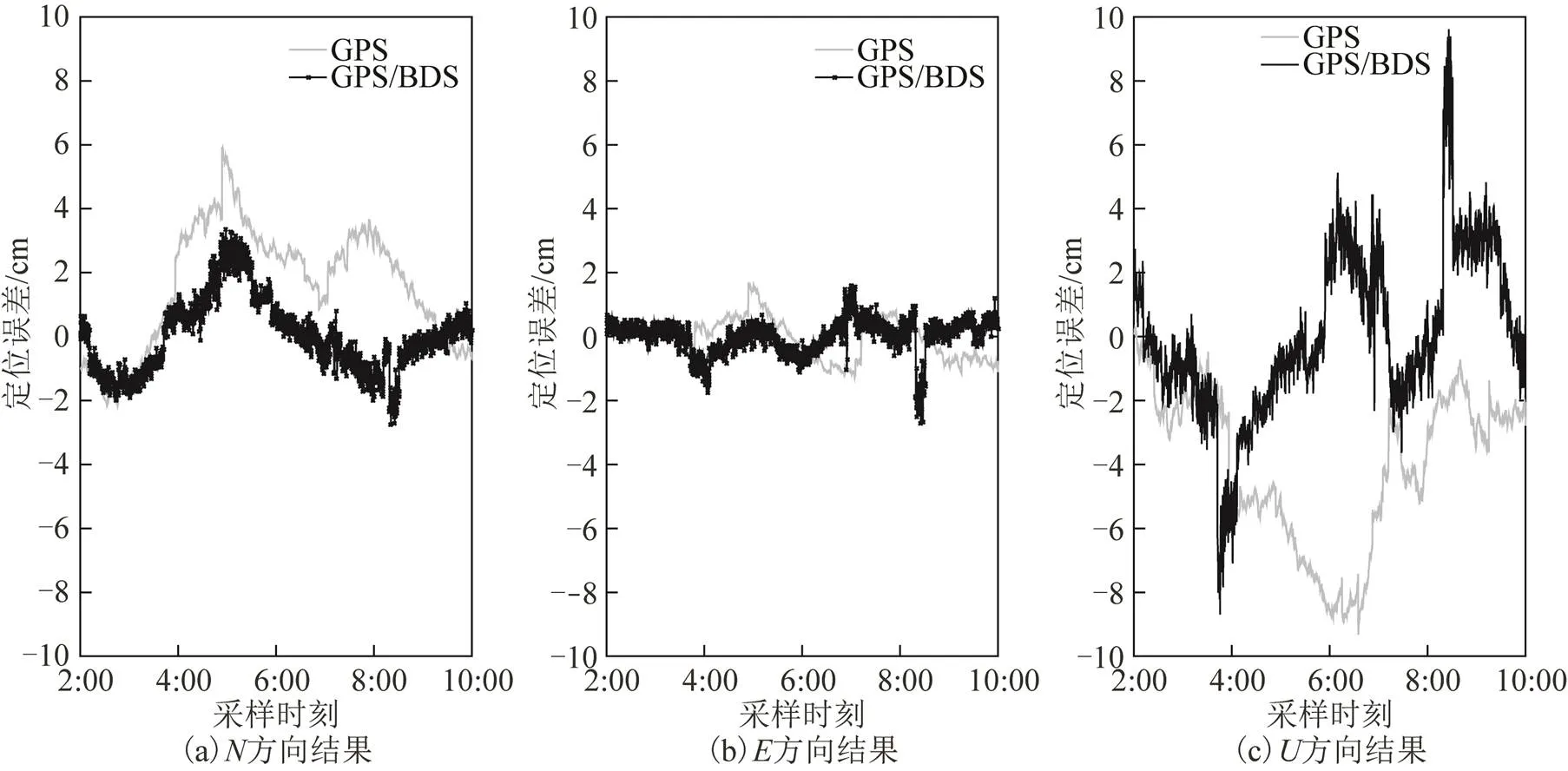
图3 SW51测站GPS/BDS与GPS定位误差比较
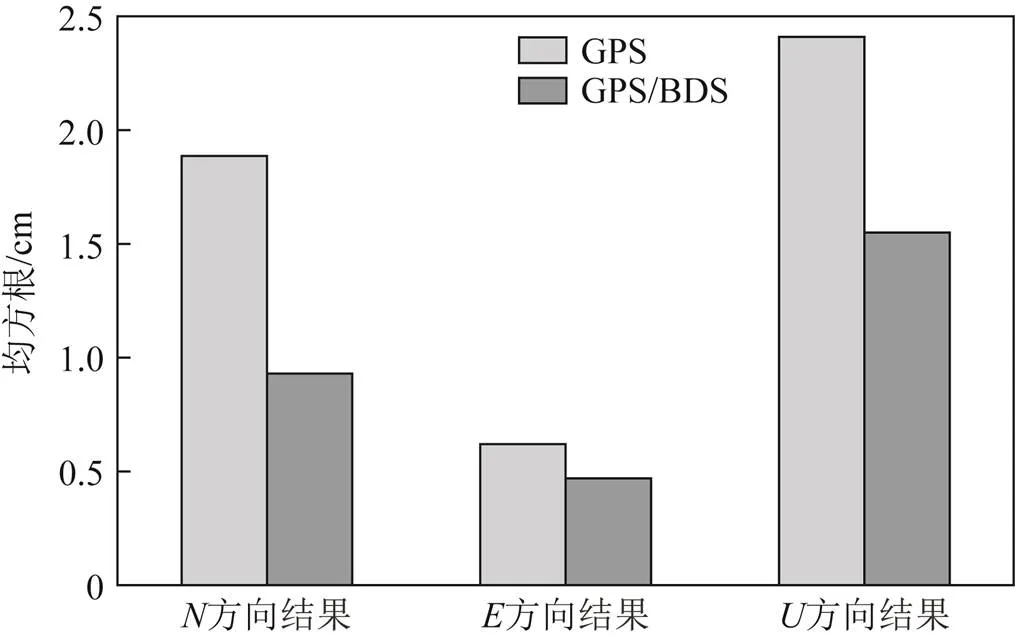
图4 SW51测站GPS/BDS与GPS定位精度比较
2.2 不同方案收敛时间分析
在动态模式下分别用传统方法、Saastamoinen模型和ZTD参数估计法进行GPS/BDS组合PPP定位解算。对比分析采用3种改正方案得到的定位误差时间序列。为了分析初始收敛时间,选取实验数据解算结果的开始3 h部分(GPS时00:00:00—03:00:00)进行分析。以SW51测站解算结果为例,结果如图5所示。图5中,NONE代表传统方法,SAAS代表Saastamoinen模型,ZTD代表ZTD参数估计法。
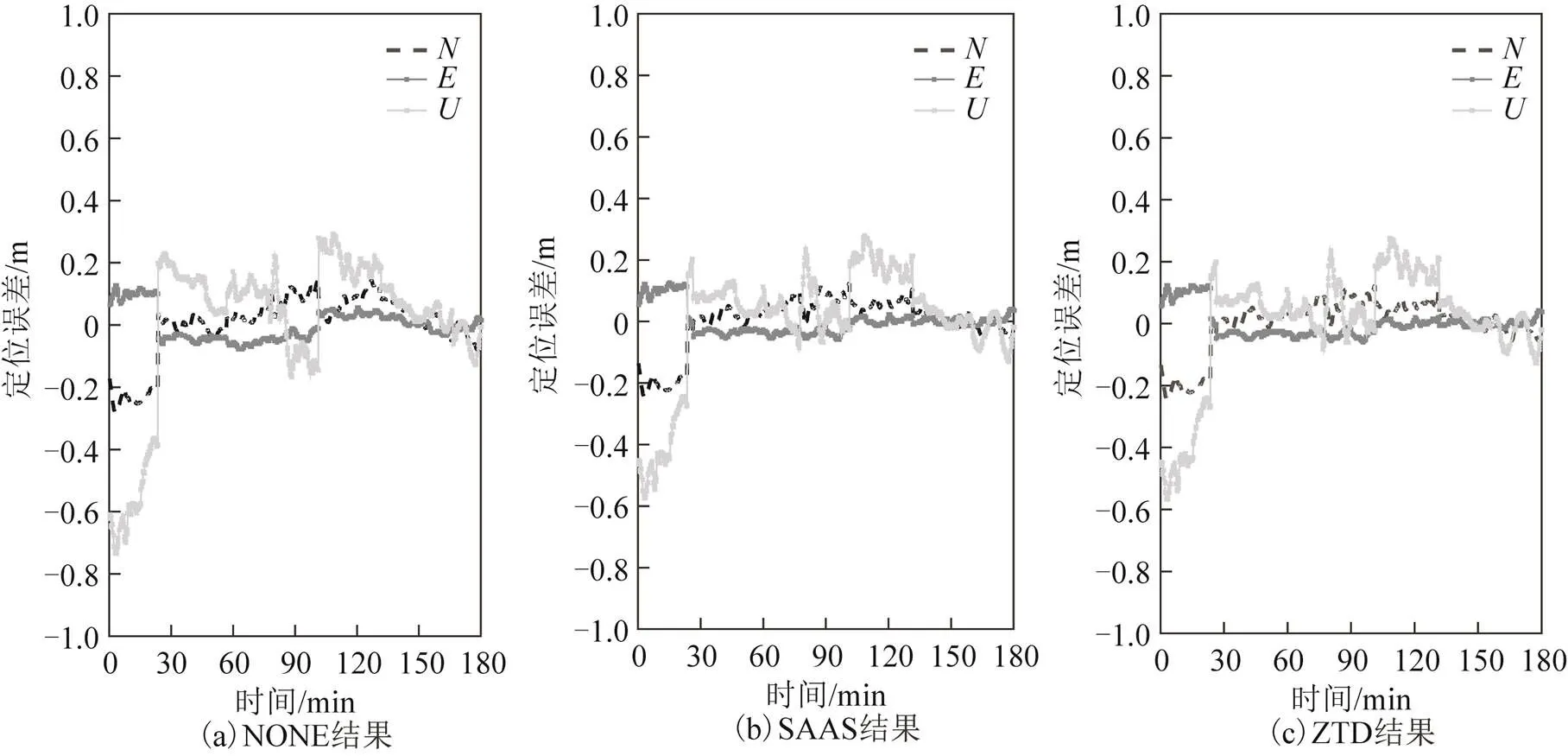
图5 SW51测站不同方案收敛时间比较
从图5中可以看出,传统方法水平方向至少需要60 min收敛,高程方向至少需要120 min。而SAAS模型和ZTD参数估计法收敛时间大致保持一致,水平方向大约需要30 min收敛,高程方向需要90 min收敛。通过计算平均收敛时间得知,SAAS模型和ZTD参数估计法的平均收敛时间相当,60 min就可以收敛;传统方法平均收敛时间最长,至少需要90 min才收敛。
2.3 不同方案定位精度分析
为了分析初始收敛之后的定位效果,选取收敛之后的8 h部分(GPS时02:00:00—10:00:00)进行分析。结果如图6所示。图6为SW51测站不同方案定位误差时间序列。可以看出,3种方案水平方向定位误差明显优于高程方向定位误差,且大部分时间内优于±2 cm。在高程方向,传统方法定位误差大部分时间在±6 cm以内,SAAS模型定位误差在±4 cm以内,ZTD参数估计法在±8 cm以内。这是因为目前可观测的GNSS卫星数目较多,几何分布也较为均匀,所以天顶方向对流层延迟误差主要影响测站的高程,对平面位置的影响较小。同时可以看出采用3种方案得到的和方向定位误差有差异,方向差异较为明显,并且方向定位误差相对于方向和方向更为稳定且最小。从整体上看,SAAS模型定位误差最小且水平方向和ZTD参数估计法相近。ZTD参数估计法高程方向定位误差最大。
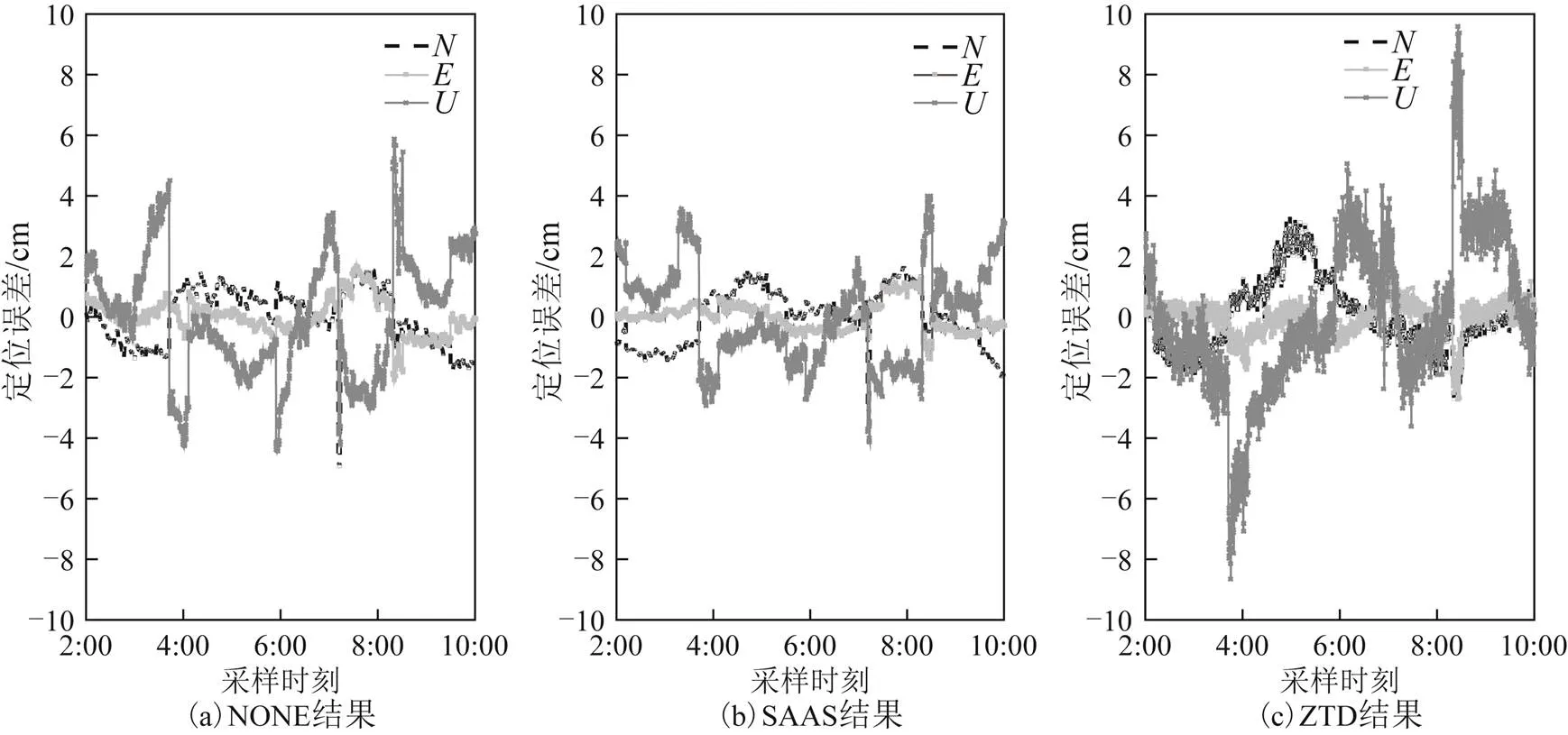
图6 SW51测站不同方案定位误差时间序列
为了进一步比较3种对流层延迟处理方案的收敛后的PPP定位精度及可靠性,对解算结果进行统计,计算其定位误差RMS。表2分别给出了4个测站不同的对流层处理方案得到的定位误差RMS。

表2 不同方案定位误差均方根 cm
从表2中可以得出,4个测站采用不同处理方案可以得到厘米级的定位精度。水平方向定位精度都优于1.20 cm,SAAS模型定位精度优于其他2个方案,可以达到亚厘米级;同时SAAS模型和ZTD参数估计法定位精度相当。在高程方向,传统方法定位精度优于3.00 cm,SAAS模型优于1.55 cm,ZTD参数估计法优于2.60 cm。整体而言,SAAS模型定位精度最佳。值得注意的是:SAAS模型是经验模型,主要对天顶方向对流层干延迟做改正;因为天顶方向干延迟占总延迟的比重较大,占总延迟的90%左右,所以模型改正效果相对较好。而采用ZTD参数估计法使定位方程待估参数增多,降低了数据解算的稳定性,参数估值容易受对流层延迟误差和病态方程的影响,导致改正效果相对较差。同时,我国周围环境复杂,沿海地区的水汽分布在空间上分布不均匀,时间上变化又较快等因素,很难准确测定对流层湿延迟分量。这也是ZTD参数估计法改正效果较差的重要原因。
为了定量分析收敛后的PPP定位精度,图7给出了不同测站采用不同处理方案在和3个方向定位误差RMS比较。从图7中可以看出,SW50测站定位精度最好,SW52测站最差。方向上,SAAS模型定位精度相对较好,ZTD参数估计法较差;方向上,SAAS模型和ZTD参数估计法定位精度基本保持一致且优于传统方法;方向上,SAAS模型定位精度相对较好,传统方法较差。整体而言,SAAS模型定位精度表现得更为稳定。

图7 不同方案定位误差RMS比较
3 结束语
本文主要通过比较采用3种不同对流层延迟处理方案得到的GPS/BDS动态PPP解算结果,从收敛时间、定位误差和RMS等方面进行对比,得出以下结论:
1)GPS/BDS组合定位相对于GPS定位有利于提升定位解算精度并且可以有效地缩短初始的收敛过程。
2)Saastamoinen模型与ZTD参数估计法的收敛时间基本保持一致,平均收敛时间大约为60 min。而传统方法平均收敛时间为90 min。整体而言,Saastamoinen模型收敛时间相对较短,传统方法收敛时间最长。
3)整体来看,不同的对流层延迟改正方案对GPS/BDS组合PPP定位精度影响不同,对水平方向定位精度影响较小,对高程方向定位精度影响最为明显。3种方案定位精度均能达到厘米级。采用Saastamoinen模型得到的定位精度表现最佳且最为稳定,可以为GPS/BDS组合动态PPP定位提供1.20 cm以内的水平精度和3.00 cm以内的高程精度。
[1]ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al.Precise point positioning for the efficient and robust analysis of GPS date from large networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5005-5017.
[2]OUBA J, HEROUX P. Precise point positioning using IGS orbit and clock products[J]. GPS Solutions, 2001, 5(2): 12-28.
[3]魏二虎, 刘学习, 王凌轩, 等. BDS/GPS组合精密单点定位精度分析与评价[J]. 武汉大学学报(信息科学版), 2018, 43(11): 1654-1660.
[4]张锡越, 赵春梅, 王权, 等. 多系统融合单频精密单点定位[J]. 测绘科学, 2018, 43(3): 29-34.
[5]张小红, 刘经南, RENE Forsberg. 基于精密单点定位技术的航空测量应用实践[J]. 武汉大学学报(信息科学版), 2006, 31(1): 19-22.
[6]袁修孝, 付建红, 楼益栋. 基于精密单点定位技术的GPS辅助空中三角测量[J]. 测绘学报, 2007, 36(3): 251-255.
[7]刘晨, 郑南山, 丰秋林. 全球对流层延迟模型的质量评价[J]. 大地测量与地球动力学, 2018, 38(10): 1005-1010.
[8]李征航, 黄劲松. GPS测量与数据处理(第二版)[M]. 武汉: 武汉大学出版社, 2013.
[9]SAASTAMOINEN J. Contributions to the theory of atmospheric refraction[J]. Bulletin Geodesique, 1972, 106(1): 383-397.
[10]BLACK H D. An easily implemented algorithm for the tropospheric range correction[J]. Journal of Geophysical Research: Solid Earth, 1978, 83(B4): 1825-1828.
[11]HOPFIELD H S. Tropospheric effect on electromagnetically measured range: prediction from surface weather data[J]. Radio Science, 1971, 6(3): 357-367.
[12]黄良珂, 刘立龙, 周淼, 等. 亚洲地区EGNOS天顶对流层延迟模型的精度评估[J]. 大地测量与地球动力学, 2013, 33(4): 128-132.
[13]周命端, 郭际明, 孟祥广. GPS对流层延迟改正UNB3模型及其精度分析[J]. 测绘信息与工程, 2008, 33(4): 3-5.
[14]李昭, 邱卫宁, 邱蕾, 等. 几种对流层延迟改正模型的分析与比较[J]. 测绘通报, 2009(7): 16-18.
[15]施展, 孟祥广, 郭际明, 等. GPS精密单点定位中对流层延迟模型改正法与参数估计法的比较[J]. 测绘通报, 2009(6): 9-11.
[16]陈瑞琼, 刘娅, 李孝辉. 卫星导航系统中对流层改正模型分析[J]. 测绘通报, 2015(3): 12-15.
[17]王君刚, 陈俊平, 王解先, 等. 对流层经验改正模型在中国区域的精度评估[J]. 武汉大学学报(信息科学版), 2016, 41(12): 1656-1663.
[18]赵祥伟, 陈正宇. 全球天顶对流层延迟模型新修正方法[J]. 测绘科学, 2018, 43(5): 18-22, 61.
[19]姚宜斌, 张豹, 严凤, 等. 两种精化的对流层延迟改正模型[J]. 地球物理学报, 2015, 58(5): 1492-1501.
[20]张小红, 左翔, 李盼, 等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250-256.
Influence of tropospheric delay correction schemes on GPS/BDS kinematic PPP positioning accuracy
(School of Earth Sciences and Engineering, Hohai University, Nanjing 211100, China)
Aiming at the problem that it is susceptible to tropospheric delay errors for precise navigation and positioning of GNSS, the paper proposed to use the combination of GPS with BDS in the kinematic precise point positioning (PPP): the positioning results of GPS/BDS were compared with those of GPS, and the differences of GPS/BDS PPP output between the traditional method (without the correction scheme), Saastamoinen model and ZTD parameter estimation were comparatively analyzed. Experimental result showed that GPS/BDS combined method could be more beneficial to improve the positioning solution accuracy, and more efficiently shorten the convergence time than GPS; moreover, the three tropospheric delay correction schemes would have different effects on PPP positioning accuracy, in which the horizontal positioning results would be similar, while the vertical positioning results would have significant differences; meanwhile, the convergence time of Saastamoinen model and ZTD parameter estimation method would be basically the same,with an average convergence time about 60 min, however, that of the traditional method would be almost 90 min; in addition, GPS/BDS combined kinematic PPP positioning accuracy obtained by the Saastamoinen model woud be the best, which could provide the horizontal and vertical accuracy within 1.20 and
precise point positioning; tropospheric delay; Saastamoinen model; zenith tropospheric delay (ZTD) parameter estimation; convergence time; positioning accuracy
P228.4
A
2095-4999(2020)02-0069-07
3.00 cm, respectively.
艾力·库尔班,何秀凤,章浙涛. 对流层延迟改正方案对GPS/BDS动态PPP定位精度的影响[J]. 导航定位学报, 2020, 8(2): 69-75.(KUERBAN Aili, HE Xiufeng, ZHANG Zhetao. Influence of tropospheric delay correction schemes on GPS/BDS kinematic PPP positioning accuracy[J]. Journal of Navigation and Positioning, 2020, 8(2): 69-75.)
10.16547/j.cnki.10-1096.20200212.
2019-08-23
国家自然科学基金重点项目(41830110)。
艾力·库尔班(1990—),男(维吾尔族),新疆温宿人,硕士研究生,研究方向为卫星导航与定位。
何秀凤(1962—),女,江苏泰州人,博士,教授,研究方向为卫星导航定位、变形监测技术、InSAR和GPS集成技术。
——环地平弧&环天顶弧

