线上线下混合式教学模式中融入课程思政的探讨

【摘 要】通过线上线下混合式教学模式的初步应用探索，教学成果显著有效。在线性代数课程教学中融合思政教育，将知识传授与思想教育恰当结合，不仅能提高学生的学科知识素养，更有利于学生的思想建设。高校教师应肩负起时代使命，培养德才兼备的“本科水平，一专多能”的应用型人才。

【关键词】混合式教学;线性代数;课程思政

【中图分类号】G642  【文献标识码】A  【文章编号】1671-8437（2020）28-0003-03

2016年全国高校思想政治会议召开后，在各科课程中融入思想政治教育越来越受到高校教师的重视[1]。而利用线上线下混合教学模式，结合线性代数课程的知识结构，在线性代数课程教学中融入思政教育正是高校教师积极探索的。

1   线上线下混合式教学模式的初步探索

1.1  线上线下混合式教学的定义

线上线下混合式教学是一种集传统班级授课的优势与数字化教学中个性化学习于一体的杂糅式教学方式，具有动态鲜明、开发及时的特点。简而言之，就是将传统教学的优势和数字化教学的优势结合起来，在保留传统教学模式优势的同时，尝试使用信息技术，形成一种融合式的教学形态。这样做能够实现传统教学与信息化教学的优势互补，从而获得更佳的教学效果。

1.2  线上线下混合式教学的利与弊

线上线下混合式教学是本科阶段的重要教学模式，也是提高教学质量的重要手段，特别是在线性代数这门课程中，应用线上线下混合式教学模式，将复杂的运算步骤通过数字化教学来展示，能使学生更容易理解所学内容，更牢固地掌握知识点。学生课后可通过在线回放教学视频来巩固自己薄弱的知识点;想深入探究学习的学生，可在线回放教学视频，将重点知识梳理;准备考研的学生，可通过线上视频回放学习，为数学科目的考试提前做准备。但线上线下混合教学模式也有弊端，如线上教学时，学生课上的学习状态难以得到教师的监测、学生的学习积极性无法掌握等。

1.3  如何开展线上线下混合式教学

在2019—2020第二学期，无锡太湖学院线性代数教研室采用了线上线下混合教学模式，在16周的授课中，1—4周学生进行慕课学习，提前学习国内双一流大学的线性代数慕课课程，目的是初步了解线性代数这门课程，理解课程纲要，了解所学内容，为进一步深入学习做好准备;5—14周进行教师线上授课，任课教师通过视频直播课程，带领学生深入学习线性代数这门课程的具体知识。在授课过程中融合思政教育，通过课堂互动、提问、讨论、小组合作探究、小组合作完成案例作业，让学生在理解所学内容的基础上，充实头脑，完善思维;15—16周进行线下教学，教师在教室针对疑难问题，对学生进行个性化教学，通过严谨细致的解题方法及解题技巧的讲解，让学生知道，只要肯钻研、肯努力，再难的问题都会得到解决，最终都将到达成功的彼岸。通过2019—2020第二学期的教学实验，线性代数这门课程的教学效果明显提升，学生期末考试通过率达89%。

2   思政教育与线性代数课程体系

2.1  肩负时代使命，培养德育人才

新时代高等教育的根本任务是立德树人。在人才培养的过程中，培养什么人、怎样培养人、为谁培养人是必须回答好的根本问题。高校教师要利用好课堂教学这个主渠道，使各类课程与思想政治理论课同向同行，形成协同效应[2]。由此，课程思政作为一种重要的教育理念，逐步在高等教育界得到认可，进而在高校所有课程的教学中肩负起价值引领的责任[3]。

2.2  立足课程体系，融入思政教育

对线性代数的课程内容、线上线下混合式教学的特点进行全面而深入的研究后，笔者认为，融入课程思政教育的线性代数课程体系应该满足四个基本要求：一是符合线性代数课程的教学目标，即课程知识的学习目标;二是符合课程思政教育的需要，即实现课程思政教育的目标;三是符合思政教育系统化的原则，思政教学内容应系统地贯穿课程始终;四是符合思政内容与线性代数课程内容和谐化的原则，即思政内容自然和谐地融入课程之中，既不突兀、又不牵强[4]。

该校教师基于线性代数课程体系构建的四个基本原则，通过比较国内外线性代数课程教学体系，结合课程思政教育内容，确定了“三基、一核心、二应用”的线性代数课程体系，即“以行列式、矩阵及向量组为基本工具，以线性方程组的求解方法为核心，系统地解决矩阵的相似对角化与二次型的标准化问题[5]”。在具体的教学中，将课程内容分为三大部分，第一部分是学习行列式、矩阵、线性方程组;第二部分是学习线性方程组的求解及解的结构;第三部分是学习矩阵的相似正交化及对角化。三部分的课程内容划分是依照教学目标，融合思政教育，体现数学思想，将线性代数教学与课程思政教育协调一致进行的，知识由简到繁，由基础到复杂，可以让学生在无形中理解无论是学习还是做事情，都是要在拥有一定基础和能力的前提下，才能更好地进入下一阶段，取得更好的成绩，收获成功，实现自己的理想。

3   在线性代数教学中融合课程思政

3.1  细节之处见成败

在讲解行列式与矩阵的区别时，教师可以融合思政教育，引导学生注意细节，养成严谨的求学态度。在讲解矩阵与行列式的基本概念时，教师都会先提醒学生行列式与矩阵的本质区别：行列式是一个数值，而矩阵是一个有序数表;在表达形式上，行列式用两条线段将元素包括在内，而矩阵用中（小）括号将元素包括在内。强调本质与形式上的区别后，引导學生理解做事情最基本的方法是要具有严谨细致认真的求学态度，否则就无法提高，无法进入下一阶段。无论是在生活中还是学习中，只有一点一滴地积累，才能积少成多、汇流成河，才能让人生闪闪发光[6]。

3.2  揭开表象看本质

在讲解求矩阵秩的方法时，教师可以融合思政教育，引导学生透过表象看本质，只有看清事物的本质，才能不迷失方向，在正确的道路上坚定地走下去。

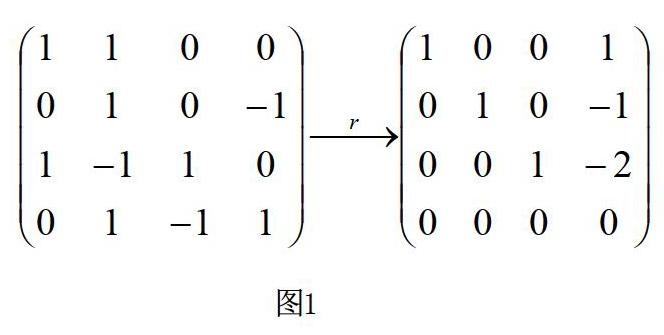
在讲解求如图1矩阵秩时，教师阐述求解逆矩阵的方法就是不断地对矩阵进行初等行变换，直到把原矩阵化简为行阶梯形矩阵。有时题目简单，通过三四步的初等行变换即可把原矩阵化简为行阶梯形矩阵。再观察阶梯形矩阵非零行的个数，有多少个非零行，原矩阵的秩就为多少。但是遇到复杂一点的求矩阵秩的问题时，要进行五六步的初等行变换才能把原矩阵化简为行阶梯形矩阵。无论是简单的题目还是复杂的题目，学生应始终牢记，矩阵的秩本质是要通过阶梯形矩阵来判断，不能由非阶梯形矩阵直接判断。也就是要透过表象看本质，只有透过表象，才能真正看到事物的本质，掌握本质，提高工作效率，缩短工作时间，取得好的结果。

3.3  把握人生方向，树立理想信念

教师在讲解零向量时，也可以融入思政教育，引导学生不要像零向量一样没有方向，要掌握自己的人生方向，拥有坚定的理想信念。零向量0与非零向量在一起，可理解为两个向量垂直，又可以理解为两个向量平行，零向量“仿佛”随时准备着做出改变来顺应其他向量。基于此，教师在讲解过程中，要让学生明白，不能轻易改变自己的原则去顺从他人，要有自己的坚定信念与做事原则，要有正确的价值观和人生观。如果没有理想信念，一个人就会感觉很迷茫，不知道该做什么，不知道做什么才算有意义，所以人生方向与理想信念对每个人都很重要。对于高校教师，帮学生树立理想信念很重要。教师自身的经验是最好的教育素材，可以和学生分享自己的读书经历，如考研时最晚会学习到凌晨两点钟、考研专业课教材至少学习五遍等。教师的这些亲身经历，会引发学生思考：我想成为什么样的人、我要做到比他更努力才有可能成功。教师要鼓励学生敢于树立自己的理想目标，先从小理想开始，如通过CET-4、CET-6、NCRE等。小理想的实现会增强学生的自信心，进而教师再继续鼓励学生，向更大的理想目标努力前进，实现自己的理想。

3.4  激发自己“隐藏”的优点

教师在讲解方程组解的结构时，可以融合思政教育，引导学生“激发”自己的优点，展示自己的多面才能，不能只学习单一技能，要成为“一专多能”的应用型人才。教师在讲解方程组解的结构时，可以引导学生发散思维，思考通过方程组的通解，能学到什么道理或有怎样的启示等。教师应通过提问激发学生思考，组织小组讨论，鼓励学生踊跃交流思想，并结合学生的发言，做出总结。方程组的解就好比一个人，从外在看到的只是解的結构，而深究其内在会发现，其有无数种可能性。每个人都有无限潜能，每个人的人生也都有无限种可能。所以一个人要做的是不断把自身的优点激发出来，去完善自己，为自己创造美好的生活，为社会的发展贡献力量。

3.5  常怀感恩之心

在讲解求向量组极大无关组时，可以融合思政教育，引导学生理解父母的付出和关爱，对此，应常怀感恩之心。在教学求向量组极大无关组时，教师可以把极大无关组中所含的向量类比为父母，把学生类比为除极大无关组外的单个向量。并且告诉学生，用极大无关组可以把向量组中的其余向量表示出来，这就好比父母对我们的爱，在我们背后默默付出，无论我们需要什么，他们都会倾尽所有给予我们，目的是让我们开心快乐，却不求回报。所以，应珍惜父母给予的爱，常怀感恩之心，对父母多一些关心问候，多帮父母做些力所能及的小事情，让父母知道，我们也在爱着他们。

3.6  辩证看待过程与结果

教师在讲解矩阵相似对角化时，可以融合思政教育，引导学生明白做事情要注重过程，把关注的重点放在过程上，结果才可能完美。在求解矩阵相似对角化的过程中，部分学生会感觉到求解过程很繁琐复杂，因此可能忽视求解过程，而把解题重点放在结果上，这样做往往会造成结果是错误的，这也反映出学生没有掌握核心解题方法。部分学生在学习和生活中，往往存在做事情急于求成，急于取得结果，忽视过程重要性的现象，要知道过程决定结果，结果反映过程，没有脚踏实地的付出，结果很可能会很糟。就像考研一样，成功考上自己的理想院校是一个美好的结果，但是每个人在考研过程中的学习态度、努力和付出的程度是不同的。而重视点滴积累、注重学习过程、刻苦努力的学生往往会获得成功，三心二意、急于求成的学生的结果往往都不如意，因为他们虽有理想，但没有付出同等程度的努力。所以，无论做什么事，过程中的每一步都很关键，牢牢把握过程，才能有好的结果。

在本科课程教学中融入思政教育已是高等院校本科教学的重中之重，新时代的高校教师，必须立足时代发展要求，培养德才兼备的人才。要肩负使命，不断丰富思想内涵，提高自身专业素养，将思政教育恰到好处地融入教学中，不仅要提高学生的专业学科知识水平，而且要培养学生的思维品质，培养出“本科水平，一专多能”的应用型人才。

【参考文献】

[1]孙晓青，薛秋芳，秦新强.新工科形式下“课程思政”在《线性代数》课程中的体现[J].当代教育实践与教学研究，2019（13）.

[2]崔岩.精准施策着力提高思想政治理论课教学质量[J].思想理论教育导刊，2017（9）.

[3]梅强.以点引线以线带面：高校两类全覆盖课程思政探索与实践[J].中国大学教学，2018（9）.

[4]黄永清.课程思政理念下《高等数学》课程教学中的几点思考[J].科教导刊（电子版），2019（27）.

[5]曹殿立.线性代数教材建设的认识与实践[J].教育教学论坛，2017（16）.

[6]杨威，陈怀琛，刘三阳，高淑萍，李兵斌.大学数学类课程思政探索与实践——以西安电子科技大学线性代数教学为例[J].大学教育，2020（3）.

【作者简介】

田研（1993～），女，吉林梅河口人，硕士，无锡太湖学院高等数学教师。研究方向：数学教育、应用数学。

Discussion on Integrating Ideological and Political Education into Online-and-Offline Hybrid Teaching

——Taking the teaching of linear algebra as an example

Yan Tian

（Department of Basic Courses， Wuxi Taihu University， Wuxi， Jiangsu， 214064）

Abstract：Through the preliminary exploration of online-and-offline hybrid teaching mode， the teaching results are significant and effective. The integration of the ideological and political education in the teaching of linear algebra has effectively combined with knowledge teaching and ideological education， which can not only improve students' knowledge literacy， but also help students' ideological construction. College teachers should take on the mission of the times and cultivate versatile applied talents with both political integrity and ability.

Key words：hybrid teaching; linear algebra; ideological and political course