基于ESMF算法的永磁同步电机无位置传感器控制

李蕊　何青　陈龙

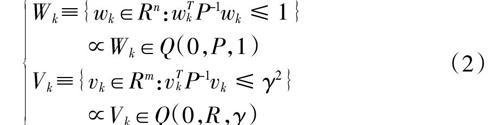
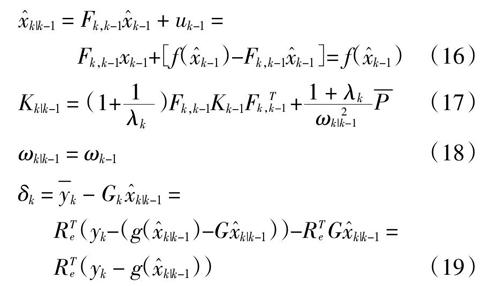
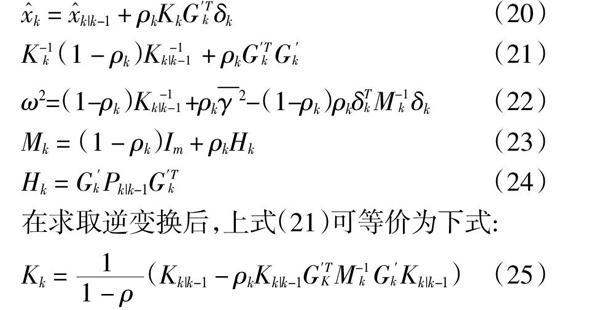
摘   要：论文综合永磁同步电机控制系统和无位置传感器控制技术的分类和发展趋势，主要研究了基于扩展集员滤波的永磁同步电机的无位置传感器的控制系统。结合扩展集员滤波算法（ESMF）建立了基于ESMF的无传感器PMSM矢量控制系统，实时估算电机的转速和位置。对比了测量转速与估计转速，以及测量位置与估计位置，仿真实验结果表明，基于ESMF的无传感器PMSM矢量控制系统具有快速的转速响应特性和良好的稳定性。

关键词：非线性噪声系统;扩展定界椭球;永磁同步电机;无位置传感器控制

中图分类号：TM351                                             文獻标识码：A

Position Sensor-less Control for Permanent Magnet Synchronous

Motor Based on Extension Set Membership Filtering Algorithm

LI Rui？覮，HE Qing，CHEN Long

（Electrical Engineering of Changsha University of science and technology，Changsha，410004，China）

Abstract：This paper integrates the classification and development trend of permanent magnet synchronous motor control system and positionless sensor control technology，and mainly studies the control system of the permanent magnetic synchronous motor based on the expansion collector filter. The Sensor-less PMSM vector control system based on ESMF is established in combination with the expansion set filtering algorithm （ESMF） to estimate the speed and position of the motor in real time. Comparing the measured rotational speed with the estimated rotational speed， as well as the measuring position and the estimated position， the simulation results show that the sensor less PMSM vector control system based on ESMF has fast speed response characteristics and good stability.

Key words：extension set membership filtering algorithm; permanent magnet synchronous motor.

永磁同步电机（PMSM）具有结构简单、重量轻、体积小、速度高、功率小等优点[1-2]。在电机运行时，如果要测量实时永磁转子的磁极位置，传统的方法是在转子轴上安装机械式位置传感器，但是这种办法通常会降低电机的可靠性同时又增加额外成本。为了解决以上问题，研究了基于扩展集员滤波的PMSM无位置传感器控制算法，并通过仿真实验验证了改算法的可行性和优越性。

1   扩展集员滤波算法简介

采用扩展集员滤波（extended set membership filter，ESMF）算法，该算法步骤与EKF方法类似。此方法通过构建椭球预测可行状态集合，求取状态的时间更新，该时间更新求取过程噪声椭球集合以及计算状态转移矩阵椭球集合的并集获得[3]。此外测量更新结果由时间更新得出的状态转移矩阵椭球可行性集合以及测量方程的椭球可行集合求交集得出。

1.1   问题描述

考虑以下加性噪声的非线性系统模型：

xk+1 = f（xk） + wkzk = g（xk） + vk        （1）

其中，f（xk）为二阶可微的状态变量，g（xk）为二阶可微的观测变量;xk∈Rn表示状态向量，zk+1∈Rm表示观测向量;wk∈Rn是过程噪声、vk+1∈Rm是测量噪声。两者满足条件如下：

Wk≡{wk∈Rn：wTkP-1wk ≤ 1}         ∝Wk∈Q（0，P，1）Vk≡{vk∈Rm：vTkP-1vk ≤ γ2}         ∝Vk∈Q（0，R，γ）        （2）

其中γ是实数且满足γ>0，椭球是：

Q（a，k，ω）≡{x∈Rn|（x-a）TK-1（x-a）≤ω2}  （3）

式（3）中K是正定对称包络矩阵、a椭球中心。规定初始状态是：

Q0≡{x0：（x - ■0）Tw-10（x - ■0） ≤ ■0}        （4）

其中■、k0是椭球中心以及对称的正定包络矩阵。

非线性的函数系统由泰勒展开后得到的高阶余项式是：

Rn（xk - ■，Xk） = ■（xr - ■）n+1        （5）

当特殊值nr是1时：

R2（xk - ■，Xk） = ■■（xk - ■）nr+1        （6）

如果是n维状态系统，可知：

R2 = ■diag（XTk，…，wTk）Hes1  ■HesnXk        （7）

式（7）中Hessian矩阵是用Hesn表示的。

■k+1线性化后，状态方程是：

Rg，2（xk - ■k-1，Xk） = ■■（xk - ■k|k-1）2

（8）

■k|k-1线性化后，观测方程是：

Rg，2（xk - ■k-1，Xk） = ■■（xk-■k|k-1）2  （9）

系统线性化后的高阶非线性项不等式是：

||Rf，2（x - ■k-1，Xk）||≤γf||x - ■k-1||2        （10）

||Rg，2（x - ■k|k-1，Xk）||≤γg||x - ■k|k-1||2        （11）

其中||·||是向量的2范数，γf > 0、γg > 0。

线性化后的系统模型是：

xk = Fk，k-1xk-1 + uk-1 + ■k-1■k = Gk xk = ■k        （12）

其中，■k = zk - ？准k，Fk，k-1、Gk是系统雅可比矩阵，另外：

uk-1 = f（■k-1） - Fk，k-1■k-1φk = g（■k|k-1） - Gk ■k|k-1        （13）

■k-1 = Rf，2（x - ■k-1，Xk） + wk-1■k = Rf，2（x - ■k|k-1，Xk） + vk        （14）

式（14）中的虚拟噪声■k、■k被包含于以下的椭球中：

■k≡{■k∈Rn：■Tk■-1■k≤1}∝■k∈Q（0，■，1）■k≡{■k∈Rm：■TkR-1■k≤■2}∝■k∈Q（0，■，■） （15）

1.2   时间更新

■k|k-1 = Fk，k-1■k-1 + uk-1 =

Fk，k-1xk-1+[f（■k-1）-Fk，k-1■k-1]= f（■k-1） （16）

Kk|k-1 = （1+■）Fk，k-1Kk-1FTk，k-1+■■  （17）

ωk|k-1 = ωk-1        （18）

δk = ■k - Gk ■k|k-1 =

RTe（yk-（g（■k|k-1）-G■k|k-1））-RTeG■k|k-1 =

RTe（yk - g（■k|k-1））        （19）

其中δk是系統的预测误差[4]。

1.3   测量更新

假设：R-1 = ReRTe，■k′ = RTe■k和G′k= RTeGk，

则：

■k = ■k|k-1 + ρkKkG′Tkδk        （20）

K-1k（1 - ρk）K-1k|k-1 + ρkG′TkG′k        （21）

ω2=（1-ρk）K-1k|k-1+ρk■2-（1-ρk）ρkδTkM-1kδk  （22）

Mk = （1 - ρk）Im + ρkHk        （23）

Hk = G′kPk|k-1G′Tk        （24）

在求取逆变换后，上式（21）可等价为下式：

Kk = ■（Kk|k-1 - ρkKk|k-1G′TKM-1kG′kKk|k-1）   （25）

2   基于定界椭球的ESMF算法优化

2.1   选择更新策略

为了改善算法的计算效率，采用了一种选择性更新策略[5]：在特定条件下，可以忽略一些无关步骤，而只需进行必须的测量更新。

由ESMF可知，测量更新是求取预测状态椭球和观测椭球的交集[3]：

Qk-1 = Q（■k+1，Kk+1） θi = Q（■k+1|k，Kk+1|k）∩Sk   （26）

特殊地，当：

Q（■k+1|k，Kk+1|k）∩Sk        （27）

得：

Qk+1 = Q（■k+1，Kk+1） Q（■k+1|k，Kk+1|k）∩Sk        （28）

即：

Qk+1 = Q（■k+1|k，Kk+1|k）        （29）

如果满足上式（29）的条件，则表明可以省略循环滤波的测量更新步骤[3]。在实际应用中，因为符合表达上式的条件很难满足，因此通常采用如下检验方式：

[zk - g（xk+1|k）]TR-1[zk - g（xk+1|k）] ≤ η       （30）

如果参数η偏大，则忽略测量更新的几率会增大[6]，与此同时较大的边界误差会被引入，所以本优化算法会在保证算法的精度和节约算法的时间上折中考虑。当存在较小的干扰噪声时，取η = 1，此时滤波算法中的椭球中心的预测状态量被包含于集合Sk中，则可以忽略测量更新，同时确保预估性能和节省计算时间。

2.2   对滤波参数的优化

ESMF算法中包含了λk、ρk等参数，因为外定界椭球形状会被这两个参数影响[7]，所以需要选择合适的方法来优化参数。对于参数 来说，常用的优化方法为求取最小容积或最小迹椭球集合。

包含两个椭球集合的外定界椭球表达式为：

Q（a，K，ω） = Q（a1，K1，ω1）■Q（a2，K2，ω2）其中：

a = a1 + a2

K=（1+■）■K1+（1+λ）■K2，λ>0   （31）

可知，最小容积椭球等于K（椭球形状矩阵）的        最小行列式（计算上式λ最小值）：

f（λ） = det[K（λ）]        （32）

计算后的优化表达式是：

■■ = ■        （33）

其中ρλki = ρi（Ak-1Kk-1ATk-1PTk-1）、ρλki是矩阵特征值，n是状态维数。

对应的最小迹椭球为以下函数的最小值：

f（λ） = tr[K（λ）]        （34）

计算后的结果是：

λk = （■）■        （35）

已知两椭球分别是Q（a1，K1，ω1）、Q（a2，K2，ω2），则两个椭球交集的外定界椭球Qs（a，K，ω）为：

Qi（a，K，ω）=Q（a1，K1，ω1）∩Q（a2，K2，ω2）  （36）

a = a + ρ2 （ρ1K1-1 + ρ2K2-1）-1K-12（a2 - a1）        （37）

其中：ρ2，ρ2 > 0

K-1 = ρ1K-11 + ρ2K-12        （38）

ω2 = β1ω21 + β2ω22

-ω1ω2（a2-a1）T（β2K1+β1K2）-1（a2-a1）     （39）

定义β1 = 1 - ρk、β2 = ρk，则外定界椭球交集的形状矩阵是：

P-1 = （1 - ρk）K-11 + ρkK-12        （40）

因为优化难度困难和计算量大等原因，所以采用最小化ω2的上边界ω2来优化ρk：

■2k = （1 - ρk）ω2       k|k-1 + ρkγ2

-（1- ρk）ρk■≥ω2k      （41）

式中：hk是Hk的最大奇异值。

若：

ρ*k = argminsup（■2k）        （42）

令：

μk = ■        （43）

由（42）可知（41）中ρk一階和二阶导数是：

■ = γ2 - ω2k|k-1 - δTkδk■  （44）

■ = δTkδk■        （45）

分析可得：

1）当μk ≥1，ρ*k = 0

2）当μk ≤1，ρ*k = min（ε，vk）。

vk=ε;                                                   δTkδk = 0■;                                         hk = 1■（1-■）;1+μk（hk-1）≥0ε;                                         1+μk（hk-1）≤0

（46）

由式（42）结合优化ρk角度可知，计算δk决定着是否需要测量更新。另外，考虑到计算量的大小，则需要测量更新时，才会去计算hk。

3   基于ESMF的PMSM矢量控制系统

对于PMSM，在参考坐标系dq中[8]，电机的数学模型如下：

id = ■iq = ■        （47）

■ = ■        （48）

Te = 1.5p（ψf iq + （Ld - Lq）idiq）        （49）

式中id、iq，ud、uq和Ld、Lq分別是定子绕组dq轴等效电流、电压和电感;Te是电磁转矩;TL是负载转矩;ψf是转子磁链;Rs是定子绕组电阻;ω是转子机械角度;p是极对数;B是摩擦系数;J是转动惯量。

基于上面的算法原理和PMSM动态模型，建立了基于扩展集员滤波的PMSM矢量控制系统，系统框图如图1所示。

图1   基于ESMF的无位置传感器控制

4   仿真及结果分析

为了验证基于ESMF的无位置传感器的系统性能，利用Matlab/Simulink对系统进行仿真。永磁同步电机参数如表1。

表1   PMSM的参数

系统采样周期为50 μs，给定初始转速为1800 r/min，在0.15 s给定转速1400 r/min，在0.25 s给定转速1500 r/min，仿真结果如图2～图5所示。

t/s

图2   估计转速曲线与实际测量

t/s

图3   估计转速误差曲线

t/s

图4   估计位置曲线

t/s

图5 估计位置误差曲线

通过ESMF估计的转速和实际转速对比图如图2所示，估计转速与实际测量转速的曲线几乎重合;估计转速和实际转速的误差曲线如图3所示，精度比较高，当速度变化时，其误差相对均值为2%左右，而在速度稳定阶段，其误差相对均值为0.15%左右。图4是转子位置估计曲线;图5是估计位置误差曲线，可以看出位置误差波动不大，系统比较稳定。

仿真结果表明，所提出的基于ESMF算法对永磁同步电机的位置估算精度精度较高。

5   结  论

采用ESMF对PMSM矢量控制的转子转速和位置进行精确估计。仿真结果验证了ESMF在PMSM-FOC中状态的有效性，同时表明基于ESMF的PMSM-FOC闭环系统具有快速的响应特性和良好的稳定性。

参考文献

[1]    夏愉乐，李蕊，何青.一种用于非线性系统的扩展集员滤波状态估计算法[J].自动化技术与应用，2018，37（01）：1—314.

[2]    袁登科，徐延东，李秀涛.永磁同步电动机变频调速系统及其控制[M]. 北京：机械工业出版社，2015：1—9.

[3]    何青，夏愉乐，柳一琳，等.一种优化的扩展定界椭球集员滤波算法[J].长沙理工大学学报：自然科学版，2016，13（03）：70—75.

[4]    江涛，钱富才.具有双重不确定性系统的联合滤波算法[J].自动化学报，2016（4）：535—544.

[5]    何青，郑维荣.基于最优定界椭球的扩展集员滤波算法研究[J].自动化技术与应用，2015 （5）：8—11.

[6]    王魏.椭球定界算法在混合建模中的应 用研究[J].自动化学报，2014（9）：1875—1881.

[7]    杨文，侍洪波.卡尔曼一致滤波算法综述[J].控制与决策，2011（4）：481—488.

[8]    施大发，施佳，黄庆，等. 基于扩展卡尔曼滤波的PMSM无位置传感器控制[J].电源技术，2015，39（01）：161—164.