基于区间预测模型的污水处理厂传感器故障检测

柴伟　池彬彬

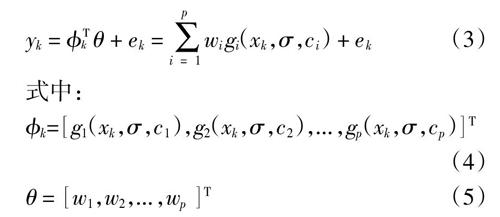
摘   要：污水处理厂配备许多传感器用于监测出水水质。传感器的正常工作与否对保证出水水质至关重要。给出了一种污水处理出水变量传感器故障检测方法。该方法根据入水和出水数据，采用径向基函数神经网络构造出水变量预测模型;使用参数线性集员辨识算法得到网络输出权值的集合描述，从而使预测模型能够给出出水变量的置信区间;以此置信区间为基础获得传感器的故障检测策略。由于置信区间描述了出水变量的存在范围，当传感器测量值超出置信区间，则可推断传感器发生故障。此外，在设计传感器故障检测策略时还考虑了污水处理过程异常的影响。实验结果证实所提方法的有效性。

关键词：污水处理;传感器;故障检测;集员辨识;区间预测

中图分类号：TP277                                             文献标识码：A

Fault Detection of Sensors in Wastewater Treatment

Plants Using Interval Predictor Models

CHAI Wei1，2？覮， CHI Bin-bin1，2

（1. Faculty of Information Technology，School of Automation，Beijing University of Technology，Beijing 100124，China;

2. Beijing Key Laboratory of Computational Intelligence and Intelligent Systems，Beijing 100124，China）

Abstract：A wastewater treatment plant（WWTP） is equipped with a number of sensors for monitoring the quality of the effluent. The normal operation of the sensors is critical to ensuring the quality of the effluent. This paper presents a fault detection method for sensors measuring the effluent variables in the WWTP. According to the available influent and effluent data，the radial basis function neural network is used to construct the predictor models for the effluent variables. Linear-in-parameters set membership identification algorithm is used to obtain a description of the uncertain set of the vector representing the output weights of the neural network，so that the predictor model can give a confidence interval of the effluent variable. Basing on this confidence interval，the sensor fault detection strategy is obtained. Since the confidence interval describes the existence range of the effluent variable，when the measurement result exceeds the confidence interval，it can be inferred that the sensor has been faulty. Besides，the influence of abnormal operation of the WWTP is considered in designing the sensor fault detection strategy. The experimental results confirm the effectiveness of the proposed method.

Key words：wastewater treatment;sensor;fault detection;set membership identification;interval prediction

污水处理作为保护环境的重要措施得到广泛关注。日益严格的出水排放标准要求污水处理厂配备先进的自动控制系统，而控制系统的有效运行依赖于传感器的可靠性。传感器故障将导致能耗增加与出水水质下降。尽管传感器冗余可以提高可靠性，但也会带来成本的增加。所以，为了有效降低故障的消极影响，需要在污水处理厂配置传感器故障检测与诊断系统[1]。

目前针对污水处理过程传感器故障检测与诊断方面的研究已经取得较丰富的成果。文[2]根据机理模型设计状态观测器对执行器和传感器故障进行检测与诊断。为了克服机理模型精度不高的缺陷，文[3，4]基于过程数据采用多元统计方法，如主元分析（PCA），对传感器故障进行检测与诊断。PCA要求过程数据在不同时刻统计独立，该假设不适用于具有动态特性的污水处理过程，因为数据具有自相关性。所以，在实际应用中需要对PCA进行改进。为了克服该缺点，具有自回归滑动平均结构的非线性黑箱模型[5-8]被用于污水处理传感器故障检测。该类方法通过检验代表传感器正确结果的模型输出与传感器测量结果之差（残差）实现故障检测。文[5]采用多层前馈神经网络建立氮预测模型;文[6]采用具有进化能力的T-S模糊模型建立曝气系统中空气流量和氧浓度以及入水氨氮浓度预测模型;文[7]采用归纳置信预报建立出水生化需氧量（BOD）區间预测模型，对BOD在线分析仪进行校准和故障检测;文[8]采用高斯过程回归建立关于污水流量和氨浓度区间预测模型。相比文[5，6]，文[7，8]对残差阈值进行了更合理的设置。另外，文[9-11]研究传感器故障对反馈控制系统性能的影响以及传感器故障检测与诊断和容错控制方法。

从前面分析可见，文[5-8]方法可以克服文[2]和文[3，4]方法的不足。该类方法基于残差的统计特性设置故障检测阈值。然而污水处理过程机理复杂，并且存在时变、干扰和测量噪声等诸多不确定因素，因此残差的统计特性较难获得，文[5-8]方法的性能可能会受到影响。为了克服此问题，本文给出一种新的污水处理出水变量传感器故障检测方法。该方法借鉴文[12-16]的思想，将集员辨识与径向基函数（RBF）神经网络相结合建立出水变量区间预测模型，置信区间是残差阈值的一种表达形式，此区间的计算不需要任何变量的统计特性，从而该方法相比文[5-8]更具实用性。此外，还将考虑污水处理过程异常对传感器故障检测的影响以及相应的应对措施。

1   污水处理厂模型

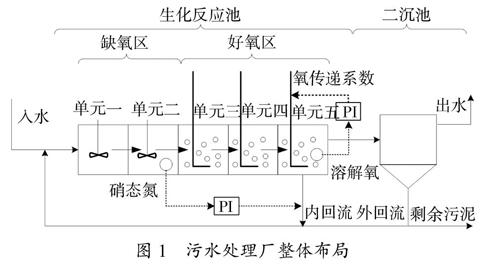
采用国际水协与欧洲科学与技术合作组织联合開发的污水处理基准仿真模型（BSM1，见http：//www.benchmarkwwtp.org）测试传感器故障检测方法。污水处理厂采用典型的前置反硝化脱氮工艺（如图1），由一个生化反应池和一个二沉池串联构成。在生化反应池中，前两个单元为缺氧但完全混合的，各单元容积为1000 m3;后三个单元是好氧的，各单元容积为1333 m3。二沉池面积1500 m2，总高度4 m，分为10层，入水口在从底部数第6层。该水厂在干燥天气下平均每日处理18446 m3污水，其中化学需氧量（COD）平均浓度为300 g/m3，剩余污泥平均每日排放385 m3。该水厂通过内外两个回流提供硝态氮和补充微生物。生化反应池和二沉池分别通过活性污泥模型1号和双指数沉降速率方程描述。

图1   污水处理厂整体布局

2   污水处理厂传感器故障检测方法

2.1   出水变量区间预测模型

2.1.1   RBF神经网络

RBF神经网络具有拓扑结构简单和逼近能力强大的特点。它包括输入层、隐含层和输出层，可以表示为

式中：y∈R和x∈RQ分别是网络的输出和输入，在出水变量预测模型中分别代表出水变量和入水变量，Q表示入水变量的个数;gi（x，σ，ci）为神经网络第i个隐含层节点的输出，ci∈RQ和σ∈R分别为中心和宽度; wi∈R为线性输出权值，p为隐含层节点个数。RBF神经网络的隐单元基函数

式中‖·‖表示欧式范数。

2.1.2   出水变量置信区间计算

以水厂入水和出水变量分别作为RBF神经网络的输入和输出，建立出水变量区间预测模型。为了建立模型，首先需要获取水厂入水和出水数据。记用于建模和预测的数据集分别为D1={xk，yk}N    k=1和D2={xk，yk}L        k=N+1。这里xk和yk分别表示污水处理厂k时刻入水和出水变量。

采用聚类算法[17]确定RBF神经网络的中心ci和宽度σ。之后，得到关于输出权值wi的线性方程

这里假设建模误差ek为有界误差，即|ek|≤ρ。因为它是与神经网络逼近能力有关而统计特性难以确知的有界量。基于此假设，本文采用集员辨

识[18-20]算法估计神经网络的输出权值，从而使预测模型可以给出出水变量的置信区间。

由样本数据D1={xk，yk}N    k=1、误差的有界假设|ek| ≤ρ以及式（3）可以得到

（6）

N个Sk的交集可得到一个凸多面体PN■Rp，即PN = ∩N    k=1Sk。这里PN称为权值向量θ的不确定集。

以权值向量的不确定集为基础可获得出水变量的置信区间，主要方法有如下三种。

方法1：根据θ∈PN、式（3）和误差有界假设|ek| ≤ρ，可得到出水变量yk的置信区间

式中：

置信区间式（7）和（8）可通过线性规划算法得到。

方法2：通过集员辨识的盒子外界算法[18]获得一个包含权值不确定集PN的盒子

盒子BN可通过求解如下2p个线性规划问题得到

根据θ∈PN、式（3）、误差有界假设|ek|≤ρ以及 PN？哿BN，可得到出水变量yk的置信区间

式中：

方法3：通过集员辨识的椭球外界算法[21，22]获得一个包含权值不确定集PN的椭球

式中：εN∈ RP是椭球EN的中心，γN∈Rp× p是一个表征椭球形状和大小的正定矩阵。这里给出文[21]中的椭球外界算法，其改进形式见文[22]。

算法1

初始化：置ε0 = 0，γ0 = η-1I，I为单位阵，η取小的正数，如10-5。

递推：对k = 1，2，…，N

步骤1. 计算

步骤2. 如果αk≤p（ρ2 - vk2），则置εk= εk-1，γk = γk-1。否则，计算

式中：

上面的qk为如下方程的正实根

（p - 1）αk2qk2 +（（2p-1）ρ2 - αk + v2k）αkqk +

ρ2（p（ρ2-v2k）- αk） = 0     （20）

步骤3. 如果k < N，则k增1并返回步骤1。

根据θ∈ PN、式（3）、误差有界假设|ek| ≤ρ以及PN？哿BN，可得到出水变量yk的置信区间

yk∈■Ek- ρ，■Ek+ ρ，k ≥ N + 1      （21）

式中：

即采用方法1所得置信区间保守性最低，但该方法的计算成本也最高。此外，不难发现，置信区间源于有界误差假设|ek| ≤ρ，它的推导过程不涉及任何变量的统计特性。

2.2   传感器故障检测策略

本节基于出水变量区间预测模型提出污水处理厂传感器故障检测方法。假设入水变量数据可以准确获取并且不会出现多个出水变量传感器同时发生故障的情况。

1.假设污水处理过程不出现异常。已建立好的区间预测模型根据入水变量xk计算出水变量yk的置信区间。由于置信区间描述了水厂在正常运行条件下出水变量yk的存在范围，对某k时刻，如果有yk的测量值不在它的置信区间之内，则可推测测量yk 的传感器发生故障。

2.假设污水处理过程会出现异常。建立M个出水变量区间预测模型。这些模型根据入水变量x（i）k分别同时给出出水变量y（i）k的置信区间，i = 1， …，M。置信区间描述了水厂在正常运行条件下出水变量的存在范围。对某k时刻，如果有且仅有一个出水变量测量数据y（i*）k不在它的置信区间之内，则可推测第i*个出水变量传感器发生故障，如果出现多个出水变量测量数据不在各自的置信区间之内，则可推断污水处理过程出现异常。

注记1. 权值不确定性使模型输出■k为区间[■k，yk]（略去上标P、B、E），k≥N+1 。若定义模型输出■k = ■（yk+ yk）（区间中心）以及残差rk = yk - ■k，则

（26）

上式表明置信区间是残差阈值的一种等价形式。

3   实验

实验数据基于第1节所介绍的BSM1获得。采用晴好天气入水文件，该文件包括采样间隔为15 min的14 d污水处理厂实测数据。建立两个出水变量模型，模型的输入个数均为3，输入为入水流量、COD和总悬浮固体（TSS），模型的输出分别为出水COD和BOD。水厂仿真完成之后共获得1344对入水和出水数据，即L = 1344。将前7天数据用于模型建立，共672对，即N=672;后7天数据用于模型预测。

在建模之前，需要先对输入数据（式（3）中的xk）进行归一化处理。采用文中三种方法建立出水变量区间预测模型，其中方法3基于文[22]中的算法并重复处理数据200次以降低外界描述保守性。对于出水COD模型，神经网络隐节点数p、宽度σ以及建模误差界ρ分别为5、3.4和2.117 g/m3;对于出水BOD模型，三个参数分别为5、3.2和0.2324 g/m3。

三種方法的性能比较如表1和表2所示，其中耗时1为计算权值不确定集外界所需时间，耗时2为计算置信区间所需时间。计算机CPU为Intel（R） Core（TM）2 Duo，内存为2G，软件为Matlab 6.1。可以看出，方法3可在结果的保守性和计算成本之间取得很好的折中，实际应用价值很大，而方法1可以获得保守性最低的结果，但使用前提是运行时间能够忍受。这里，方法1大约需要1 s的时间预测下一时刻出水变量的置信区间，对于数据采样间隔15 min来说，能够满足实时性要求。

表1   方法的性能（COD模型）

表2   方法的性能（BOD模型）

图2示出采用方法1获得的出水COD和BOD置信区间。图中实线为测量值，虚线为区间上下界（式（7））。可见，测量值全部落入置信区间中。

时间/d

（a）

时间/d

（b）

图2   出水变量置信区间： （a） COD;（b） BOD

这里考虑三种故障场景：1.假设污水处理过程不会出现异常，出水COD传感器精度从第10天开始变差，测量结果被服从均值为0、方差为1的正态分布的噪声污染;2. 假设污水处理过程会出现异常，出水BOD在线分析仪在第10、11天的测量结果为真实值的70%;3. 污水处理厂从第10天开始外回流流量为正常值的一半（尽管出水COD和BOD浓度下降，但出水氨氮浓度严重超标）。

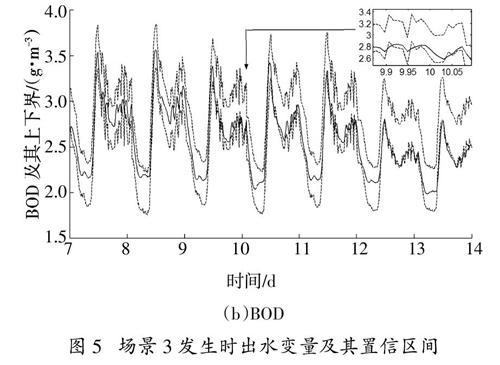
当场景1发生时，出水COD传感器测量值越出置信区间，如图3所示，此时可推断出水COD传感器发生故障。当场景2发生时，出水COD情况仍如图2（a）所示，而出水BOD情况如图4所示，此时可推断出水BOD在线分析仪发生故障。当场景3发生时，两个出水变量测量值均越出置信区间，如图5所示，此时可推断污水处理过程出现异常。

时间/d

图3   场景1发生时出水COD及其置信区间

时间/d

图4   场景2发生时出水BOD及其置信区间

时间/d

（a）COD

时间/d

（b）BOD

图5   场景3发生时出水变量及其置信区间

4   结   论

提出了一种新的污水处理出水变量传感器故障检测方法。该方法将集员辨识与RBF神经网络相结合建立出水变量区间预测模型，并基于出水变量置信区间获得传感器的故障检测策略。置信区间的计算不需要任何变量的统计特性，从而本文方法相比文[5-8]更具实用性。此外，在设计传感器故障检测策略时还考虑了污水处理过程异常的影响。

参考文献

[1]    SCHRAA O，TOLE B，COPP J B. Fault detection for control of wastewater treatment plants[J]. Water Science and Technology，2006，53（4-5）：375—382.

[2]    FRAGKOULIS D，ROUX G，DAHHOU B. Detection，isolation and identification of multiple actuator and sensor faults in nonlinear dynamic systems：Application to a waste water treatment process[J]. Applied Mathematical Modelling，2011，35（1）：522—543.

[3]    LEE C，CHOI S W，LEE I B. Sensor fault diagnosis in a wastewater treatment process[J]. Water Science and Technology，2006，53（1）：251—257.

[4]    TAO E P，SHEN W H，LIU T L，et al. Fault diagnosis based on PCA for sensors of laboratorial wastewater treatment process[J]. Chemometrics and Intelligent Laboratory Systems，2013，128：49—55.

[5]    CACCAVALE F，DIGIULIO P，IAMARINO M，et al. A neural network approach for on-line fault detection of nitrogen sensors in alternated active sludge treatment plants[J]. Water Science and Technology，2010，62（12）：2760—2768.

[6]    DOV？譕AN D，LOGAR V，？譒KRJANC I. Implementation of an evolving fuzzy model （eFuMo） in a monitoring system for a waste-water treatment process[J]. IEEE Transactions on Fuzzy Systems，2015，23（5）：1761—1776.

[7]    LIU Y Q，HUANG D P，LI Y. Development of interval soft sensors using enhanced just-in-time learning and inductive confidence predictor[J]. Industrial and Engineering Chemistry，2012，51（8）：3356—3367.

[8]    SAMUELSSON O，BJ？魻RK A，ZAMBRANO J，et al. Gaussian process regression for monitoring and fault detection of wastewater treatment processes[J]. Water Science and Technology，2017，75（12）：2952—2963.

[9]    ZUMOFFEN D，BASUALDO M. Improvements in fault tolerance characteristics for large chemical plants：1. Waste water treatment plant with decentralized control[J]. Industrial & Engineering Chemistry Research，2008，47（15）：5464—5481.

[10] CARLSSON B，ZAMBRANO J. Fault detection and isolation of sensors in aeration control systems[J]. Water Science and Technology，2016，73（3）：648—653.

[11]  BELCHIOR C A C，ARA？譈JO R A M，SOUZA F A A，et al. Sensor-fault tolerance in a wastewater treatment plant by means of ANFIS-based soft sensor and control reconfiguration[J]. Neural Computing and Applications，2018，30（10）：3265—3276.

[12]  柴偉，孙先仿. 一种非线性系统集员辨识算法[J]. 北京航空航天大学学报，2005，31（11）：1237—1241.

[13]  CHAI Wei，QIAO Jun-fei. Non-linear system identification and fault detection method using RBF neural networks with set membership estimation[J]. International Journal of Modelling，Identification and Control，2013，20（2）：114—120.

[14]  CHAI Wei，QIAO Jun-fei. Passive robust fault detection using RBF neural modeling based on set membership identification[J]. Engineering Applications of Artificial Intelligence，2014，28：1—12.

[15]  柴伟，纪镐南. 污水处理出水BOD区间预测建模[J]. 哈尔滨工业大学学报，2018，50（2）：71—76.

[16]  CHAI Wei，GUO Long-hang，LI Xue-meng，et al. Interval prediction of effluent TP for wastewater treatment plants[C]. Proceedings of 3rd IEEE Conference on Control Technology and Applications. 2019：511—516.

[17]  BEZDEK J C. Pattern recognition with fuzzy objective function algorithms[M]. New York：Plenum Press，1981.

[18]  MILANESE M，VICINO A. Optimal estimation theory for dynamic systems with set membership uncertainty：An overview[J]. Automatica，1991，27（6）：997—1009.

[19]  CHAI Wei. Nonlinear set membership identification by locally linear embedding[J]. International Journal of Innovative Computing，Information and Control，2014，10（6）：2193—2207.

[20]  柴伟，纪镐南. 基于等距映射的非线性系統集员参数估计[J]. 电子科技大学学报，2018，47（2）：203—208.

[21]  FOGEL E，HUANG Y F. On the value of information in system identification-bounded noise case[J]. Automatica，1982，18（2）：229—238.

[22]  BELFORTE G，BONA B. An improved parameter identification algorithm for signals with unknown but bounded errors[C]. Proceedings of the 7th IFAC/IFORS Symposium on Identification and System Parameter Estimation. 1985：1507—1511.