带有稀疏执行器故障的事件触发网络化系统容错控制
关燕鹏 张文婷 平国楠


摘 要:针对一类具有事件触发信息传输机制的网络化控制系统,对系统故障执行器个数进行稀疏约束,研究系统在有限个执行器失效情况下的指数稳定及控制器设计问题。将系统故障执行器个数的约束转化为对控制器增益矩阵行的势约束,利用混合整数方法来解决这类稀疏约束的容错控制问题。在此基础上,利用Lyapunov泛函方法,得出闭环系统在有限个执行器失效情况下系统呈指数稳定的充分条件以及具有行稀疏约束的控制器设计方法。最后,通过一个飞行控制系统的数值仿真实例验证所提控制方法的可行性和有效性。
关键词:网络化控制系统;事件触发传输机制;执行器故障;稀疏约束;容错控制
中图分类号:TP273 文獻标识码:A
Fault-tolerant Control of Event-triggered Networked
System Based on Sparse Actuator Fault
GUAN Yan-peng?覮,ZHANG Wen-ting,PING Guo-nan
(Department of Automation,Shanxi University,Taiyuan,Shanxi 030006,China)
Abstract:For a class of networked control systems with event-triggered information transmission mechanism,the number of fault actuators is sparsely constrained,and the exponential stability and controller design of the system with a limited number of actuator failures are studied. The contribution is to convert the number of fault actuators to a cardinality constraint on the controller gain matrix. The mixed integer programming is used to solve this kind of sparse constraint problem. By using the Lyapunov functional method,we obtained a sufficient condition for the closed loop system to be exponentially stable with a limited number of actuator failures and a controller design method with row sparse constraints is also presented. Finally,the effectiveness of the proposed method is verified by a numerical simulation example about a flight control system.
Key words:networked control systems;event-triggered transmission mechanism;actuator failure;sparse constraint;fault-tolerant control
控制系统是由被控对象、控制器、传感器、执行器以及计算机软硬件组成的闭环系统,系统的各个环节都有可能发生故障,据统计,80%以上的控制系统故障都是由执行器或传感器发生故障所导致,所以在设计系统时如果不考虑控制系统的某些部件(如传感器或执行器等)在其运行过程中发生故障或失效对系统的影响,那么一旦出现故障就有可能导致系统性能下降或系统不稳定,甚至导致整个系统崩溃,由此带来的损失是无法估量的,所以容错控制理论正成为控制理论与控制工程的研究热点[1-10]。近几年,许多研究者都在进行故障容错控制方面的研究[11-17]。例如文[11]研究了一类具有干扰和执行器故障的不确定大规模互联系统的分散自适应容错控制问题,故障类型包括卡滞、停电和失效。文[12]针对一类具有随机执行器故障的网络化T-S模糊系统,提出一种能有效减少数据传输量的事件触发机制。文[13]研究一类具有输出扰动的离散时间切换系统的执行器故障检测问题。文[14] 研究了串联同轴管道风扇飞机在系统不确定,不匹配扰动以及执行器饱和情况下的鲁棒自适应容错控制问题。文[15]针对一类具有执行器故障的非线性系统,提出基于线性矩阵不等式的一体化鲁棒主动容错控制器设计方法。
目前文章中执行器故障的表现形式主要分以下两类,第一类为执行器故障情况随时间而改变,如文[16]针对一类带有执行器故障的不确定线性系统,设计带有参数更新律的自适应H无穷容错控制器,其执行器故障模式为uF(t) = u(t) + F(t),F(t)为其时变故障向量;第二类为引入故障开关阵F = diag{f1,f2,…fn},fi值为1,代表第 个执行器正常,值为0,代表第i个执行器失效。如文[17]针对一类网络诱导时滞模型,设计状态反馈形式的自适应容错控制器,执行器故障模式表示为uF(t)=(1-ρ)u(t),其中ρ = diag{ρ1,ρ2,…,ρn},ρi∈{0,1]是未知常数,ρi = 1和ρi = 0分别代表第i个执行器故障或正常。
容錯控制可分为主动容错和被动容错两大类别。主动容错控制需要在线提取故障诊断信息,所设计的控制器结构和参数均需要在线调整,目前应用最为广泛的主动容错方法为自适应容错控制,此方法可以有效应对各种故障类型,在线动态弥补故障情况,进而设计出期望的系统性能,但自适应率对于故障的估算通常会消耗大量的计算信息和计算时间,且自适应系统自身也存在非线性特性,而这些问题均会削弱系统的容错效果。被动容错即设计一个控制器,其结构和参数都是恒定的,不需要在线调整,在设计系统之前就已经考虑了系统可能发生的故障,系统不包含故障检测和隔离单元,具有易于实现的优点,但同时也增加了系统的保守性,鲁棒容错控制就是一种典型的被动容错方法。
值得指出的是,无论是主动容错还是被动容错,目前所提出的系统故障模型大多为传感器或执行器发生故障,且随机设定故障传感器或执行器,均没有考虑对传感器或执行器故障个数进行稀疏约束的问题,针对这类问题,本文对一类带有稀疏执行器故障的事件触发网络化系统进行容错控制,将故障执行器个数的约束转化为对系统控制器增益矩阵行的势约束,利用混合整数方法来解决这类带有稀疏约束的容错控制问题,结合Lyapunov泛函方法以及矩阵变换,得到使系统呈指数渐近稳定的充分条件以及具有行稀疏约束的控制器设计方法,并通过数值例子证明此方法的有效性。
2 问题描述
考虑如下一类线性系统:
(t) = Ax(t) + Bu(t) y(t) = Cx(t) (1)
其中:x(t)∈Rn为系统状态向量,u(t)∈Rm为系统的控制输入向量,y(t)∈RT为被控输出量,A、B、C为适当维数的常数矩阵,系统初始条件为x(0) = x0。在本文中,我们利用采样周期为h的采样器来测量状态x(t),为了充分利用网络资源,减少冗余数据的传输和计算,并非所有测量状态都将用于反馈控制,为此,我们提出一种基于事件触发的信息传输机制来确定状态测量值是否被传递给控制器,以用于控制输入计算。其系统结构图如图1所示:
图1 事件触发网络系统结构示意图
系统的采样时刻序列为{kh}∞1,而被传输的数据采样时刻序列为{tkh}∞1,为了更好地说明问题,不考虑信号采样和传输过程中的时延问题,但对于具有时延的网络控制系统,所提出的方法同样适用。在当前采样状态值x(kh)与最近一次被传输的采样状态值x(tkh)之间的误差突破事件触发阀值条件时,当前采样状态值才可被传输,本文所采用的事件触发条件如式(2)所示:
[x(kh) - x(tkh)]TΦ[x(kh) - x(tkh)] <
δxT(tkh)Φx(tkh) (2)
其中,Φ > 0为加权矩阵,δ∈(0,1)为事件阀值参数。那么时间序列{tkh}∞1的产生可表示为如下形式:
tk+1h = minkh > tkh|[x(kh) - x(tkh)]TΦ[x(kh) - x(tkh)] ≥ δxT(tkh)Φx(tkh)
(3)
选取状态反馈控制律,其形式为:
u(t) = Kx(tkh),t∈[tkh,tk+1h] Cardrow(K)≤κr
(4)
Km×n是待求的控制器增益矩阵,Cardrow(K)≤κr表示矩阵的非零行个数不超过κr个,全零行的个数不少于 m - κr个,1≤κr≤m,即意味着系统故障执行器个数不少于m-κr个。换言之,当控制器增益矩阵非零行个数为κr时,系统需要选取κr个执行器保持工作以维持系统所需的性能。当κr值越小即意味着系统在保持一定性能指标的前提下所需执行器的个数越少,系统的容错能力越强,从而可以节省网络资源,降低成本。在区间t∈[tkh,tk+1h)内,定义:
rk,ih=tkh+ih,i∈Ω:=0,1,2,…,tk+1-tk-1(5)
e(rk,ih) = x(rk,ih) - x(tkh) (6)
当t∈[tkh,tk+1h),i∈Ω时,令η(t) = t - rk,i h,那么,0≤η(t) x(tkh)=x(t-η(t))-e(rk,ih),t∈[tkh,tk+1h] (7) 根据式(4)可将带有执行器故障的事件触发闭环系统表示为: (t) = Ax(t) + BKx(t - η(t) -BKe(rk,i)) y(t) = Cx(t),t∈[tkh,tk+1h] (8) Cardrow(K) ≤ κr 目标是设计如式(4)所示的行稀疏状态反馈控制器增益矩阵K,将系统故障执行器个数的约束转化为对控制器增益矩阵行的势约束,使得闭环系统(8)在有限个执行器失效的情况下达到指数渐近稳定。 3 主要结果 在本节中,将给出闭环系统(8)呈指数渐近稳定的充分条件,以下引理将被用于主要结果的推导: 引理1[18]:Y,R为适当维数的矩阵,R>0,存在常数h>0,η(t)∈[0,h),且可积函数■(t):[-h,0]→Rn,如果矩阵R YYT R > 0成立,那么不等式(9)即可成立。
-h■■(v)R■(v)dv ≤ ξT(t)πξ(t) (9)
其中
ξ(t) = x(t)x(t - η(t)) x(t - h),π =-R R + Y -Y * -2R-Y-YT R+Y * * -R
(10)
*表示对称矩阵中的对称项。
实现对控制器增益矩阵行的势约束是关键部分,根据文[19]中关于向量零范数等效转换的论述,本文对矩阵的行稀疏约束进行如下处理。
引理2[19]:对于一个矩阵K∈Rm×n,假设矩阵 中各元素绝对值的最大值不超过M,即矩阵满足条件‖K‖≤M,M是一个正数,如果不等式Cardrow(K)≤κr成立,则存在一个二进制序列bi∈{0,1},i = 1,2,…,m,使得不等式(11)成立。
K(i,j) ≤ M(1 - bi),■bi ≥ m - κr (11)
证明:必要性:因为Cardrow(K)≤κr,其代表矩阵K非零行的个数r(K)≤κr,所以m-r(K)≥m-κr。定义一个二进制序列bi,当矩阵K第i行为非零行,bi值为0,当矩阵K第i行为全零行,bi值为1,则容易验证■bi = m-r(K)≥m-κr。又因为‖K‖≤M,所以bi为0时,K(i,j)≤M,bi为1时,K(i,j) = 0,所以,K(i,j)≤M(1 - bi)。
充分性:由于K(i,j)≤M(1 - bi)且bi是一个二进制序列,所以当bi为1时,可使矩阵K第i行为全零行,那么■bi即代表矩阵K全零行的个数。因为■bi ≥ m-κr,则表明矩阵K全零行的个数不少于m-κr个,也表明矩阵K非零行的个数不多于κr个,即Cardrow(K)≤κr,证毕。
通过这样的方法将稀疏约束条件转化为混合整数规划问题,利用Matlab中intlinprog函数即可有效地解决这类求解问题。
下面将给出闭环系统(8)的稳定性条件,并利用此条件给出容错控制器的设计方法。
定理1:给定的标量α > 0,σ > 0,δ∈(0,1),h > 0以及一个满足1≤κr≤m的整数,如果存在实矩阵P > 0,Q > 0,R > 0,以及具有适当维数的矩阵Y,K,且存在一个标量M > 0以及一个二进制序列bi∈{0,1},i = 1,2,…,m,使得下列不等式成立:
(13)
其中Γ11 = AP + PAT + 2αP + Q - e-2αhR,则带有稀疏执行器故障的事件触发网络控制系统在衰减速率为α的情况下呈指数稳定,且K = KP-1,并满足条件Cardrow(K)≤κr。
证明:选取如下李雅普诺夫函数:
V(t,x(t)) = xT(t)Px(t)
+ ■e2α (v - t)xT(v)Qx(v)dv
+ h■■e2α (s- t)xT(s)R■(s)dsdv (14)
其中P、Q、R为正定矩阵。
对李雅普诺夫函数关于时间t求导可得:
■(t,x(t)) = 2xT(t)P■(t)
+ ■2αe2α (v - t)xT(v)Qx(v)dv
+ xT(t)Qx(t) + h2■T(t)R■(t)
+ h■■-2αe-2α (s - t)■T(s)R■(s)dsdv
- h■e2α (v - t)■T(v)R■(v)dv (15) 將式(15)加上2αV(t,x(t)),可得:
■(t,x(t)) + 2αV(t,x(t))=
2xT(t)P■(t) + 2αxT(t)Px(t) + xT(t)Qx(t)+
h2■T(t)R■(t) - h■e2α (v - t)■T(v)R■(v)dv
(16)
根据引理1可知:
-h■e2α (v - t)■T(v)R■(v)dv ≤ e-2αhξT(t)πξ(t)
(17)
其中,
ξ(t)=x(t)x(t - η(t))x(t - h),π=-R R + Y -Y * -2R-Y-YT R+Y * * -R
所以式(16)可表示为:
■(t,x(t)) + 2αV(t,x(t))
≤2xT(t)P[Ax(t) + BKx(t - η(t))-BKe(rk,i)]+
2αxT(t)Px(t) + xT(t)Qx(t) + h2xT(t)Rx(t)+
e-2αhξT(t)πξ(t) (18)
由事件触发条件式(2)可知:
eT(rk,i)Φe(rk,ih)
< δ[x(t-η(t))-e(rk,ih)]TΦ[x(t-η(t))-e(rk,ih)]
其等价于:
[xT(t - η(t)) eT(rk,ih)] δΦ -δΦ-δΦ (δ-1)Φx(t-η(t)) e(rk,ih)>0
(19)
结合式(18)-(19),可得如下不等式:
(t,x(t))+2αV(t,x(t))≤φ(t)(Υ+h2MTRM)φ(t)
(20)
其中,
φ(t) = ξ(t)e(rk,ih),M = [A BK 0 -BK]
Υ = Υ11 PBK+e-2αh(R + Y) -e-2αhY -PBK * δΦ-e-2αh(2R + Y + YT) e-2αh(R + Y) -δΦ * * e-2αhR 0 * * * (δ - 1)Φ
且Υ11 = PA + ATP + 2αP + Q - e-2αhR,结合Schur补定理,可得到系统在衰减速率为α的情况下呈指数渐近稳定的一个充分条件:
R YYT R ≥ 0
Ξ = Ξ11 PBK+e-2αh(R + Y) -e-2αhY -PBK hAT * δΦ-e-2αh(2R + Y + YT) e-2αh(R + Y) -δΦ hKTBT * * e-2αhR 0 0 * * * (δ - 1)Φ -hKTBT * * * * -R-1<0
(21)
其中Ξ11 = PA + ATP + 2αP + Q - e-2αhR。
基于以上對系统稳定性的分析,可通过矩阵变换来获得系统的控制器增益矩阵。对矩阵Ξ两边均乘以对角阵{P-1,P-1,P-1,P-1,I},令P = P-1,Q = P-1QP-1,R = P-1RP-1,K = KP,Y = P-1YP-1,Φ = P-1ΦP-1,可得式(22),
Γ11 B■+e-2αh(■+■) -e-2αh■ -B■ h■AT * δ■-e-2αh(2■+■+■T) e-2αh(■+■) -δ■ h■TBT * * e-2αh■ 0 0 * * * (δ - 1)■ -h■TBT * * * * -R-1<0
(22)
同時得到系统的控制器增益矩阵K = KP-1。
由于矩阵中存在非线性项-R-1,且-R-1=-[P-1 RP-1]-1,为了便于使用Matlab工具箱进行求解,可将其进行如下转换:
由于P,R为正定矩阵,必然存在参数σ使得式(23)成立,
(■ - σ■)■-1(■ - σ■) ≥ 0 (23)
将其展开后可得:
-PR-1■ ≤ -2σ■ + σ2■ (24)
所以-R-1可用-2σ■ + σ2R来替代,由此可得式(13),若式(13)成立,则式(25)即可成立。
■(t,x(t)) + 2αV(t,x(t)) < 0 (25)
结合引理2可知,若式(26)成立,则控制器增益矩阵K满足稀疏约束条件,即Cardrow(K)≤κr。
■(i,j)≤M(1-bi),■bi≥m-κr (26)
由此说明,基于事件触发的稀疏执行器故障网络化系统在衰减速率为α的情况下呈指数渐近稳定,控制器增益矩阵K = KP-1,且满足条件Cardrow(K)≤κr,证毕。
4 仿真实例
为了证明所提方法的有效性,以波音747的飞机横向动力学模型为仿真算例,其线性化模型可以描述为[20]:
■(t) = Ax(t) + Bu(t) x(t) = [β,yr,p,?准]T (27)
其中,β代表侧滑角,yr代表偏航率,p为滚转率,?准为滚转角,初始条件为x(0) = [0.5,-0.8,-1, 0.8]T,u是代表三个控制信号的控制向量u = [u1,u2,u3],分别代表三个方向舵的伺服控制系统,在40000英尺水平飞行和前进速度为774英尺/秒(马赫0.8)的情况下,波音747横向动力学矩阵如下:
A = -0.0558 -0.9968 0.0802 0.0415 0.598 -0.115 -0.0318 0 -3.05 0.388 -0.465 0 0 0.0805 1 0
B = 0.00729 0.01 0.05 -0.475 -0.5 -0.3 0.153 0.2 0.1 0 0 0
選择采样周期h = 0.1s,指数衰减率α = 0.01,增益矩阵K各元素绝对值的最大值不超过105,即M = 105,事件触发阀值参数δ = 0.2,以κr≤2为例,利用Matlab中的LMI工具箱求解线性矩阵不等式(13),可求得增益矩阵K为:
K = -0.21759 0.64001 0.088754 0.058592-0.21621 0.64755 0.089534 0.058649 0 0 0 0
事件触发权重矩阵Φ为:
Φ= 0.0032619 -0.0048638 -0.00050473 -0.00067897 -0.0048683 0.018229 0.0027539 0.0015164-0.00050473 0.0027539 0.00049883 0.00020134-0.00067897 0.0015164 0.00020134 0.00018582
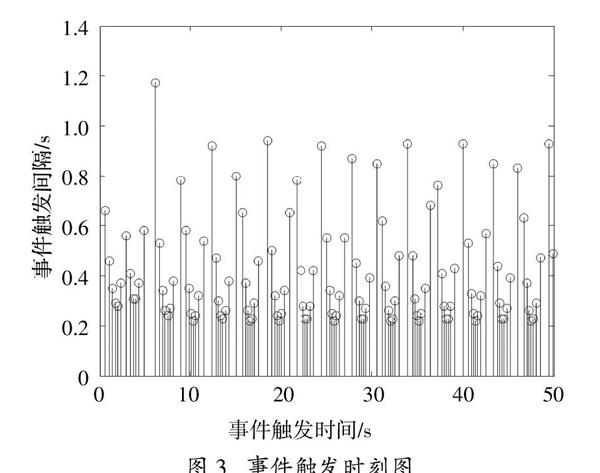
在运行时间T = 50 s情况下,系统状态响应曲线如图2所示,事件触发时刻如图3所示:
图3 事件触发时刻图
由以上仿真结果可知,Cardrow(K) = 2,即代表系统控制器增益矩阵K有两行为非零行,也可代表系统有一个执行器出现故障,其余两个均正常。根据图2可知,在一个执行器出现故障的情况下,系统仍可保持稳定,从而说明系统需选取两个执行器保持工作以维持系统所需的性能,也可说明系统具有一定的容错能力。在系统仿真过程为50秒的情况下,被传输的采样状态共120次,与采样次数相比数据传输量明显降低,表明带有稀疏执行器故障的事件触发网络化系统可有效节省网络资源,达到降低成本的目标。
5 结 论
提出了一种针对网络化系统稀疏执行器故障的容错控制设计方法。通过对控制器增益矩阵行的势约束实现对系统故障执行器个数的稀疏约束,利用混合整数的方法解决这类稀疏约束问题,并结合李雅普诺夫泛函方法得出系统在事件触发条件下呈指数渐近稳定的充分条件以及具有行稀疏约束控制器的设计方法,最后通过一个实际数值仿真例子验证了所提方法的有效性。
参考文献
[1] YE S,ZHANG Y,WANG X. Fault-tolerant control for a class of uncertain systems with actuator faults[J]. Tsinghua Science & Technology,2010,15(2):174—183.
[2] WU L. Robust adaptive fault-tolerant control for linear systems with actuator failures and mismatched parameter uncertainties[J]. Iet Control Theory & Applications,2014,8(6):441—449.
[3] XU Y,TONG S,LI Y. Prescribed performance fuzzy adaptive fault-tolerant control of non-linear systems with actuator faults[J]. Iet Control Theory & Application,2014,8(6):420—431.
[4] WANG Z,RODRIGUES M. Actuator fault estimation observer design for discrete-time linear parameter varying descriptor systems[J]. International Journal of Adaptive Control & Signal Processing,2015,29(2):242—258.
[5] DEFOORT M,VELUVOLU K. Adaptive sensor and actuator fault estimation for a class of uncertain Lipschitz nonlinear systems[J]. International Journal of Adaptive Control & Signal Processing,2016,30(2):271—283.
[6] LI Y,YANG G. Robust fuzzy adaptive fault-tolerant control for a class of nonlinear systems with mismatched uncertainties and actuator fault[J]. Nonlinear Dynamic,2015,81(1—2):1—15.
[7] YE D,PARK J. Adaptive robust actuator fault compensation for linear systems using a novel faults estimation mechanism[J]. International Journal of Robust & Nonlinear Control,2015,26(8):1597—1614.
[8] 王君,姚晓婉. NNCS混合容错控制方法[J].控制与决策,2018,33(2):316—329.
[9] SAMIR Z,HEMZA M. Actuator fault tolerant control using adaptive RBFNN fuzzy sliding mode controller for coaxial octorotor UAV[J]. ISA Transactions,2018,26(8):256—268.
[10] YANG P ,MA B. Fault-tolerant consensus of leader following multi-agent systems based on distributed fault estimation observer[J]. International Journal of Control Automation and Systems,2018,16(5):1—9.
[11] XIE C,YANG G. Decentralized adaptive fault-tolerant control for large-scale systems with external disturbances and actuator faults[J]. Automatica,2017,85(8):83—90.
[12] 張进,彭晨. 基于事件触发的网络化T-S模糊系统容错控制[J]. 信息与控制,2016,45(1):73—85.
[13] DU D,XU S. Actuator fault detection for discrete-time switched linear systems with output disturbance[J]. International Journal of Control,Automation and System,2017,15(6):2590—2598.
[14] WANG X ,XIANG C. Robust adaptive fault-tolerant control of a tandem coaxial ducted fan aircraft with actuator saturation[J]. Chinese Journal of Aeronautics,2018,16(2):365—378.
[15] 刘聪,钱坤. 基于LMI的一体化鲁棒主动容错控制器设计[J]. 控制与决策,2018,33(1):53—59.
[16] 彭晓易,武力兵. 一类带有执行器故障不确定线性系统的自适应H无穷控制[J]. 辽宁科技大学学报,2017,40(4):292—297.
[17] 邓伟璍,费敏锐. 带有执行器故障的网络控制系统的自适应容错H无穷控制[J]. 控制理论与应用,2010,27(2):269—272.
[18] GE X,HAN Q L. Distributed event-triggered H-infinity filtering over sensor networks with communication delays[J]. Information Science,2015,29(1):128—142.
[19] BURDAKOV O P,KANZOW C,SCHWARTZ A. Mathematical programs with cardinality constraints:reformulation by complementarity-type conditions and a regulation method[J]. SIAM Journal on Optmization,2016,26(1):397—425.
[20] TAO G,CHEN S H. An adaptive actuator failure compensation controller using output feedback[J]. IEEE Tr- ansactions on Automatic Control,2002,47(3):506—511.

