基于GA优化RBF神经网络的机器人轨迹规划

胡晓伟　安立雄　王宪伦

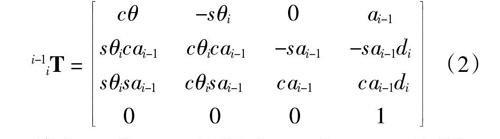
摘   要：针对机器人在不确定环境下末端执行器运动轨迹的准确性及平稳性问题，采用基于遗传算法（GA）优化径向基函数（RBF）神经网络的轨迹规划方法对Kinova Mico2机器人进行轨迹规划研究。介绍了机器人的相关参数及坐标系、建立了D-H矩阵和运动学模型。提取机器人实际抓取物品的直线轨迹并等分插补，用GA优化并实时在线更新RBF神经网络的权值，以更优的权值参数建立新的RBF网络。研究结果表明：相比优化前，基于GA优化RBF的规划轨迹逼近误差小且平滑稳定，仿真结果较为稳定，轨迹规划的可行性满足机器人实际抓取工作的需要。

关键词：遗传算法;机器人;RBF神经网络;轨迹规划

中图分类号：TP249                                             文献标识码：A

Robot Trajectory Planning Based on GA Optimized RBF Neural Network

HU Xiao-wei，AN Li-xiong，WANG Xian-lun

（College of Electromechanical Engineering，Qingdao University of Science and Technology，Qingdao，Shangdong 266042，China）

Abstract：Aiming at the accuracy and stability of the end effector's motion trajectory in uncertain environment，the trajectory planning method based on neural network of optimized radial basis function（RBF） with genetic algorithm（GA） is used to study the trajectory planning of Kinova Mico2 robot. The related parameters and coordinate system of the robot are introduced，and the D-H matrix and kinematics model are established. Extract the linear trajectory of the robot to actually grab the item and divide it equally，use GA to optimize and update the weight of the RBF neural network online，and establish a new RBF network with better weight parameters.The research results show that the planning trajectory approximation error based on GA optimization RBF is small and smooth and stable，and the simulation results are stable. The feasibility of trajectory planning can meet the needs of the actual robot grabing work.

Key words：genetic algorithm;robot;RBF neural network;trajectory planning

大多数机器人末端执行器安装有夹具以适应不同物体的抓取。机器人从抓取起始位到放置位的轨迹因控制系统采用轨迹插补算法，且因本体基座不稳、电机扭矩不足、惯性力大等不确定因素，不可避免使末端执行器存在运动不流畅或冲击力较大的问题，直接导致其无法准确到达抓取点位置。机器人运动过程大多存在逼近效果差、运动轨迹不连续、抓取精度低等问题，当机器人工作在不确定环境下时问题尤为突出。引入适当的运动轨迹规划算法势在必行。

径向基函数（Radial Basis Functions）广泛应用于全局或局部优化中，能快速收敛逼近任意非线性函数[1]。在解决相同精度问题时，RBF作为前馈型网络较BP网络具备节点配置更灵活、泛化能力更好等优点。但RBF网络的参数若选择不当则会导致训练迭代误差过大或数据不收敛。利用遗传算法GA其鲁棒性强、全局并行搜索能力高等特點优化RBF的权值参数以提高预测精度并避免局部极小值。为了更好保证机器人末端执行器按照期望的轨迹运动[2]，文献[3]提出了沿预定几何路径的时间最优的非线性动力学模型，将其应用于六轴工业机械手，借助加速度计等仪器跟踪了误差，进一步强调施加轨迹约束的重要性。文献[4]仅采用RBF神经网络对6DOF机器人轨迹进行误差研究及轨迹规划，因RBF算法本身缺陷未能准确预测不确定环境下机器人末端执行器的运动轨迹，更无法进一步补偿误差。文献[5]提出了一种基于标准正态分布的值函数的快速扩展随机树（RRT），用来规避RBF陷入局部极小点，保证了系统在机器人动力参数已知的情况下实现精准的轨迹规划。文献[6]基于GA遗传算法对模糊RBF网络的权值参数优化用来控制外骨骼灵敏度的放大比例。通过在线调整权值的方式更好地提升非线性曲线的拟合收敛速度，在机器人跟随人体运动轨迹时有较高的精度。

针对机器人末端执行器在线优化轨迹规划的研究较少，本研究以实验室已有加拿大Kinova公司生产的Mico2机械臂为实验对象，在上述文献基础上，提出了基于GA优化RBF神经网络规划机器人末端执行器运动轨迹的方法。RBF克服不确定环境下的机器人受到扰动产生的运动误差以逼近控制系统运动轨迹，GA则在线优化更新RBF的权值参数。基本思路是首先通过逆运动学解析并插补分割机器人末端执行器抓取目标的直线轨迹，并将各点转化为六轴关节角相应的弧度;接下来建立RBF网络，训练得到一组较优的离散解;最后通过GA对RBF优化训练权值，使用新网络优化得到最优离散解。使最终得到的最优规划路径能够满足实际的机械手抓取要求。

1   引入机器人运动学模型

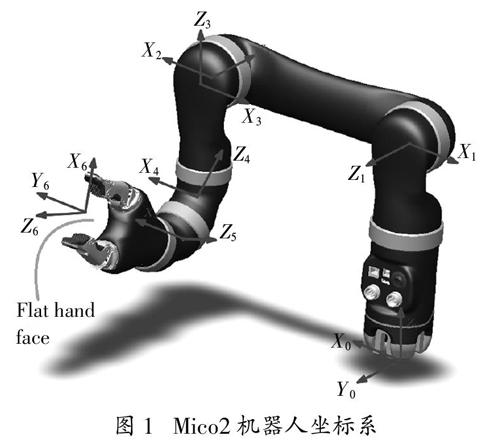
采用Mico2末端非正交六轴机械臂如图1所示，机器人自带夹具作为末端执行器。

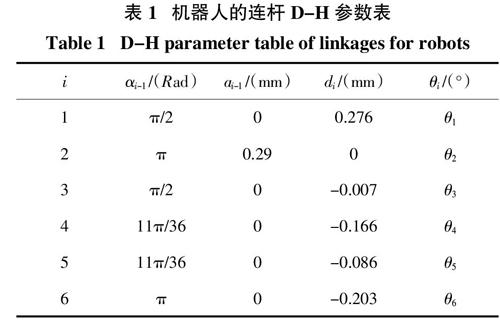
在规划机器人运动轨迹之前，需先求得机器人本体的各轴关节角与末端执行器工作空间笛卡尔坐标系位姿的关系，即建立改进的D-H矩阵如表1所示，以求解正逆运动学得到位姿矩阵和各关节角 ，通过各轴坐标的转换关系得到末端执行器的实际工作位置和姿态。求得正逆運动学转换关系后进行手眼标定，确定好工业相机与机器人夹具的坐标转换关系，以“手在眼外”的方式安装相机。

图1   Mico2机器人坐标系

表1   机器人的连杆D-H参数表

Table 1   D-H parameter table of linkages for robots

工业相机拍摄抓取场景重建点云模型，用以确定待抓目标物的抓取点坐标。描述末端执行器相对于基座的位置关系BTT：

BTT = R   T0    1    （1）

其中矩阵R表示机械手末端执行器姿态，T表示位置三维坐标。

1.1 运动学推导

通过D-H矩阵参数采用后置坐标系法建立各连杆坐标系的变换关系：

i-1iT =    cθ          -sθi          0            ai-1 sθicai-1     cθicai-1     -sai-1     -sai-1disθisai-1     cθisai-1      cai-1        cai-1di    0             0            0             1（2）

其中cθi为cosθi的简写，sai-1为sin ai-1的简写等。

将各连杆参数代入式（2）得到各连杆齐次变换矩阵，按序相乘得

06T = 01T 12T 23T 34T 45T 56T                     （3）

因Mico2机器人腕部三个关节非正交，不满足Pieper准则，因此需根据牛顿数值迭代法对其进行逆运动学求解。

通过式（3）可实现在机器人工作范围内给定六轴关节角弧度值θi计算得出末端执行器唯一位姿解，即完成运动学正解。反之已知末端执行器位姿4 × 4位姿矩阵可通过数值迭代求解六轴关节的各转角弧度值，即完成运动学反解。进一步通过构建雅可比矩阵求得各连杆铰接处关节速度。

1.2   插补算法

为缩短抓取时间，采用起始位至抓取位的空间点对点三维直线路径。已知相对于机器人基座坐标系的空间始末两点Ps（xs，ys，zs）、Pe（xe，ye，ze），根据均速v及间隔时间 即可得到插补总数N：

N=（■/vti） + 1

（4）

各插补点的坐标值为：

xi+1 = xi + i（xs - xe）/Nyi+1 = yi + i（ys - ye）/Nzi+1 = zi + i（zs - ze）/N          （5）

2   RBF神经网络参数特性

2.1   RBF逼近理念

RBF网络具备不同于BP网络所具有的局部逼近特性[7-9]。每当非线性轨迹矩阵输入时，由于高斯分布公式在RBF中用作神经元激活函数，因此当且仅当与输入样本向量所接近的神经元（隐含层非线性映射）及权值才运作。相对于BP的全局优化，RBF则能以更快的速度和更小的计算量逼近输出值，更好地克服了隐含层过拟合现象。RBF函数逼近模型为：

yo = ■gio？准（‖x-ui‖2），（o = 1，…，p）    （6）

一般地，隐含层激活函数一般为：

？准（‖x-ui‖）=exp（-‖x-ui‖2/σ2）     （7）

其中‖x-ui‖输入与基函数差向量的2范数; yo为网络输出量;ui为第 个节点的中心矢量;p为隐含层神经元数;？准为高斯核函数;g为网络权值矩阵;σ为高斯常数。显然，每个输入值在不同的隐含层节点都会输出一个基于高斯核函数的值，且最终输出值为最接近中心矢量的值。

2.2   RBF确定权值参数

RBF属前向型网络，包含输入层、隐含层及输出层三层[10-12]。各隐含层神经元的输出按照各自g加权求和得到线性输出层。设定近乎小的正实数δ、轨迹插补矩阵x和最优轨迹插补矩阵X*，存在最优权值g*满足：

max‖X* - x‖≤δ       （8）

X* = （g*）T？准（‖x-ui‖2）      （9）

因此当且仅当μ = X* - x无限收敛与零时，可以准确并快速逼近输出值。

3   GA优化RBF网络的轨迹规划

3.1   GA优化理念

针对权值g的训练方式大部分采用LMS、PSO、GA等方式，遗传算法GA具有更好的并行全局搜索能力，在训练过程中自适应并控制训练过程。

为了解决实际问题，将GA算法以合适的形式合理构造[13]，在算法规定的迭代过程中，以N作为种群规模，每次迭代生成参数值：

αn = gT    n = 1，2，3，…，N      （10）

设定各关节角误差因子及迭代最小值目标函数：

ηi = θi - θ*i    i = 1，2，3，4，5，6      （11）

Ln = ■ηi    n = 1，2，3，…，N      （12）

根据式（13）构造一个用来评价染色体优劣程度的函数：

Fn = 1/Ln    n = 1，2，3，…，N      （13）

易知Fn越大，染色体越优[14]。对于交叉算子，从父代群体任意选择两个体x1、x2，进行单次迭代交叉组合生成新的后代：

x′1 = λx2 + （1 - λ）x1x′2 = λx1 + （1 - λ）x2     （14）

其中λ為随机产生的实数。为了确保使搜索范围保持在较大的空间进行，因而需对染色体进行变异操作，在二进制编码中，染色体随机由0和1互转。这里采用动态设置方法，设定fMax是种群最大适应度，fAvg是种群均值适应度，交叉概率Pc和变异概率Pm随适应度改变。则交叉起始概率Pc1 Pm1与交叉变异概率Pc2 Pm2的关系如下：

Pc = Pc1 - （Pc1 - Pc2）■，f ≥ fAvgPc1， f ≥ fAvg     （15）

Pm = Pm1 - （Pm1 - Pm2）■，f ≥ fAvgPm1， f ≥ fAvg   （16）

3.2   算法实现

GA优化RBF模型的学习过程如图2所示。构造GA_BRF网络轨迹规划控制系统如图3所示。

图2   GA优化RBF模型的学习过程

图3   GA_BRF网络轨迹规划控制系统

实现步骤如下：

（1）在机器人的笛卡尔坐标系工作区间内，相机拍摄重建抓取场景并提取抓取点三维XYZ坐标。

（2）控制系统通过公式（2）（3）将位置信息转化成末端执行器基于基座的齐次变换位姿矩阵BTT。

（3）在Matlab中通过公式（5）插补整条轨迹并按逆运动学反解出六个关节所需转动的角度θi。

（4）在运动过程中，由RBF实时接收末端执行器反馈给控制系统的实际关节角矩阵x，GA实时训练RBF隐含层与输出层的权值g*.

（5）经训练后的RBF优化处理关节角矩阵x，再将新的关节角矩阵X*发送至控制系统进而补偿由不确定因素导致的运动误差.

4   轨迹优化仿真实验

本研究验证GA_BRF网络进行轨迹规划的可行性，建立如图4所示的Mico2机械臂数学模型。

图4   Mico2机械臂数学模型

以Mico2机械臂末端执行器的轨迹运动为跟踪对象，确定好起始坐标点（220，-100，0）抓取坐标点（300，-200，100），模拟一段自起始位开始的空间运动的抓取直线轨迹如图5所示。转换得到位姿矩阵为

BTT始 = 0.26    0.54    0.06    2200.15    0.21    0.19   -1000.33    0.01    0.75      0  0          0         0        1

BTT末 = 0.33    0.21    0.13    3000.04    0.12    0.05   -2000.17    0.06    0.11    100  0          0         0        1

图5   抓取直线轨迹

设定始末15秒内每0.2秒插补一点，共计76个点。通过逆运动学解析每个关节角所转的角度并绘制变化轨迹如图6所示。运动过程中，GA_RBF网格实时训练优化各关节角数据。最终将最优关节角规划值导入到控制系统，以供控制系统补偿在不确定环境下造成的轨迹误差。

位置

时间/s

图6   各关节角运动轨迹

以第1轴关节角始末变化为例，生成由未优化原始轨迹、RBF预测轨迹及GA_RBF训练优化预测轨迹对比轨迹曲线图。如图7所示，显然GA优化预测输出的关节运动轨迹曲线整体与实际输出的轨迹大致接近，并且曲线光滑无局部冲击点。

论文关切角位移变化数据

时间/s

图7   原始、RBF、GA_RBF曲线对比

5  结  论

虽然RBF与GA_RBF都可以对在不确定环境下的末端执行器进行轨迹预测。但在保证位置精度、运动平稳前提下，GA_RBF网络能更快将轨迹误差收敛在一个较小领域内且避免局部最小值，从而使优化轨迹与控制系统轨迹误差尽可能缩小，也使机器人在更短的时间内达到稳定状态。验证了基于GA优化RBF神经网络的机器人轨迹规划的可行性。本研究对于工业机器人码垛作业或焊接作业具有极高的实际应用价值。

参考文献

[1]    肖凡，李光，周鑫林.多连杆机械臂GA-RBF神经网络轨迹跟踪控制[J]. 机械科学与技术，2018，37（05）：669—674.

[2]    辛大欣，刘少贞.基于RBF神经网络的机器人平滑圆弧轨迹规划[J]. 计算机与数字工程，2016，44（03）：409—413+424.

[3]  REYNOSO-MORA P，CHEN W，TOMIZUKA M. A convex relaxation for the time-optimal trajectory planning of robotic manipulators along predetermined geometric paths[J].Optimal Control Applications and Methods，2016，37（6）：1263—1281.

[4]    刘益标，陈均. 基于径向基函数神经网络控制的机械臂轨迹误差研究[J]. 机床与液压，2018，46（15）：105—108.

[5]    JINWOOK H，DANIEL L. Efficient sampling with q-learning to guide rapidly-exploring random trees[J]. IEEE Robotics and Automation Letters，2018，3（4）：3868—3875.

[6]    龙亿，杜志江，王伟东. GA优化的RBF神经网络外骨骼灵敏度放大控制[J]. 哈尔滨工业大学学报，2015，47（07）：26—30.

[7]   KIM Dong-hyung，CHOI Youn-sung，KIM H. Collision-free trajectory planning of a dual-arm robot using a B-spline curve[J]. Journal of Institute of Control，Robotics and Systems，2017，23（3）：203—212.

[8]    许刚.基于GA-RBF的煤矿机器人井下混合气体检测系統的研究[J].计算技术与自动化，2018，37（03）：66—68.

[9]   ALAM T，BOBADILLA L，SHELL DYLAN A. Space-efficient filters for mobile robot localization from discrete limit cycles[J]. IEEE Robotics and Automation Letters，2018，3（1）：257—264.

[10]  强宁，高洁，康凤举.基于PSO和三次样条插值的多机器人全局路径规划[J].系统仿真学报，2017，29（07）：1397—1404.

[11] VEJDANNIK M， SADR A， Automatic microstructural characterization and classification using dual tree complex wavelet-based features and bees algorithm[J]. Neural Computing and Applications，2017，28（7）：1877—1889.