推理能力培养三部曲——以“多边形内角和”教学为例

□夏小林 朱新强

推理能力的培养是数学课程与课堂教学的重要目标。在小学数学教学中应该如何培养学生的推理能力呢？笔者以“多边形内角和”教学为例，谈谈自己的体会。

一、把握本质，让知识成为思维的载体

对比人教版和北师大版教材中有关“三角形内角和”的教学内容，我们发现，这两个版本的教材中都专门安排了“发现”活动：先引导学生通过量一量、算一算，发现三角形内角和在180°左右，然后借助撕拼活动进行验证，发现三角形三个内角可以撕拼成平角，再根据平角含义得出三角形内角和是180°这个结论。不同之处在于：人教版教材直接明确“画几个不同类型的三角形”，分类研究的数学思想表达得更充分；北师大版教材则以表格的形式呈现，引导学生关注“三角形的形状”，渗透分类思想。另外，北师大版教材还告知学生“测量有误差”。

传统的教学往往以得出知识结论为主要目标，不太重视思想方法的渗透，特别容易忽视知识背后“推理能力”的培养。在本课教学中，我们以“推理”为主线，先通过对一个锐角三角形内角和的测量求和，形成猜想：是不是所有的三角形内角和都是180°？在此基础上引导学生分类研究，以组为单位，分别测量计算锐角三角形、直角三角形、钝角三角形的内角和，然后通过不完全归纳法，得出每一类三角形的内角和。最终在“类”的层面上实现完全归纳，从而推理出所有三角形内角和是180°的结论。另外，借助撕拼法让学生确信所测量的三角形内角和就是180°，同时体验到证明方法的多样性。本课的教学设计将多边形内角和教学整合为一课时，以三角形内角和为基础，并借助三角形内角和是180°，推理出四边形、五边形的内角和，渗透探究多边形内角和的一般方法和模型。

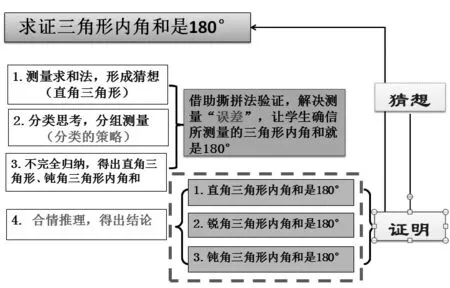
本节课的教学设计框架如下：

二、形成猜想，让学生站在推理的起点

牛顿曾说：“没有大胆的猜想，就没有伟大的发现！”学习数学的过程中，引导和鼓励学生提出猜想十分重要。合情推理的实质是“发现—猜想—验证”的过程，而培养合情推理能力应以观察为基础，以猜想为桥梁，以想象为动力。教师要为学生营造一个可供猜想的情境，让学生借助有利于引发猜想的素材，有机可“猜”。

【教学片段1】

（1）提出问题，形成猜想。

师（出示三角形）：你有什么办法可以知道它的内角和吗？生：量一量它的三个内角的度数，然后加起来。（生操作，师指导）

师：通过测量，我们知道了这个三角形的内角和是180°。现在，关于三角形的内角和，你有没有一个大胆的猜想呢？

（2）讨论交流，思考策略。

师：我们刚刚只知道这个三角形的内角和是180°，是不是就可以说所有三角形的内角和都是180°呢？

在前测中，我们发现班中的大部分学生已经知道三角形内角和是180°这个结论，但并不清楚这一数学事实的来由。所以教师在这个环节请学生测量锐角三角形内角并求和，目的不是得出三角形的内角和是180°，而是形成猜想：是不是所有三角形的内角和都是180°？从研究问题和解决问题的角度，教师提供了按角分类的研究思路，渗透了“分类的策略”，为合情推理提供了充分的依据。撕拼法是教师用课件演示的，这主要是因为在试教中我们发现学生自己很难想到，而撕拼法的价值在于发现任意三角形的内角都可以拼成一个平角，而平角为180°，从而推导出三角形内角和为180°。借助撕拼法验证，让学生确信测量的三角形内角和就是180°。

三、经历过程，让学生体悟推理

（一）从“形成猜想”到“合情推理”三角形内角和是180°

著名数学教育家波利亚认为：“合情推理是数学发现与创造的源泉。”合情推理是数学发现过程和数学体系建构过程中的一种重要思维形式。合情推理可分为归纳推理和类比推理两类，简言之，归纳推理是由部分到整体、由个别到一般的推理；类比推理是由特殊到特殊的推理。

【教学片段2】

师：请第一大组任意画一个直角三角形，第二大组任意画一个锐角三角形，第三、第四大组任意画一个钝角三角形，然后量一量，算一算，看看它们的内角和是不是180°。

（生操作，师指导……之后反馈三种类型三角形的内角和）

师：通过测量法、折纸法，我们知道了直角三角形、锐角三角形、钝角三角形的内角和都是180°，那么可不可以说所有三角形的内角和是180°了呢？

生：可以。

本课教学中，在反馈每一类三角形内角和时，采用的是不完全归纳法。以直角三角形为例，即使组内每一个学生画的直角三角形都不相同，我们也无法完全列举其所包含的全部情况，但是，当每一类三角形的内角和的结论都得出后（如下图），在“类”的层面上就实现了完全归纳。

（二）从“自主探究”到“演绎推理”四边形、五边形内角和

如果说三角形内角和180°是通过提出猜想、合情推理得到的，那么四边形、五边形内角和结论的得出，是经历完整的演绎推理的结果。

【教学片段3】

师：同学们，现在我们研究四边形、五边形的内角和。如果不量、不折、不拼，你们能不能应用刚刚学到的三角形内角和的知识，来推理出四边形和五边形的内角和呢？

（生操作，师指导）

师：你们想到办法了吗？生：在四边形中画一条线，将它变成两个三角形，每个三角形的内角和是180°，那么四边形的内角和就是180°×2=360°。（如右图）

四边形的内角和是几度呢？学生须静下心来观察思考：四边形如何与三角形发生联系，进而再与三角形内角和的知识进行联系？渐渐地，“分”的意识在学生脑海中萌芽，通过尝试连对角线（添辅助线），学生惊喜地发现任意一个四边形都可以分成两个三角形，四边形的内角和，也就是两个三角形内角的总和，即180°×2=360°。通过演绎推理可得，四边形的内角和是360°。在此基础上，教师又进一步引导学生经历完整的推理过程，清晰而严谨地表述推理过程。

推理四边形内角和360°框架

任意一个四边形都可以分成两个三角形（大前提）

任意一个三角形的内角和都是180° （小前提）

所以任意一个四边形的内角和都是360°（结论）

三段论是演绎推理的一般模式，它包括：（1）大前提——已知的一般原理；（2）小前提——所研究的特殊情况；（3）结论——根据一般原理，对特殊情况作出的判断。探究发现的路，就是创新之路。把未知的知识转化成已知的知识解决问题，既是策略，又是重要的数学方法，是演绎推理本质的体现，即从已有知识得出新知识，特别是得到不可能通过感觉经验掌握的新知识。

（三）从“知道结论”到“模型思想”，感悟多边形内角和计算的一般方法

【教学片段4】

师：同学们都有自己的收获。现在，请你们观察一下这几个算式，发现什么规律吗？

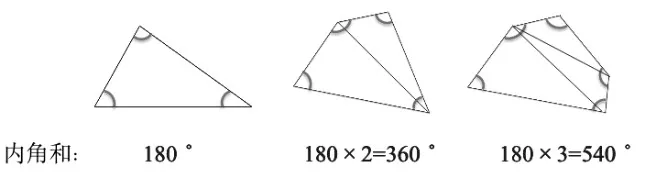
生：我发现，每增加一条边，内角和就多180°。

生：我发现，四边形可以分成2个三角形，五边形可以分成3个三角形。

师：那么，除了这几个图形外，你知道还有哪些多边形吗？

师：那你能不能也用我们学过的知识，来推理出这些多边形的内角和呢？这个问题就留给大家课后再去研究了。

有了四边形、五边形内角和推理的基础，六边形以及更多边形内角和的推理，在方法运用上已经水到渠成了。得出“多边形内角和”的计算模型，是本堂课“锦上添花”的一笔！

纵观整节课的学习路径：三角形内角和教学，以实例测量形成猜想，合情推理；以“三角形内角和是180°”，运用演绎推理证明四边形、五边形内角和，合情推理、演绎推理两种推理方式相得益彰。合情推理的结论需要演绎推理的验证，演绎推理可以验证合情推理的正确性，合情推理可以为演绎推理提供方向和思路。一句话：合情推理使学生“知其然”，演绎推理使学生“知其所以然”。