运中有智慧 算中有妙法——小学生运算能力培养的思考

□钱利平

《义务教育数学课程标准(2011年版)》中指出，“运算能力主要是指能够根据法则和运算律正确地进行运算的能力。培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题”。这两句话实际上刻画了运算能力的三个主要表现特征:正确运算、理解算理、方法合理。那么，新课标提出8 年了，对运算能力而言，现状又是怎样的呢？

为了对学生情况有比较准确的了解，我们对某校83名学生进行了一个小样本调查。

调查材料：请你用自己喜欢的方法算：36×0.25（其中一道前测题）。结果如图1所示。

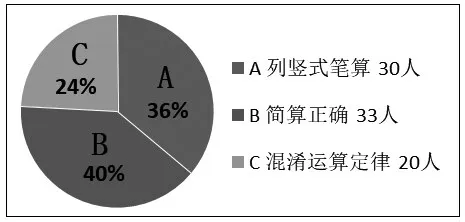
从前测情况看出：学生的笔算意识相当强，但对运算意义的理解不深刻。正是基于这样的教学现状，我们思考：运算能力作为数学学科独有的关键能力，能否将它拆分为“运”的能力与“算”的能力？“运”是意识、思想、策略，是一种思维活动；“算”是技能、实践、演练，是一种操作活动。要培养学生的运算能力，不仅要培养学生“算”的能力，更要培养学生“运”的能力。因此，教学中要体现先“运”后“算”，边“运”边“算”，“算”后再“运”这样的计算教学特色，让“运”贯穿于“算”的全过程。一个学生如果头脑里“运”清楚，“运”明白了，“算”就是水到渠成的一件事。

一、运意识之道，求算法之简

“意识”是指人的头脑对客观物质世界的反映，也是感觉、思维等各种心理过程的总和。遇到36×0.25，为什么会有36%的学生选择列竖式笔算？说明学生没有求简意识。那么教师该如何运意识之道呢？第一，学生在运算前要有简算的意识，想一想“能简算吗”；第二，学生在运算时要有质疑辨析的意识，思考“我这样算有根据吗”；第三，学生在运算后要有反思检查的意识，自查“算得对吗？算得巧吗”。

（一）能简算吗？——唤醒“简算意识”

在计算教学中，教师往往重视让学生低头算，却忽视了让学生抬头想。因此，在36×0.25 的教学中，笔者提问：“不列竖式计算，你还有别的方法吗？”通过呈现学生的四种不同算法，引发学生的思维碰撞（如图2）。

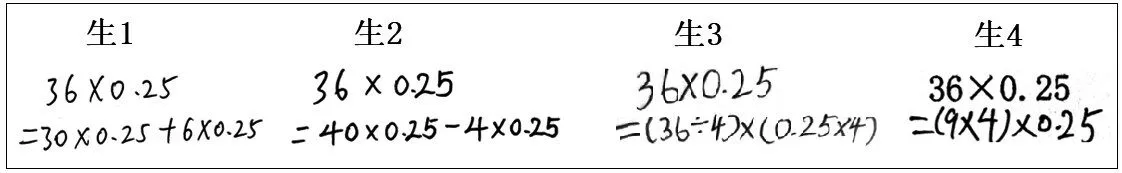
图2

这四种算法的呈现是有视觉冲击的，它明确地告诉学生，一道计算题，可以有不同的简便算法，每种算法只要有根据，就是合理的。因此学生在计算时，潜意识里要有高效运算的“简算意识”。

（二）有根据吗？——发展“依据意识”

合理的算法，需要知道合的是什么理，根据什么样的运算律，运算律又是根据什么样的运算义。对于图2中的四种算法，笔者引发学生思考：“这些算法都有根据吗？”通过对比辨析，学生既感受到算法的多样化，又对算法合理性的本质再次内化，“依据意识”深入人心。

我们来看，生1和生2运用了乘法分配律，生3运用了积的变化规律，生4运用了乘法结合律。学生从“不同的运算定律”中感悟到“运算意义的相同”，即都是36 个0.25 相加，这是算法背后的“依据”，也是算法的“根”。一旦算理扎根，学生在运算时，只需要对与之相关的运算顺序、运算法则和运算定律进行灵活运用，就能做到有律可依，达到计算过程的“简化”。

（三）算得对吗？算得巧吗？——深化“反思意识”

学生在交流、辨析和比较中，会找到适合自己的最优算法。如在对36×0.25的几种算法的反馈过程中，通过对比笔算方法和学生常见的错误：（4×9）×0.25=9×0.25+4×0.25，引发学生自查：“表示的是36个0.25吗？你喜欢哪种算法？”同时，在对“算得对吗”“算得巧吗”这两个问题的反思觉察中，通过对最优算法的欣赏评价，进一步深化学生“反思检查”的意识。

因此，教师要让学生在计算时，运意识之道。学生在“能简算吗”“有根据吗”“算得对吗？算得巧吗”这样一连串问题的自我设问中，不断地进行自我觉察，自我调整，从而求得算法之简。

二、运规则之道，正算法之理

计算规则一般有两类：一类是法则，根据法则确定运算顺序；一类是定律，根据定律可以打破既定的运算顺序。在计算中，学生往往会出现两类情况：第一类是该依法则计算时却按定律算，表现为“不能简算的乱简算”；第二类是该依定律计算时却按法则算，表现为“能简算的不简算”，这反映出学生对“法则”和“定律”的本质理解不清晰、不到位的问题。那么，如何在教学中运规则之道，正算法之理呢？

（一）认清法则，让算法有根可寻

法则是人们在计算中自然形成的一种计算规则，是小学数学规则的主要表现形式之一，它广泛地存在于数与代数、图形与几何、统计与概率等内容之中。

在教学中，教师应严格要求学生按照相应的定理、定义和法则理解题目，让学生逐渐养成遵守法则的习惯。与此同时，还需要让学生认识到不遵守法则的后果。例如，在加减混合的综合算式计算教学过程中，为了让学生认识到“从左往右”的计算顺序，教师可出示这样的题目：10-7.5+2.5＝？，学生可能会给出5 和0 两种答案，此时教师便可以告诉学生正确答案，让学生清楚地认识到加减混合算式的运算法则，从而逐渐培养学生的规则意识。

（二）厘清定律，让算法有律可依

运算定律是一种模型化知识，是对数的运算过程中基本规律的归纳与总结。然而，在教学实践中我们发现，学生混淆运算定律的情况特别多。例如1.25×2.5×12 一题，混淆运算律的情况主要有以下两种（如图3）。

图3

学生只关注到1.25×8 以及2.5×4 可以凑整，而对算式的结构特征认识模糊。对数据的片面关注导致学生对乘法结合律与乘法分配律混淆不清。那么如何帮助学生厘清定律，对运算律有清晰的认识呢？教师可以结合具体情境展开教学（如图4）。

图4

把2.5变成长方形木板的长，1.25变成长方形木板的宽。一方面，学生更加倾向把1.25×2.5这一块木板的面积当成一个“整体”，有效规避了错误；另一方面，从乘法分配律的结构特征入手，强化学生的结构意识，使学生对运算定律的结构印象深刻。

由此可见，运规则之道，帮助学生厘清法则和定律，有助于培养学生合理选择算法的能力，发展学生思维的灵活性。

三、运策略之道，释算法之义

运算策略水平是鉴别学生运算能力高低的一个敏感因素。运策略之道，一方面可以与现实背景相结合，赋予计算在实际生活中的价值；另一方面可以借助“数形结合”，通过几何直观，使抽象的计算教学变得具体形象。

策略1：与现实背景相结合，以现实模型释算法之义

小学数学中的计算题往往取自生活原型。给运算赋予现实背景，可以让纯粹的计算变得鲜活。比如，在探究《乘法分配律》一课中，笔者在课堂上出示如下情境。

（1）学校购买春装校服,每件上衣50元，每条裤子45 元，买这样的30 套衣服一共要多少元？（只列式不计算）

（2）在一个长方形花圃里栽郁金香和菊花（如下图），这个花圃占地多少平方米？（只列式不计算）

通过列式，学生出现了两种思路的算式表达——“先求和，再相乘，即（a+b）×c”或“先分别乘，再相加，即a×c+b×c”。从现实背景入手，通过对数学模型的解构，让运算意义或算理的解释与现实问题的解决融合起来，让学生理解算法的“要义”。

策略2：与平面图形相结合，以数形结合释算法之义

华罗庚老师说过，“数形结合百般好，隔离分家万事休”。几何直观是数学课程标准提出的十个核心概念之一，主要是指利用图形描述和分析问题，帮助学生直观地理解数学，研究问题。

例如在教学1.25×2.5×12 时，教师可以借助长方形，帮助学生建立正确的表象。如何引导学生正确计算呢？学生想到“1 块木板的面积×12”：1.25×2.5×12，一个一个看，显然算起来比较麻烦。这时教师提出可以结合图，使计算更简便。引导学生算

大长方形的长×宽：（2.5×4）×（1.25×3）（如图5）；也可以算一行的面积×3：（2.5×4×1.25）×3（如图6）。两种方法都利用了2.5×4 可以凑整的数据特征，达到简算的目的。而且这两种算法沟通了“运算意义”和“运算定律”之间的关系，帮助学生理解算理。

图5

图6

那么可不可以算一列的面积×4 呢？（1.25×3×2.5）×4，显然这样计算是比较麻烦的。这道题目很有意思，在图形意义的指导下，利用数据的特征，引导学生先思维后计算，从而培养学生良好的计算习惯。由此可见，运策略之道，就是让每一种算法，既能找到生活原型，又能找到图形对应，使每种算法都有理有据。

运中有智慧，算中有妙法。如果把运算中的“运”和“算”放在二维体系中，它们应该是有一定正比关系的，“运”的能力越弱，“算”的方法可能只局限在“对”上；“运”的能力一般，“算”的方法只能求好；“运”的能力越强，则“算”的方法就越巧。在当下计算教学格局重“算”的背景下，我们力图重“运”，培养学生运中求道，以道驭法，这样“道法自然”的计算课，正是我们所追求的！