用多元函数求值域方法解线性规划问题

贵州省毕节市梁才学校 (551700) 罗导江

例2 (2019年北京卷理5)若x，y满足|x|≤1-y，且y≥-1，则3x+y的最大值为( ).

A.-7B.1C.5D.7

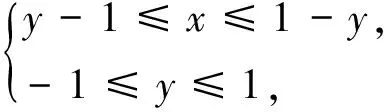
由于z(x)为增函数z(x)max=z(1-y)=3-2y(-1≤y≤1)，又令z(x)max=z(1-y)=T(y)=3-2y(-1≤y≤1)，则T(y)max=t(-1)=5，即3x+y的最大值是5，选C．

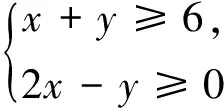
A.①③B.①②C.②③D.③④

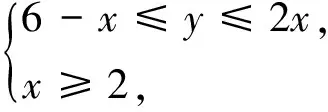
上述用多元函数求值域(最值)解线性规划的方法还可推广到求约束条件是方程﹑不等式混合组的多元函数值域(最值)上.

例5 已知x,y,z∈[0,1]，且x+x+z=2，求2x+3y+4z的最大值.

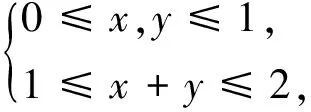
练习题已知x,y,z∈[0,1]，且x+y+z=2，求x+y2+z3的最小值.