让理性的思维在课堂上轻舞飞扬
——以一节以思维发展为主线的探究课为例
广东省广州开发区中学 (510730) 胡晓丽广东省广州开发区外国语学校 (510700) 蔡军喜
对学生进行“素质教育”、让学生“减负增效”、培养学生的“核心素养”……,随着新课改的不断深入,面对一个又一个新思想、新理论的提出,一线数学教师该教什么?如何教?南京大学郑毓信教授在《中国数学教育的“问题特色”》一文中为我们指明了方向:“数学教育的主要任务是促进学生思维的发展,特别是,即应通过教师的教学帮助学生逐步学会更清晰、更深入、更全面、更合理地进行思考,并能由‘理性思维’逐步走向‘理性精神’,即是真正成为一个高度自觉的理性人,应高度重视数学教学中的‘问题引领’与‘问题驱动’,这并可被看成更好地继承与发展‘中国数学教学传统’的一个很好的切入点 ”
1.问题提出
在复习完直线的方程、直线的垂直和对称后,给出如下问题让学生尝试练习:
已知点A(-2,1)、B(1,2),试在x轴上找一点P,使△PAB的周长最小.
此题背景平常,但其中蕴含的解题思想却极其深刻,仔细揣摩,极富有广泛的拓展空间.
2.问题解决
在教学中,我选择以学生的主动探索安排教学活动,首先不急于把解法抛给学生,而是引导学生分析问题的特性:该问题中两个点A,B确定,而第三点P在x轴上运动,结果即求|PA|+|PB|的最小值,是一个最值问题,那么我们该如何思索呢?

(一阵善意的轻笑声……)
师:我先来谈谈我的看法,首先“生1”同学的化归方法还是很好的,可谓处理最值问题的一个“通法”,代表了大多数同学的思维,但对本题来说,好像易想但不易用,那我们能不能变换角度,找一找有没有别的解法?(既肯定“生1”的想法,更鼓励大家继续努力)
(教室里一阵寂静……几分钟后)
生2:看到P为一动点,A、B为两定点,且|PA|+|PB|为两距离之和,我联想到了椭圆定义|PA|+|PB|=2a,进一步思索,我觉得P点的选择应是以A,B为焦点的动椭圆与x轴相切时取得最小值,但由于椭圆的方程为非标准位置,所以我也没能求出……
(台下一片赞叹声,我知道,他们一方面是同意他的观点,另一方面更是佩服他的勇气)
师:这位同学说得很对,我也同意他的观点,显然,若A,B两点移到x轴上,P为另一直线上的动点,借助“生2”同学的思考,应是较易求出的.生2的想法可谓独特,足见他的思维活跃,视野开阔,联想丰富,这是创造性人才应必备的素质.
(看到两位同学的踊跃发言,大家一脸跃跃欲试的表情……)
显然,两次不成功的体验和思维暴露,不仅没有挫败大家的积极性,反而激发了更大的共鸣.
生3:(兴奋的)我想到一种方法,要在x轴上找一点P使|PA|+|PB|最小,可作B点(或A点)关于x轴的对称点B′,连AB′,则AB′与x轴的交点即为所求P点,且最小距离为AB′=|PA|+|PB|.
师:你是怎么想到的呢?
生3:我联想到物理中的平面镜成像和光线以最短路径传输的原理和本题的模型相似.
(真是奇思妙想啊!一道题目让学生参与分析,不仅想到了椭圆的定义,还想到了物理中的光学性质,这是笔者始料不及的,学生的智慧真是无穷无尽.)
师:(点头微笑,充满信任,激励的表情)那么你能简要证明一下此时的值为何最小吗?
生3:能证明.
于是我请“生3”在讲台上作了一次精彩的“自我展示”
(一片惊叹声,更是一片议论声……)
师:感谢大家的积极思考,追溯历史,本题其实就是著名的“将军饮马问题”,历史上已经有很多研究结论和方法.但今天我们用独立思考方式,实践了一次前人的探索足迹,变结论的“冰冷美丽为火热的思考”.正所谓“探索诚可贵,体验价更高”!
3.问题拓展
到此,原始问题已经得到了圆满的解决,借助兴趣的提升,适时引导学生思维发展的高潮.
3.1 从特殊到一般
师:在上面的问题中,若我们将P点的位置从x轴上移到更一般的平面上任意一点,那么|PA|+|PB|有最小值吗?△PAB的周长有最小值吗?
生4:△PAB的周长无最小值,|PA|+|PB|有最小值,可分两种情况说明:
(1)若P点与AB不共线,则P,A,B三点构成三角形,易知|PA|+|PB|>|AB|;
(2)若P点在AB上时易知|PA|+|PB|≥|AB|,当且仅当P在A、B之间或与A、B两点重合时取得最小.
3.2 从静止到运动
师:(继续引导探索)若我们保持P点继续在x轴上运动,让静止的A点也在一条
直线l:y=2x+5上运动,那么|PA|+|PB|有最小值吗?△PAB的周长有最小值吗?

图1
生5:都有最小值,借助于原始问题,我们可将B点分别作直线l,x轴对称点E、F,如图1,设交l与x轴于点M、N,连接EF,设交l与x轴于点R、S,则|PA|+|PB|的最小值为|BN|+|BM|,△PAB的周长的最小值为|EF|,M、N;R、S分别为所求的A、P两点.
3.3 从几何到代数
师:透过以上问题的解决,我们再回头看看原始问题的函数解法,能否从中感受几何与代数的联系呢?
生6:原始问题中的目标函数的最值可借助点的对称,几何求解.
师:能否将原始问题的模型一般化并加以归纳深化呢?
(鼓励学生进行思考,允许他们展开讨论,并鼓励大家积极发表各自的看法)
生7:通过我们几个的研究,得到以下结论:
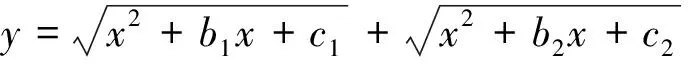
3.4 从平面到空间

图2
(1)若x轴伸展为平面,如图2,已知平面α同侧两点A、B,P在α上运动,|PA|+|PB|有最小值吗?△PAB的周长有最小值吗?若P在空间上运动呢?
(2)若x轴伸展为平面α,问题3.2中的l直线也伸展为平面β:如图3,已知二面角α-l-β的大小为θ,点B为夹在二面角内的空间一点,点A在α面内运动,P在β面内运动,那么|PA|+|PB|能否最小?△PAB的周长能否最小?
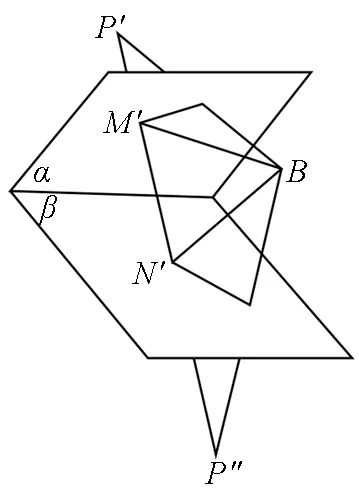
图3
3.5 从理论到实践
师:随着问题的条件、结论的不断发散,我们不仅解决了一类问题,也收获了几个重要模型,能否将模型付诸应用呢?(我尝试让学生对模型进行实际问题的编拟与应用,也收到了可喜的效果,很快,便有了小组编拟与应用问题)
问题1在一条河(近似笔直)的同侧有两个村庄,张庄和李庄,两村计划于河上共建一水电站,发电供两村使用,请建立数学模型,设计水电站的位置,使送电到两村使用的电线用料最省?



四、教学启示
问题不是新的,但过程却不是旧的,几经思维“冲浪”,看似平常的问题,依然有它强大的生命力.一堂课结束了,相信学生探究数学的工作仍在继续.本节课引例本是常规问题,但一改过去老师讲解、学生接受的教学模式,“行散而神不散”,既落实了垂直和对称知识,又把生成点放在解法的自主探索和思维方向的发散上:一是它激发了学生探究数学的兴趣和热情;二是本节课引导学生思维发散的方法和方式可迁移到其他问题的探索过程中,其潜在价值不容忽视;三是学生创造性思维的火花不断碰撞和相互启发,促进了每位学生思维的发展,使学生看问题的角度不断扩大,解决问题、提出问题、分析问题的能力不断拓升.
“教的最终目的是为了不教”,“授人以鱼,不如授人以渔”,教师工作的真正意义,不是单纯的传授知识,而应以数学知识为载体,以数学思想和方法为核心,以提高学生能力和素养为目的.弗赖登塔尔认为:“数学知识不是教出来的,而是研究出来的.”所以,我们必须让学生知道数学学习的本质是什么;我们必须注意于数学家所用的工作方式,并围绕它,而不是围绕着数学家工作的结果来组织教学,知识也许会“老”,但思考问题的方法却永远“年轻”.

