“数形结合”思想在高中数学不等式求解中的应用

蔺兴旺

摘要：在高中数学学习中，数形结合思想对于数学题的解题是非常有帮助的，学生学不好数学或者觉得数学难，在一定程度上有可能是因为在解题过程中对于数形结合思想的应用不够灵活变通。而不等式求解是重要考点之一，为了让学生掌握并运用好数形结合思想，笔者深入归纳总结了数形结合思想在高中数学不等式求解中的一些应用方法，希望高中学子能够运用好数形结合思想。

关键词：高中数学；数形结合；解题方法

中图分类号：G633.6文献标识码：A文章编号：1992-7711（2020）10-0136

一、数形结合思想概论

数学的起源就是古人研究的数形关系，数和形是数学研究的基本对象，其在某些条件下可以互相转换。在高中数学中，也是研究数形的关系，而数形结合就是数与形的关联。数形结合是一种数学思想，其有两种模式：一是使用数来阐述形的特点和属性，二是使用形来直观地表示数之间的关系。

在高中数学中运用数学思想的解题方法主要在三个方面。1.运用数形结合思想解决函数问题。2.运用数形结合方法解决不等式问题。3.运用数形结合解决平面几何问题。前两种都是用形来直观表示数之间关系的数形结合思想，第三种是使用数来阐述形的属性特点。

二、数形结合思想解决不等式问题

在不等式问题中运用数形结合来解答，可以避免复杂的分类讨论，简化题目，直接利用几何图形特点得出答案。

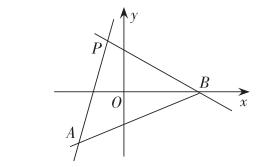
例题一：设有关于x的不等式|x-3|+|x-4|

解：设函数f（x）=|x-3|+|x-4|，函数g（x）=a，在平面直角坐标系中作出函数f（x）和g（x）的图像如下。

由函数f（x）和g（x）的图像特征可得要使|x-3|+|x-4|

所以可得a的取值范围为（-∞，1]。

例题二：设函数f（x）=x2-2ax+2，并且x∈[-1，+∞）时，f（x）≥a恒成立，求a的取值范围。

解：由f（x）≥a可得x2-2ax+2≥a即x2+2>a（2x+1）。

设函数f（x）=x2+2，函数g（x）=a（2x+1），作出函数f（x）和函数g（x）的图像：

由函数图像特征可得a的取值范围为图中直线斜率的取值范围。

即a∈（-3，1）。

三、数形结合思想解决平面解析几何问题

在高中数学中，平面解析几何知识是运用到数形结合思想最广泛的知识点，在直线斜率、直线与圆、直线与圆锥曲线等问题上，运用数形结合思想解题是最为简洁的。

例题一（直线斜率问题）：直线L过点P（-1，2），且与点A（-2，-3）、B（4，0）为端点的线段AB相交，求直线L的斜率的取值范围。

在解这类题目时，先作出函数图形：

计算直线pa的斜率k（pa）=5，直线pb的斜率k（pb）=2/5。

由函数的图像特征可得k≥5或k≤2/5。

例题二（直线与圆问题）：设圆O的方程为x+y-2x+4y+4=0，直线L的方程为3x-4y+9=0，求圆O上的点P到直线L上的最大距离为多少。

在解这类问题时，运用数形结合思想能使问题得到迅速解决：

将圆的方程配方可得（x-1）2+（y+2）2=1，由此可得圆心O为（1，-2），半径r=1。

由直线与圆的图形特征可得：圆到直线的最大距离=圆心到直线的距离+半径。

圆心O到直线L的距离d=4，由上式可得直线L到圆O的最大距离为d+r=4+1=5。

参考文献：

[1]卢向敏.数形结合方法在高中数学教学中的应用[D].内蒙古师范大学，2013.

[2]韩雪丽.数形结合思想方法在高中数学教学中的研究与实践[D].辽宁师范大学，2013.

[3]孔令偉.数形结合思想方法在高中数学教学与解题中的应用[D].辽宁师范大学，2015.

（作者单位：甘肃省张掖市山丹第一中学734000）