例析“图形与几何”里的代换思想

周建平

摘要：代换思想是把一个量用与它相等的另一个量替代，使问题简单化，进而解决问题。本文结合长度代换、面积代换、体积代换这三个方面的实例，分析了小学数学“图形与几何”领域里代换思想解决问题的途径。

关键词：代换思想   长度代换   面积代换   体积代换

近年来，在小学数学课堂教学中，代换思想占有一席之地，得到广泛应用。下面，笔者结合例题，分析在小学数学“图形与几何”领域中，使用代换思想解决问题的方法。

一、长度代换例析

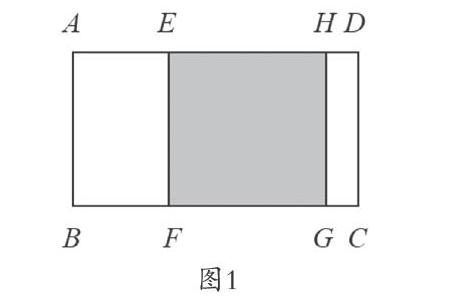
例1：如图1所示，阴影部分是正方形，AH=8厘米，DE=6厘米，求大长方形ABCD的周长。

分析：学生初读题时会觉得缺少条件，因为计算长方形的周长，一般要已知长和宽，但本题中的已知条件只有两个，AH=8厘米，DE=6厘米，是求不出长方形的长和宽的。

从“整体”考虑，长方形周长公式是周长=（长+宽）×2，学生只要知道“长+宽”，就可以求出周长，而不需要知道长和宽是多少。

AH、DE两段的长度包括了中间的EH，如果把AH、DE这两段长度加起来，相当于AE+EH+EH+HD。在计算中，EH被重复相加，即AH+DE=AD+EH，AD为大长方形的长，EH为正方形的边长，而这个边长正好是大长方形宽的长度，也就是说8+6所得到的长度是长方形周长的一半，这时再乘以2，就可以得到整个长方形的周长为28厘米。

二、面积代换例析

例2：如图2所示，大正方形面积比小正方形面积大10平方厘米，求阴影部分的面积。

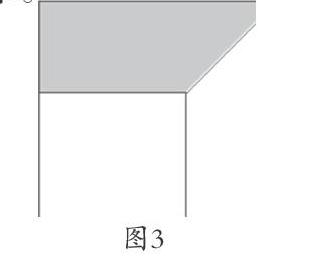
分析：本题阴影部分是一个梯形，求它的面积。按一般求法，学生要知道梯形的上底、下底、高，但题目中没有出现;如果看成两个三角形，仍找不到底和高各是多少。这时候，学生需要变换思路。如图3所示，我们可以将小正方形移动到大正方形内，图2和图3中的阴影部分都是梯形，上底、下底和高都分别对应相等，两个阴影面积相等。

如图3所示，阴影部分同右下部分的梯形形状、大小一样，而这两部分的面积之和（阴影面积的两倍）正好是大正方形面积减去小正方形面积的差，即已知条件的10平方厘米，所以阴影面积为10÷2=5平方厘米。

我们无法根据梯形面积公式或三角形面积公式直接求出本题所求阴影部分面积，但运用了代换思想，并通过位移正方形，用与它上底、下底和高分别对应相等的梯形进行代换，学生就能解决问题了。

三、体积代换例析

例3：一个饮料瓶的下方是圆柱形，把300毫升的水倒进去，正放时，水的高度是12厘米（如圖4所示）;密闭后倒放时，空余部分的高度为8厘米（如图5所示）。这个饮料瓶的容积是多少毫升？

分析：不管瓶子是正放还是倒放，瓶子的容积始终不变，瓶子里水的体积不变，剩余部分容积也不变。倒放时，剩余部分加正放时水的体积之和是整瓶的容积。

如果把图5下方的水换成图4下方的水，则可以画出图6。

由图6可以看出，水的体积占整瓶容积的，也就是。由此可答，=，300÷=500毫升。

根据密闭状态下水的体积不变，利用代换思想，用图4下方水的体积代换图5下方水的体积，与图5上方剩余部分构成一个圆柱形，再用比例求解。

代换思想是小学阶段的重要数学思想。在教学中，教师要引导学生在观察中思考，指导学生用一个与它相等的量代换另一个量，达到巧解问题的目的。

（作者单位：江西省丰城市剑光第五小学）