J对称分块算子矩阵的谱

钱志祥

(广东理工学院基础教学部， 广东 肇庆 526100)

引 言

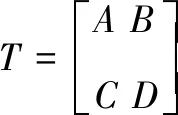
1 预备知识

定义1[14]总假定X是Hilbert空间，则正交直接和X×X也是Hilbert空间，不产生混淆的前提下空间X和X×X的内积都记为(·,·)，对任意x∈(x1,x2)T，y∈(y1,y2)T∈X×X的内积定义为：

(x,y)(x1,y1)+(x2,y2)

(1)

令Ai,Bi,Ci,Di∈B(X),则

且对任意α∈C和x∈(x1,x2)T∈X×X,定义：

(2)

常数和分块算子矩阵的乘积，定义为：

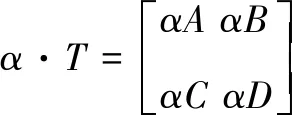
(3)

两个分块算子矩阵的和规定为：

(4)

两个分块算子矩阵的积规定为：

(5)

零空间为

Ν(T)=

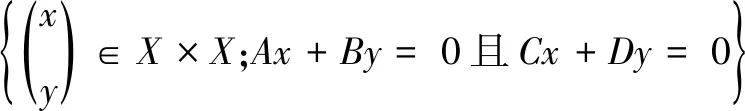
(6)

值域为

R(T)=

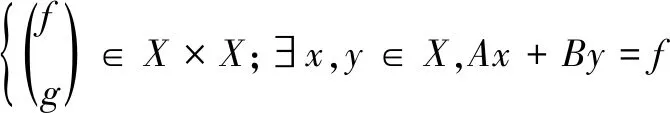
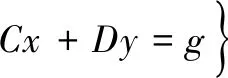
(7)

定义2[15]设X是复的可分Hilbert空间，J表示X上的复共轭算子，即∀x,y∈X,(Jx,Jy)=(y,x)，而且具有如下性质：

J(x+y)=Jx+Jy

(8)

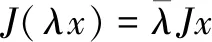
(9)

J2x=x

(10)

定义3[15]设T是定义在Hilbert空间X上的稠定线性算子，若∀x,y∈D(T)，有(Jx,Ty)=(JTx,y)，则称算子T是J对称算子。

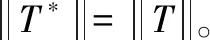
由定义容易发现，T是J对称算子的充要条件即JT⊂T*J(T⊂JT*J,或JYJ⊂T*)。

定义5[15]如果JT=T*J(T=JT*J,或JTJ=T*)，则称算子T是J自伴算子。

定义6[15]对于定义在Hilbert空间X上的闭稠定线性的算子T，若对任意λ∈C，存在常数K=K(λ)>0，使得对所有

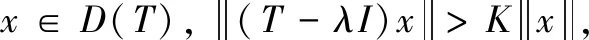
则称数λ为算子T的正则型点，T的所有正则型点的全体称为算子的正则型域，记为Π(T)，即：

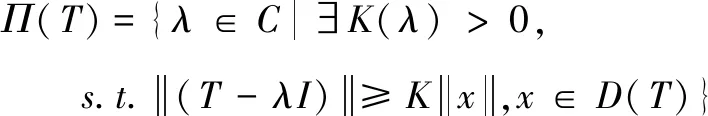
(11)

而σK(T)=CΠ(T)称为算子T的谱核。

定义7[15]记m(λ)=dimR(λI-T)⊥=def(T,λ)=dim(XRλ(T))，m(λ)是一个常数，它称为算子T的亏数，若T是定义在Hilbert空间X上的一个稠定的J闭对称的算子，且Π(T)≠Φ，称亏数m(λ)为算子T的亏指数，记为d(T)。

定义8[15]记Nλ(T) 和n(λ)分别表示算子T-λI的零空间和其零空间的维数，即

n(λ)=dimNλ(T)=dim ker(λI-T)=

dim{f|(T-λI)f=0,f∈D(T)}

(12)

2 主要结论

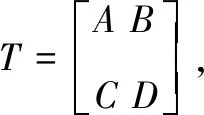
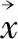
(13)

又因为

(14)

比较式(13)和式(14)得：

当A,B,C,D是J对称的且B=C时，有(Tx,y)=(x,JTy)，则T是J对称的。

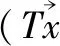
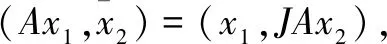
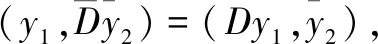
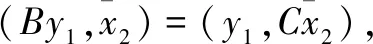
所以(Cx1,Jy2)=(x1,JBy2)所以B=C且是J对称的。

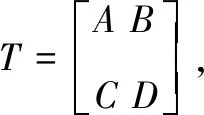
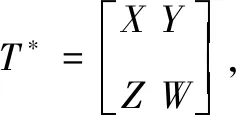
即

(15)

(16)

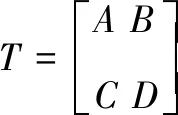
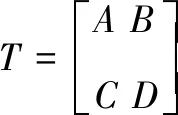
所以

JA⊂A*JJB⊂C*JJC⊂B*JJD⊂D*J

(17)

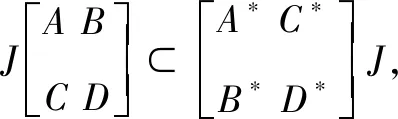
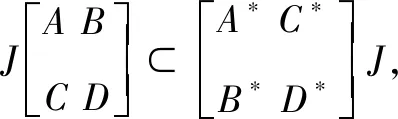
JA⊂A*JJB⊂C*JJC⊂B*JJD⊂D*J

(18)

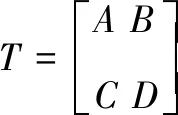
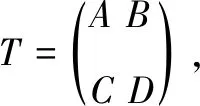
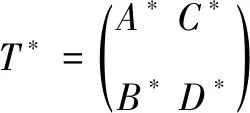
(19)

所以，A=JA*J,B=JB*J,C=JC*J,D=JD*J，所以A,B,C.D均是J自伴算子且B=C。

反之，当A,B,C,D均是J自伴算子且B=C时，有：

A=JA*J,B=JB*J=C=JC*J,D=JD*J

(20)

于是

(21)

即T=JT*J，因此，T是J自伴算子。

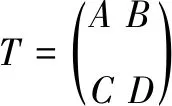
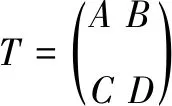
且B=C，A=JA*J,B=JB*J,C=JC*J,D=JD*J。

故

JAJ=A*,JBJ=B*,JCJ=C*,JDJ=D*

(22)

(23)

T=JT*J=JJT*JJ=T**

(24)

T**=JT*J

(25)

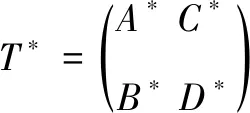
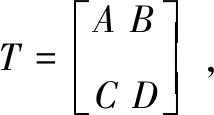
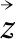
(26)

于是

(27)

于是

所以

(29)

这表示

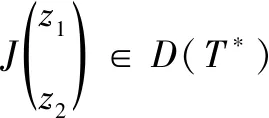
即：

(30)

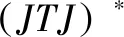
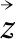
(31)

(32)

这表示：

(33)

即有JT*J⊆(JTJ)*，所以，(JTJ)*=JT*J

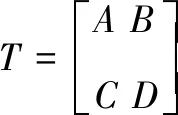
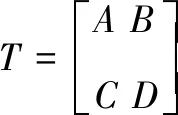
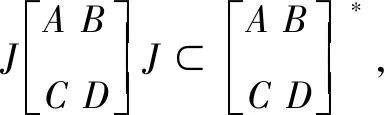
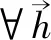
(34)

即

(35)

所以

(36)

从而

(37)

即

(38)

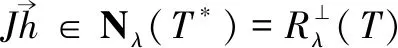
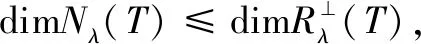
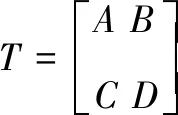
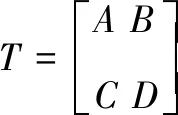
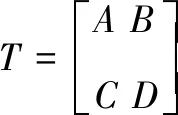
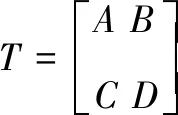
(39)

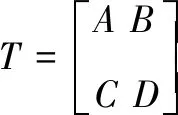
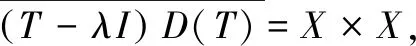
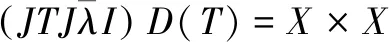
(40)

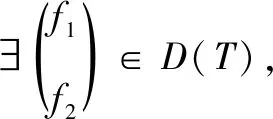
(41)

根据(40)式可知，

使得

(42)

由引理3知T是J对称算子，所以式(42)可表示为：

(43)

根据式(41)和式(43)得：

(44)

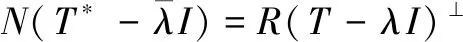
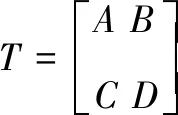
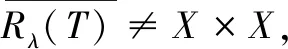
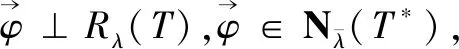
(45)

由引理5知T*也是J自伴算子，T*=JTJ，故

(46)

可以导出

(47)

即

(48)

所以λ∉σr(T)，这与λ∈σr(T)矛盾，故σr(T)=Φ。

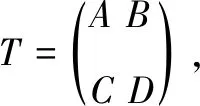
3 结束语

本文主要研究了Hilbert空间中J对称有界2×2分块算子矩阵的谱，将进一步开展对于Hilbert空间中J对称无界2×2分块算子矩阵的谱方面的研究。