盾构隧道竖井内油气管道流固耦合振动特性分析

孔令钱， 唐怀平， 陈荟键， 肖骁千里

(西南交通大学力学与工程学院， 成都 610031)

引 言

管道输送是油气资源长距离运输使用的主要手段[1]，油气管道在途经河流时经常采用盾构隧道进行穿越。管道内流体介质与管道之间的耦合作用[2]是引起油气管道振动的重要原因之一。油气管道在长期运行中，当内部流体介质或者加压泵的激励频率与管道的固有频率相近时，就会使油气管道振动加剧，从而引起管道和附属设施的疲劳破坏[3]。因此，对油气管道的流固耦合振动特性和机理进行系统研究具有重要意义。

近年来，许多学者都对输送流体管道的流固耦合振动特性进行了研究。齐欢欢等[4]研究了Galerkin模态截断对计算悬臂输液管道固有频率的影响，发现通过截取适当的模态能够建立比较精确地反映真实系统动力学特性的低阶模型。刘昌领等[5-7]利用哈密顿变分原理建立发动机燃油管路流固耦合振动控制方程，研究了临界流速和临界压力与流体流速和压力之间的关系，结果表明管路系统的临界流速和临界压力随着流体流速和压力的增大而降低。权凌霄等[8-9]对液压管路系统流固耦合振动特性进行分析，研究了管材参数对管路系统固有频率的影响。俞树荣等[10-12]对流体脉动压力作用下的弯曲输流管道进行了仿真模拟，研究了管道内流体脉动频率对管道位移振幅的影响，模拟结果表明当流速一定时，流体的脉动频率与管道的固有频率越接近，弯管的位移振幅越大。徐凯等[13]对油气直管道的模态进行了模拟计算，计算结果表明油气直管道在其低阶模态上表现了较为整体的振型，而在较高的频段内则显示出了大量的局部模态。

但以上研究大都是针对输送航空燃油或者液压油的小管径管道，或者是仅考虑了管道内部流体对管道固有特性的影响，而针对水下环境中输送油气资源的大管径薄壁管道流固耦合振动特性的研究还很少。本研究应用有限元软件ANSYS Workbench平台，采用直接耦合方法对某盾构穿越隧道竖井内油气管道结构的模态进行模拟和计算。仿真模拟中主要考虑了管道内部流体和管道外部静水与管道的耦合作用、管道固定导向支座、管道壁厚和管道内部流体介质密度对油气管道固有特性的影响。研究得出的结论可以为相关类型盾构穿越隧道竖井内油气管道的安装与振动控制提供一定的参考。

1 直接耦合有限元方法

在考虑流体与固体相互作用的直接耦合有限元方法中，流体的运动方程通常采用压力作为基本变量，结构的运动方程则采用位移作为基本变量，在流体与结构交界处，通过边界条件将流体运动方程与结构运动方程耦合起来。

在油气管道中，内部流体介质的平均流速远小于声速，平均流速的影响可以忽略[14]，近似认为流体平均密度是不变的，此时流体的波动方程可以表示为

(1)

采用Galerkin方法对流体域进行离散化并对整个流域进行积分[15]，结合在流固交界面、刚性壁面和无限远处的边界条件，得到离散形式的流体运动方程，表示成矩阵形式为

(2)

式中：下标F表示流体，ρ表示流体的密度；p表示流体的压力矢量；u表示结构的位移矢量；MF表示流体的质量矩阵；CF表示流体的阻尼矩阵；KF表示流体的等效刚度矩阵；B表示流体与结构的耦合矩阵。

流体与结构在交界处存在耦合效应，对结构产生一个作用力，根据虚功原理将流体微元产生的分布面力等效到结构单元节点上[16]，通过坐标变换并写成矩阵形式为

(3)

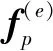
考虑流体对结构的作用力，则结构运动方程可以表示为

(4)

式中：下标S表示结构，MS表示结构的质量矩阵；CS表示结构的阻尼矩阵；KS表示结构的刚度矩阵；FS表示结构的外载荷矢量。

将式(2)和式(4)联立并写成矩阵形式，得到流体与结构耦合的有限元运动方程为

(5)

在实际分析中，若不考虑阻尼效应及结构外载荷作用，则方程(5)可以进一步简化为

(6)

2 流固耦合有限元模型

某盾构穿越隧道竖井内油气管道材料为X80管线钢，管道外径D为1219 mm，壁厚为27.5 mm，设计输送压力为10 MPa，运行温度为30 ℃，整个竖井在运行状态下采用静水密封，模型中各材料参数如表1所示。由于管道在隧道内外存在一定的高度差，因此竖井内管道安装时采用两段半径R=6D的60°热煨弯管，中间用长度为1000 mm直管进行连接的方式，如图1所示。

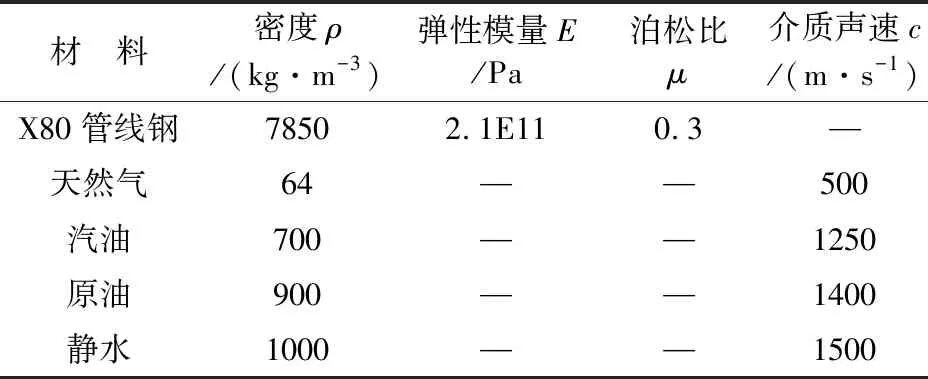
表1 模型中各材料参数

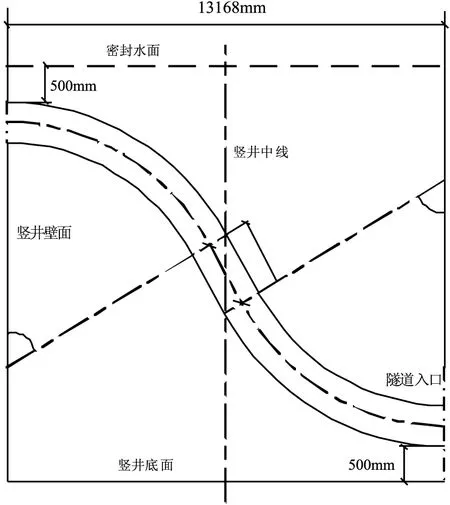
图1 盾构隧道竖井内管道安装示意图

首先在Creo软件中通过扫描方式建立管道的三维实体模型，导入ANSYS Workbench平台，采用Fill命令对管道内部进行填充，建立管道内部流体模型，同时把管道与内部流体合并成一个整体，从而保证划分网格时流固交界面上的网格节点重合[17]。选择扫掠方法对管道和内部流体进行网格划分，管道采用Solid186三维实体单元，内部流体采用Fluid220三维声学流体单元。Fluid220是20节点高阶单元，每个节点包含三个位移自由度和一个压力自由度，用于模拟流体内部时，只有压力自由度有效，用于模拟流体与结构边界时，位移自由度和压力自由度都有效。划分网格后的有限元模型如图2所示。

图2 模型网格划分

其次设置模型边界条件。将内部流体标记为Acoustic Body，定义流体的密度、流体介质中的声速以及重力加速度的大小和方向。将内部流体与管道的交界面标记为FSI Interface，使内部流体与管道在边界处的单元位移保持一致，不会出现流体与结构分离。竖井内管道约束方式主要有锚固墩和固定导向支座两种，锚固墩能够限制管道所有的位移和转角，可以视为固定约束。固定导向支座如图3所示，除了能够支撑管道重量，还能限制管道径向位移，但不能限制管道轴向位移。

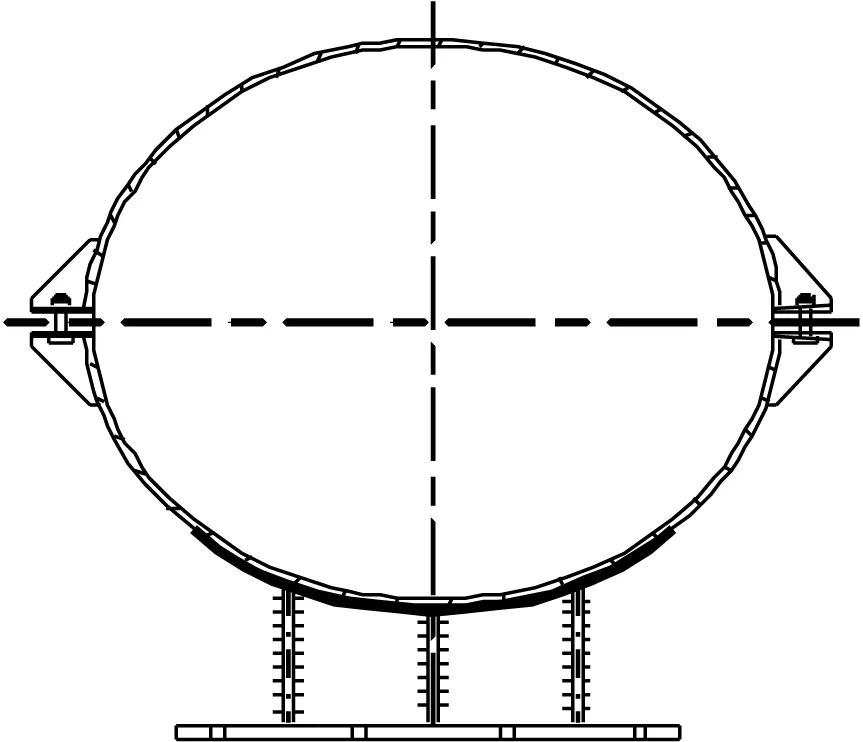
图3 固定导向支座

3 模拟结果分析

3.1 流固耦合作用影响

在ANSYS Workbench平台中，利用Modal模块和Acoustic Extension扩展插件对油气管道的结构模态进行计算。为了对比管道内部流体和管道外部静水对管道结构模态的影响，在考虑管道两端均为锚固墩约束，输送介质为天然气的情况下，分别对无耦合、天然气-管道二者耦合、天然气-管道-静水三者耦合的管道结构模态进行计算。管道的前6阶固有频率见表2。

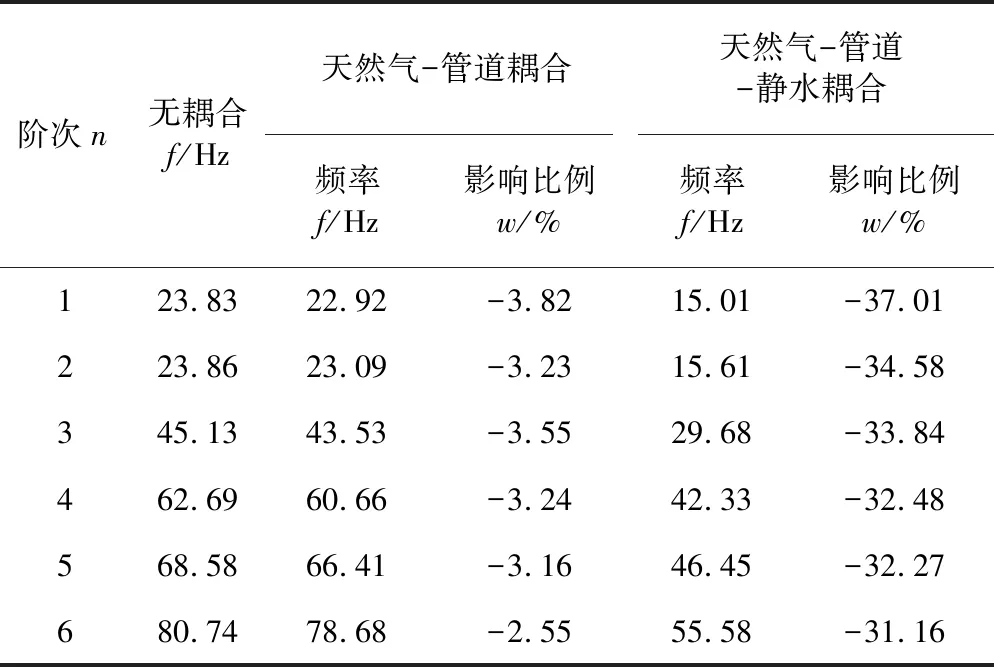
表2 不同耦合下管道的固有频率

从表2可以看出，管道内部天然气和管道外部静水与管道的耦合作用均使油气管道的前6阶固有频率降低，随着阶数的增大，固有频率降低的比例逐渐减小。天然气-管道二者耦合作用导致油气管道固有频率降低的最小幅度为2.55%，最大幅度为3.82%，天然气-管道-静水三者耦合作用导致油气管道固有频率降低的最小幅度为31.16%，最大幅度为37.01%。因此内部天然气流体对油气管道固有频率的影响较小，外部静水对油气管道固有频率的影响较大，其影响不可忽略。

天然气-管道-静水耦合管道结构的前6阶模态振型如图4所示。从图4可以看出，天然气-管道-静水耦合管道的前2阶模态振型为横向弯曲振动形态，第3阶模态振型为扭转振动形态，第4阶至第6阶模态振型均为壳式振动形态。管道前5阶模态振型反映管道整体结构振动，第6阶模态振型出现了局部振动形态，主要发生在两段弯管的位置，因此管道在弯管处存在刚度不足的问题，更容易造成管道的疲劳破坏。

模拟结果对比表明，考虑内部天然气流体和外部静水与管道耦合作用的油气管道模态振型与不考虑耦合空管道的模态振型(图略)基本一致，因此管道内部流体和管道外部静水与管道的耦合作用对管道的模态振型影响甚微。

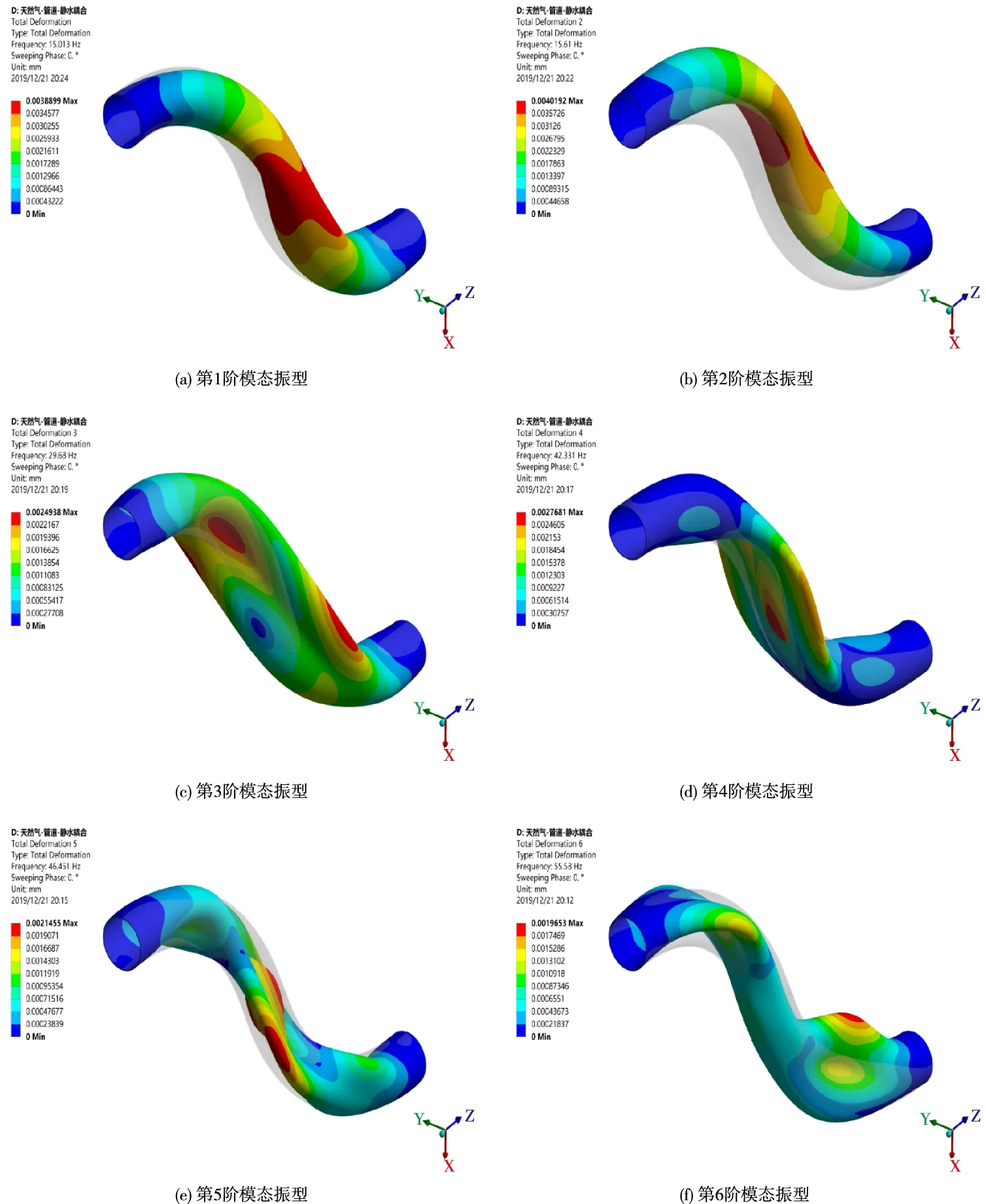
图4 天然气-管道-静水耦合的管道前6阶模态振型

3.2 固定导向支座影响

油气管道在竖井内远离盾构隧道入口处一般采用锚固墩约束，而在隧道入口处采用锚固墩或者固定导向支座约束。为了对比管道支座对油气管道固有频率的影响，在考虑输送介质为天然气的情况下，分别对隧道入口处采用锚固墩约束和固定导向支座约束的管道结构模态进行计算，得到管道结构的前6阶固有频率见表3。

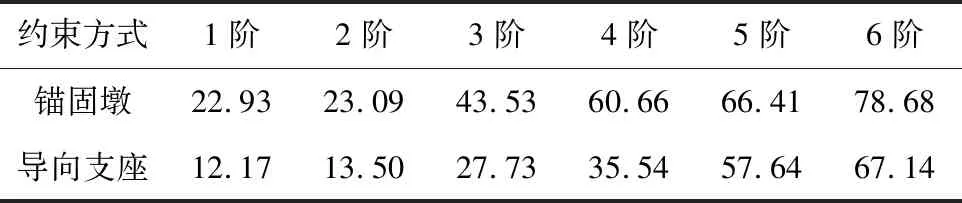
表3 不同约束下的管道固有频率(Hz)

从表3可以看出，油气管道采用一端锚固墩一端固定导向支座约束时的固有频率明显低于两端都采用锚固墩约束时的固有频率。固定导向支座对管道的前4阶固有频率影响较大，对第5、6阶固有频率影响较小，原因在于固定导向支座相当于降低了管道结构整体刚度，对梁式振动影响更为明显。

3.3 管道壁厚影响

为研究管道壁厚对油气管道固有频率的影响，考虑管道的两端均为锚固墩约束，输送介质为天然气的情况下，分别对管壁厚度为27.5 mm、32.5 mm、37.5 mm和42.5 mm的管道结构模态进行计算，得到管道的前6阶固有频率变化规律如图5所示。

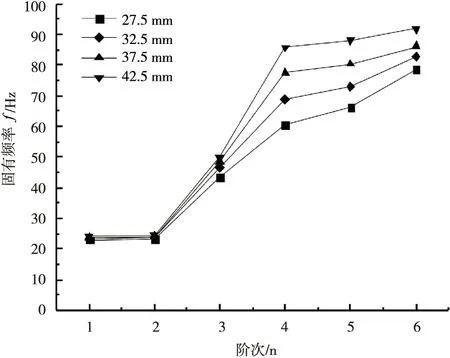
图5 不同壁厚下管道的固有频率变化

从图5可以看出，油气管道的固有频率随着管道壁厚的增大而增大。管道壁厚对梁式振动频率的影响较小，对壳式振动频率的影响较大，因此壳式振动比梁式振动对管道壁厚引起的管道结构刚度变化更敏感。

3.4 输送介质密度影响

为研究管道内部输送介质密度对油气管道固有频率的影响，考虑管道的两端均为锚固墩约束的情况下，分别对内部输送介质为天然气、汽油和原油的管道模态进行计算，得到管道的前6阶固有频率变化规律如图6所示。

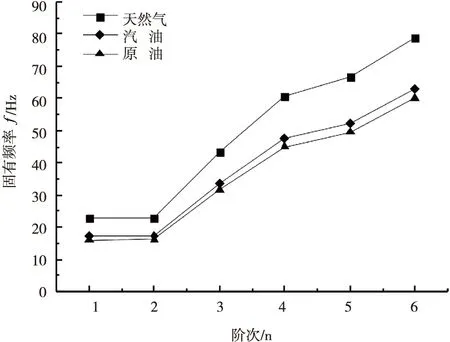
图6 不同输送介质下管道的固有频率变化

从图6可以看出，油气管道的固有频率随着输送介质密度的增大而减小。输送汽油和原油管道的固有频率明显低于输送天然气管道的固有频率，表明汽油和原油与管道的耦合作用大于天然气与管道的耦合作用，原因在于相同体积的液体附加质量远大于气体附加质量，输送液体的管道显得更“柔”，从而管道的固有频率更低。

4 结 论

对某盾构穿越隧道竖井内油气管道的振动特性进行模拟计算和分析，考虑不同因素对油气管道固有特性的影响，得出结论如下：

(1)内部流体介质和外部静水与管道的耦合作用均降低油气管道的固有频率，外部静水对油气管道固有频率的影响较大，固有频率降低明显，而流固耦合作用对管道的模态振型没有影响。

(2)油气管道的低阶模态振型属于梁式振动形态，高阶模态振型属于壳式振动形态，并且在弯管位置出现了局部振动形态。

(3)管道支座对管道的固有频率有影响，固定导向支座对油气管道梁式振动的影响较大，其固有频率明显减小。

(4)油气管道的固有频率随着管道壁厚的增大而增大，随着输送介质密度的增大而减小，其中管道壁厚对油气管道壳式振型固有频率的影响明显。