基于线性规划的工程投资分配模型及优化

高兰芳

(福建船政交通职业学院, 福州 350007)

引 言

随着经济全球化进程的不断推进以及互联网科技的迅猛发展，工程投资企业在进行投资决策时所面对的不确定性越来越大。随着经济发展进入新常态，日益增长的公共产品需求与供给之间缺口不断扩大，PPP投融资模式的出现体现了资金分配的重要性[1]。如何进行资本结构优化对于工程投资企业来说具有无比重要的意义。工程投资企业涉及前期的主要问题是项目投资决策，投资决策中需要解决的一个主要问题是资金最优分配问题。资金分配，顾名思义就是在资金总量不变的情况下，通过统筹安排，对各种项目方案所需的资金进行合理分配，以期达到投资的最大收益。以往对于此类经济决策问题，传统方法是通过经济评价指标来进行评判。经济评价指标主要包括内部收益率、净现值等，随着净现值法的日益推广，成为目前最广泛的投资预算决策方法，而净现值法过于追求利益最大化，而未能充分考虑资金的利用率问题，更适合资金无限或者资金充足的前提情况下进行判断。在投资资金有限的前提条件下，如何利用有限的资金谋求净现值最大化成为投资决策者需要解决的首要难题。为了解决资金有限前提下项目投资分配抉择难题，本文将投资决策的经济学问题转化成线性规划中的资源配置问题，以收益最大化为目标，建立模型求出最优解，以单纯形方法为基础使用MATLAB进行编程求解，最后结合具体实例进行分析。

线性规划的概念是于1947年军事行动计划中产生的，发展至今已有近100年的历史，线性规划方法用于工程设计也被称为“最优化方法”，已成为工程技术中的一个有力的研究工具，也是西方计量经济学派常用的数学工具。著名的单纯形方法是Dantzing于1947年提出的求解线性规划问题的方法，基于该方法，随着研究问题的不断深入，又相继出现了对偶单纯性法。

现行的投资决策方案评价方法分为贴现的方法和非贴现的方法两类。常规贴现方法包括:净现值法、净现值指数法和内部收益率法，其中净现值指数法和净现值法的基本原理相同。只是前者相对于后者多考虑了资金的利用率水平。非贴现方法即不考虑资金时间价值的方法，适用于静态评价，对方案资金的使用价值欠缺充分考虑，只能作为参照指标，不能作为绝对指标。管超，张则强[2]等基于多目标规划，提出了多行设备布局的一种多目标差分进化算法和线性规划混合方法；苏志雄，魏汉英[3]等研究了资源受限条件下施工平行工序顺序对优化的0-1规划模型；林浩楠[4]针对传统算法提出了基于多目标遗传算法和深度学习的面向多个投资机器人的资金分配算法；赵培玲，周根宝[5]基于人工鱼群算法针对多投资项目资金分配问题进行建模分析,对此问题进行了编程实现；任华茜[6]根据房地产项目开发的特点,给出了同时考虑项目成本收益,资金成本,资金归还问题的项目多阶段资金分配模型。国内诸多研究成果中，第一类是完全在理论条件下的资金模型分析，虽然全面具体，但是难以直接运用于实际；第二类通过0-1线性规划来选择项目，只适用于在项目方案选择或者放弃条件下运用，同时也未考虑资金的时间成本。

综合国内外研究成果可以发现，当前对于“选择谁”的问题研究已经较为成熟，而在投资决策问题中仍然存在的“遗憾”，主要是对于选择出的方案应当如何给出投资比例的问题。在项目投资决策中，投资决策给出的方案往往可以多种方案并行，如何把控投资分配比例，成为研究的主要问题[7]。因此，为了建立一个更贴近实际并且能更好规避风险的资金分配模型，本文提出的解决办法是应用线性规划中的资源配置解决办法，将投资资金按照一定比例分配到各个项目当中。

1 投资最优资金分配模型的构建

1.1 模型假设

民营工程投资企业，诸如房地产公司、施工企业等在进行投资决策时盈利是其考虑的首要目标。在合理使用资金的前提条件下以最大盈利为目标来进行投资分配比例的划定。盈利指标一般选择净现值指标来衡量。模型数据选取所有可行的投资方案并获得其一定年限内的成本、盈利以及各年限内工程投资企业可用于投资的资金。其中，可行的投资方案是指通过风险控制部门评估合格后可实施的方案。模型选取项目年限设定为5年，一方面随着科技发展，关于各类型方案的风险数据会越来越完善，数据也会越来越准确，同时越来越多的风险因素不允许管理者做出更长时间的规划；另一方面，更加符合中国各期五年投资计划的国情，更容易贴合国家方针政策的引导，有利于各期项目发展。研究的前提为无风险因素的确定型风险投资决策问题，所以假设各方案各期的成本与盈利可以通过类似项目调查法由专业的评估部门得出结果，公司各期可用资金则可通过公司的财务计划可以获得。

1.2 不同资金模式下线性规划模型的建立

本文主要考虑无风险因素的确定型投资分配线性规划模型，即确定型决策问题。根据决策者面临的不同决策环境，即决策结果确定与否及是否明确了任务的结构，将决策分为不确定型决策和确定型决策[8]。在确定型决策条件下，所进行的投资分配模型不需要考虑其他风险因素。当有风险因素存在时，受风险因素影响，某些参数如项目某一期的投资成本、某项目某一年的利润等将具有极大的不确定性，将这种不确定性量化后得到的往往是非线性关系。工程投资企业的主要资金来源包括自有资金、吸收资金、专项资金3个部分组成[9]。自有资金是指工程投资企业内部积累或者国家拨款，可用于自身正常经营活动，不需要偿还的一种资金类型，与自有资金相对的是吸收资金。吸收资金也就是借入资金，主要是指工程投资企业为了周转或者扩大生产，依法向金融机构借入并且到期后需要偿还利息的一种资金。本文分别研究含有这两种不同资金来源时的投资分配模型。

1.2.1 完全自有资金投资分配模型

假设工程投资企业的全部投资资金来源均为自有资金，即将可利用的资金A看作1种资源，并将这种资源分别分配到若干种项目投资方式B1...Bm中；每种投资项目分n期投入建设，各期的资金投入量见表1，记为b11...bij(i=1,...,n;j=1,...,m),每年的投资限额为a1...am,投资方式B1...Bn，各年的利润价格记为c1...cm。假定各期的投资比例固定，且投资比例与盈利比例相同。

表1 工程投资企业投资项目有关参数表 单位：万元

对于工程投资企业而言，在资金有限的前提下，如何利用有限的资金追求最大利润通常是工程投资企业的目标。在项目投资决策中，通常利用净现值指标来衡量工程投资项目的经济可行性，净现值越大则说明项目的盈利能力越强[10]。

在资金有限的前提下，各项目方案可以认定为独立型方案，即各项目之间现金流量互不影响，其中任一投资项目的选择与否对于其他项目的投资没有影响[11]。考虑资金的时间价值影响，假设基准收益率为q，设各项目资金的投资分配比例为x1...xn,由于工程投资企业的目标是使盈利的净现值NPV最大，则有目标函数如式(1)所示：

(1)

对于约束方程，提出两种假设。

假设一：每一期的投资资金只能用于该期，则有约束方程为：

(2)

假设二：每一期多余的投资资金可用于下一期，则有约束方程为

(3)

其中：

利润的净现值为

NPVi=ci(P/A,q,i)

(4)

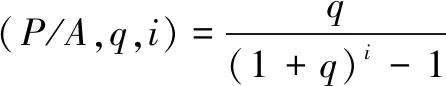
(5)

式中：i=1,...n,表示投资期第i年；j=1,..n,表示第j个项目；P表示现值，A表示年值,ci表示每年利润值，q表示折现率。折现率取值不同会直接影响工程投资项目净现值分析的结果，有关部门统一发布的社会折现率不能反映不同地区不同项目之间的差别[12]。目前国内采用固定折现率，即固定折现率对未来现金流折减过多，不利于远期效益高的项目，也不符合不同地区经济发展水平，对于长期项目更适合采用递减折现率[13]。

1.2.2 含有借入资金的投资分配模型

在现实生产活动中，工程投资企业的自有资金常常不足，需要通过向银行等金融机构合法的借入资金用以投资周转。假设某工程投资企业拥有自有资金A，借入资金B，每期可借入的资金限额为D,现将自有资金A和借入资金B分m期进行投资，假设共有可行的投资项目共N个，记为K1、K2...Kn,每期计划可用限额分别为W1、W2...Wm,仍然以最大盈利的净现值为目标，假设每期投资的比例分别为x1,x2...xm。

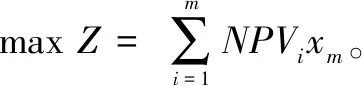
假设每期借入的资金在下一期还本付息，资金只能在当年使用，可以建立如下的约束方程：

(6)

综上所述，可以得出只在当年使用借入资金的资金分配模型为：

(7)

假设当年资金可用于下年投资，则有资金分配模型为：

(8)

1.3 模型的求解

投资分配模型求解的主要方法是单纯形法，通过MATLAB工具进行编程解决，其基本步骤为：首先，引入松弛变量，将线性规划方程改写成标准型；其次，以标准线性规划方程为基础，写出初始单纯形表；最后，将初始单纯形表输入MATLAB程序，迭代运行至最优解，则最优解mbhs、x1、x2、x3就是所求的最优资金分配比例。

2 实例分析

2.1 完全自有资金的投资资金分配

某部门在今后五年可用于投资的资金总额为37万元，有三个可以考虑投资的项目。假定每个项目可以按比例进行投资，但是每一期比例均相同。三个项目分为5期进行，各期所需资金以及预计盈利，假设基准收益率为10%，见表2。

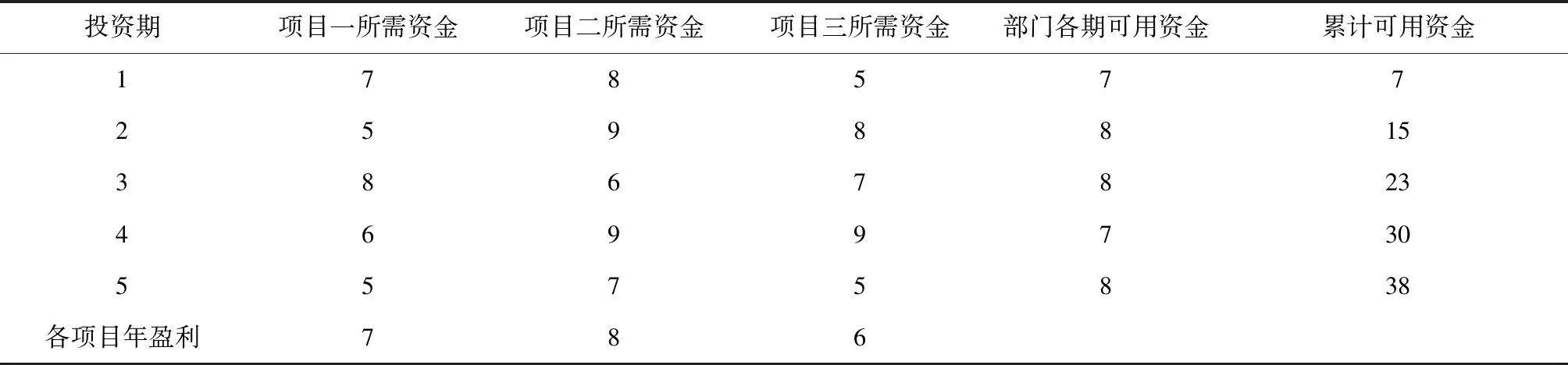
表2 工程投资企业投资项目参数表 单位：万元

①现值的计算

根据表2以及式(4)和式(5)可以得到各项目5年盈利的净现值，见表3，结果保留两位小数。

表3 项目盈利净现值表 单位：万元

②目标函数及约束方程的的建立

根据本例内容，设投资分配比例分别为x1、x2、x3,假设每一期多余的资金不可用于下一期，将数据代入公式(2)，则有如下的线性规划方程：

(9)

引入松弛变量x4、x5、x6、x7、x8，将方程改写成标准型，改写后的线性规划方程如下：

(10)

该方程的初始单纯形表见表4。

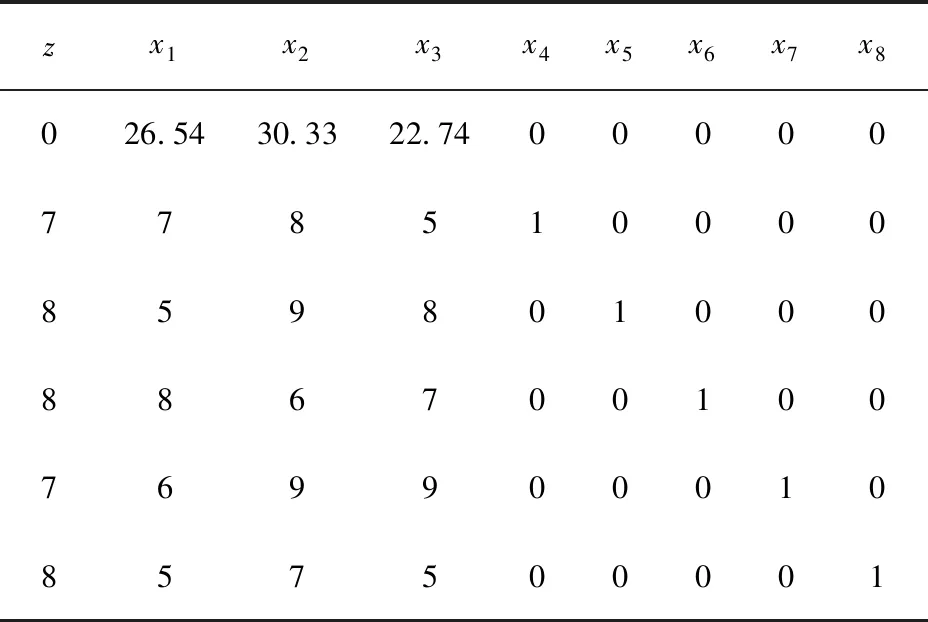
表4 初始单纯形表——多余的资金不可用

将初始单纯形表输入根据单纯形法编制的MATLAB程序，得到mbhsz=27.2165，x1=0.7886,x2=0.0732，x3=0.1789,也即当对项目一的投资比例为0.7945，对项目二投资比例为0.0732，对项目三的投资比例为0.2877时，可以获得最大收益净现值为27.2165万元。

当每一期剩余资金可用于下一期投资时，将数据代入式(3)，形成新的线性规划方程为：

将该线性规划方程写成标准形式有：

对于该方程有初始单纯形表见表5：

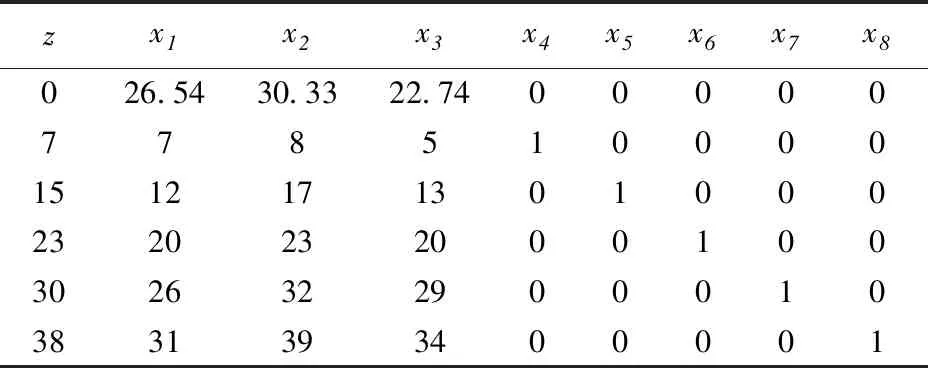
表5 初始单纯形表——多余的资金可用

由MATLAB程序计算，可以得到mbhsz=27.9910，x1=0.7260,x2=0，x3=0.3836,也即当对项目一的投资比例为0.7260，对项目二不投资，对项目三的投资比例为0.3836时，可以获得最大收益净现值为22.9910万元。

2.2 含有借入资金的投资资金分配

某部门在今后五年可用于投资的自有资金总额为37万元，有三个可以考虑投资的项目。假定每个项目可以按比例进行投资，每一期比例均相同且获得收益的比例与投资比例相同。三个项目分为5期进行，每期均可借入资金用于投资，假设每期借入资金在下一期还本付息，每期借入资金金额及各期所需资金以及预计盈利，见表6。假设基准收益率为10%。

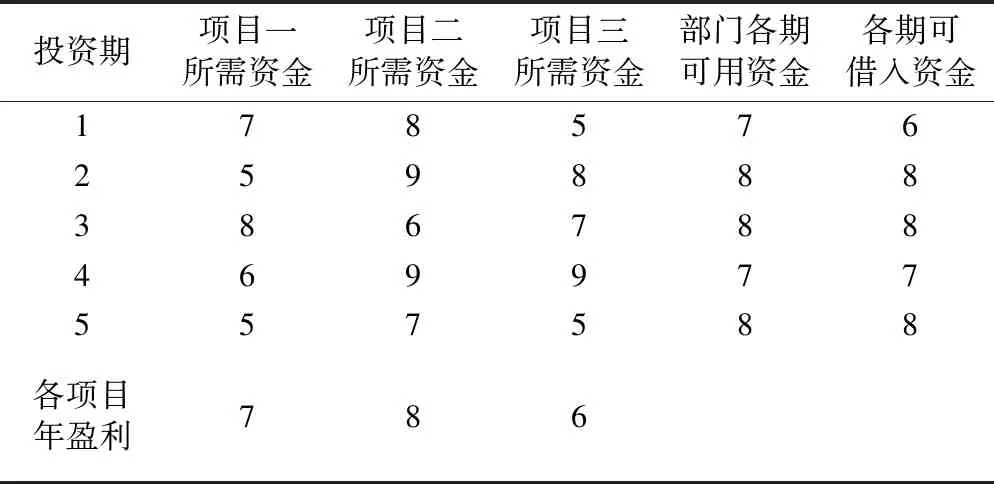
表6 工程投资企业各项目投资参数表 单位：万元

①终值的计算

根据表6以及式(10)可以得到各项目5年盈利的净现值见表7。

表7 项目盈利净终值表 单位：万元

②目标函数及约束方程的的建立

当多余投资资金不可用于下年，根据本例可设投资分配比例分别为x1、x2、x3,将数据带入式(7)，则有如下的线性规划方程：

(13)

将上述线性规划方程整理并化为标准型：

(14)

借助MATLAB软件计算得mbhs=35.5480,x1=0.6667,x2=0.1444,x3=0,也就是对项目一的投资比例为66.67%，对项目二投资比例为14.44%，对项目三不投资。

若当年资金可用于下年投资使用，则有线性规划方程为：

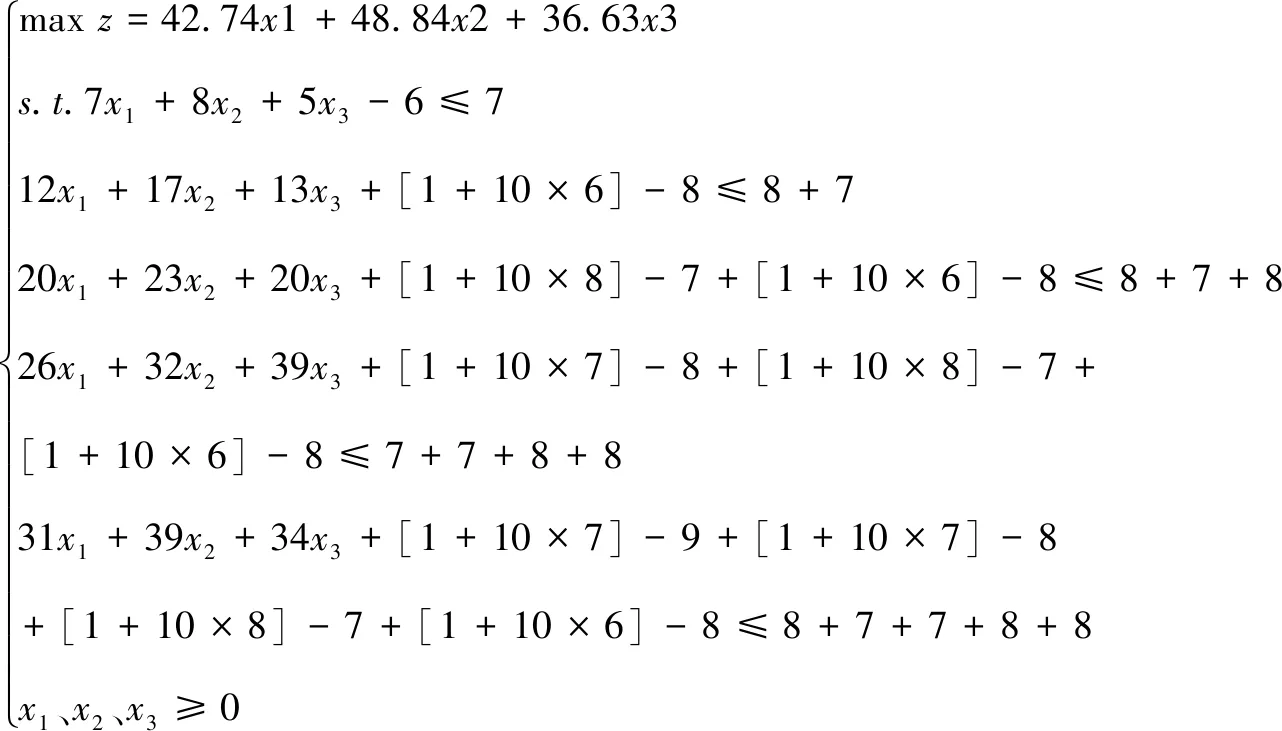
(15)

对上述线性规划方程整理并化为标准型：

(16)

由MATLAB得出最优解mbhsz=57.2058,x1=1.3385,x2=0,x3=0,即对项目一的投资比例为1.3385，对项目二、项目三不投资。

2.3 数据结果分析

2.3.1 完全自由资金投资分配结果对比

由例一可以看到对完全自由资金投资分配的两种结果。当年资金不可留作下年利用时，可获得的盈利最大净现值为27.2165万元；当年资金可以在下年循环利用时，可获得的最大盈利净现值为27.9910万元。显然，可以在下年循环利用资金的状况下，工程投资企业能够获得更大的利润。

在各项目中，项目二的净现值最大，为30.33万元。按照传统的遵循净现值法最大原理，所选择的方案应当为项目二。但是通过建立线性规划方程后得出的结果是对项目二投资0.0732。通过对结果的分析可以发现，如果选择项目二进行投资，第一年投资费用需要8万元，而部门可用资金为7万元，假设7万元全部用于投资，则对项目二的投资份额为87.5%，收益为8×0.875=7万元。按线性规划所得结果，对项目一投资0.7886，对项目二进行投资0.0732，对项目三投资0.1789，则第一年所需费用成本为0.7886×7+0.0732×8+0.1789×5=7.00万元，收益为0.7886×7+0.0732×8+0.1789×6=7.2205>7万元。由此可见，单一的净现值方法对方案的评选是不够全面的。净现值法具有诸多的局限性，如不能反映项目自身的报酬率及投资额有时无法做出正确决策等问题[14]。借助线性规划方程的方法结合净现值法能够更加科学系统的评选方案。

2.3.2 含有借入资金的投资分配结果

当工程投资企业将借入资金也用于投资资金分配时，通过例二可以得知，当项目情况、投资期、基准收益率等条件不变时，借入资金进行投资，每年多余的投资资金未用于下一年时，最大的投资净终值为35.5480万元，将净终值转换为净现值后最大投资净现值为33.8239万元。结果大于只有自有资金时的盈利净现值，可见当工程投资企业投资决策时使用一定的借入资金是有利于工程投资企业把握投资机会，从而实现更好盈利。

当工程投资企业可以将多余的投资资金用于下一年时，投资的净现值为57.2058×0.9519=54.4542万元，远远大于同等情况下未借入资金时的盈利情况，同时也远大于未将资金利用于下年的情况。可见，当工程投资企业借入一定资金用于生产，并且在投资决策时考虑资金的循环使用时，更有利于工程投资企业实现高效率的盈利。

3 结束语

对于非公益性工程投资企业而言，获得盈利是工程投资企业的第一目标。工程投资企业通过各类生产、投资来获得盈利，谋求发展。特别是当投资者处于劣势竞争地位的时候更倾向于关注自己收益的大小[15]。传统的项目往往通过贴现值等经济手段来进行选择，手段单一，并且考虑的影响因素不够全面。本文通过结合线性规划模型方法，对两种资金来源情况下的投资项目分配问题进行数学分析，建立模型并求解。这一方法相比较于传统净现值法而言，解决问题的速度更快，效率更高，同时考虑的因素更加全面。