水泥混凝土路面板底脱空区动水压力特性研究

曾晓辉，刘海川，兰旭丽，朱华胜，李颖洁

(1. 中南大学 土木工程学院，湖南 长沙 410075；2.西南交通大学 土木工程学院，四川 成都 610031)

0 引言

水泥混凝土路面板底脱空是目前较为普遍的道路病害，是影响水泥混凝土路面使用寿命的重要因素之一[1-4]。脱空的出现对水泥混凝土路面的承载是极为不利的，特别是板角、板边部位，在初始脱空的基础上由于降雨等原因，有时脱空区处于饱水状态，在车轮荷载作用下，路面板与基层之间会产生高压水流，从而侵蚀冲刷基层表面。当荷载特别大时，比如超载车辆作用在脱空区上，还会在脱空区尖端产生极大的动水压力，从而产生水力劈裂作用，致使脱空区扩展脱空区进一步增大。当脱空增大到一定尺寸在车辆荷载作用下便会发生局部断裂，从而降低行车舒适度及道路使用寿命。可见水致损害在道路破坏过程中起着极为重要的作用[5-8]。

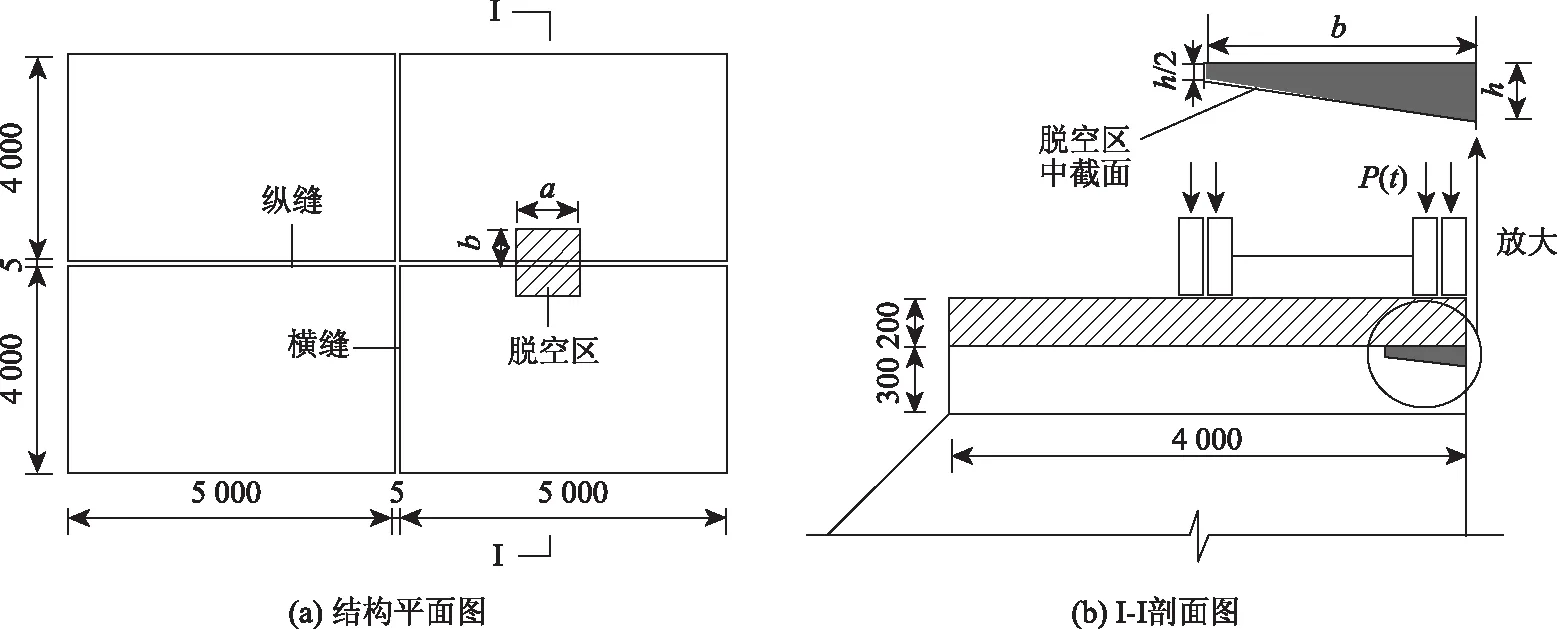
图1 计算模型(单位:mm)Fig.1 Calculation model(unit:mm)注: 图中a,b分别为脱空区的长与宽;h为脱空区开口高度，脱空区尖端厚度取h/2;P(t)为行车荷载。

由于动水压力产生和作用机理的复杂性，目前国内外在水泥混凝土领域对相关问题仅有初步的研究。张铁富等[9]通过数值模拟和断裂力学计算对存在初始脱空区的路面板进行了分析，发现水的劈裂作用使脱空区的尖端应力有大幅度的提高，但考虑的水压力只是估计值。张国雄等[10]进行了水泥混凝土路面板角脱空的试验，发现荷载脱空面积和频率对最大动水压力有一定影响，但其并未研究脱空区内动水压力及速度的分布等特性。文献[11]推导了脱空区内动水压力的分布解析式，但其简化模型过于理想。在重力坝领域也有类似的研究，王克峰等[12]基于扩展有限元法并考虑流固耦合效应，进行了混凝土坝水力劈裂问题的数值模拟研究，发现水压越接近裂尖位置越小，但并未对动水流速进行分析。徐世烺和Brhwiler进行了机械荷载与静水压力耦合水力劈裂试验，发现脱空区内静水压力会降低结构承载能力[13-14]，但其只考虑了静水压力，难以应用于受动水压力的道路结构。

本研究基于材料力学中两端固定梁和悬臂梁的挠度函数，叠加推导了车辆荷载作用下三维状态板底脱空区中截面(图1(b))动水压力分布解析式，同时运用有限元软ANSYS、CFX建立三维有限元双向流固耦合模型，分析了轴重、车速、脱空区尺寸等对脱空区内动水压力及流速的影响，明确动水压力对道路的水致损害机理，为进一步防止道路损伤及损伤修复提供依据。

1 水泥混凝土路面板底脱空区内动水压力计算模型

一般而言，在数值模拟中将水泥混凝土道路简化成3层，即水泥混凝土路面结构(面板层、基层)以及路基，如图1所示。本研究在路面板与基层层间接触区板边中部设置一横截面为梯形的棱柱体做为脱空区，如图1(b)所示。假设脱空区充满水，车辆荷载以双轴双轮组考虑，轮的右边两轮作用于板底脱空区上方。路基底面固定约束，其他面均自由。鉴于实际道路面板的边长通常介于3.0～6.0 m，取路面板尺寸为5.0 m×4.0 m，厚度按照规范取常用厚度0.2 m，为方便建立有限元模型，取基层平面尺寸为5.0 m×4.0 m，厚度为0.3 m，为使数值模拟尽量符合实际情况，取路基厚度为6 m，边坡坡度为1∶1.5[15]。相关计算参数见表1。

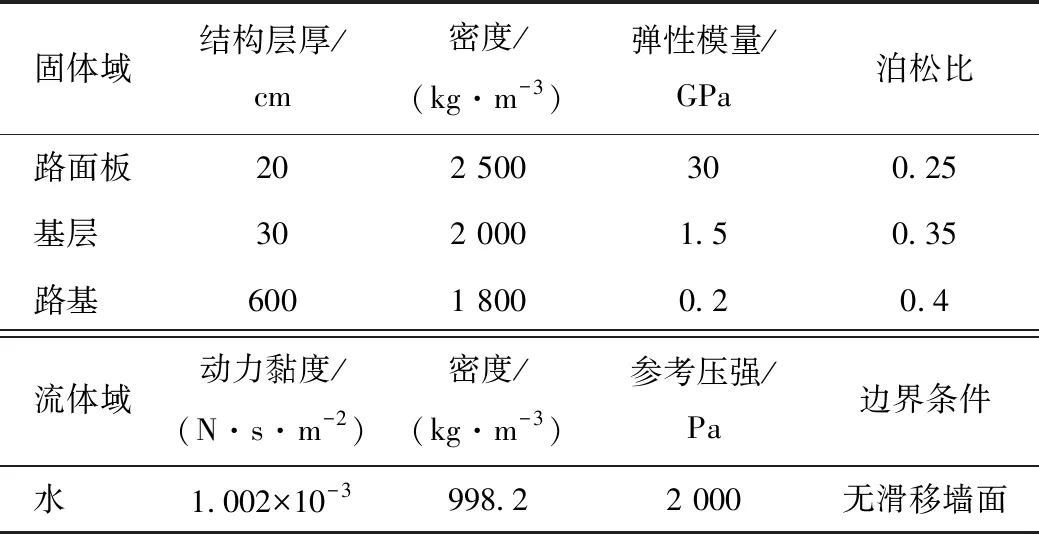
表1 计算参数Tab.1 Calculation parameters

为模拟车辆后轮(双轴双轮组)经过板底脱空区的工况，将行车荷载简化为两个周期的半波荷载[16-18]，对于不同的轴载，分别选取不同的充气压力，并按式(1)计算半波荷载。

(1)

式中，p为汽车静载，大小为轮压值；v为车速；l为轮印长度；qmax为汽车动载最大值,qmax的值一般不超过汽车静载p的0.3倍，取qmax= 0.2p；t为时间。荷载作用面简化成长度为0.24 m的矩形，宽度由轴重和接触压力计算，各组数值列于表2。

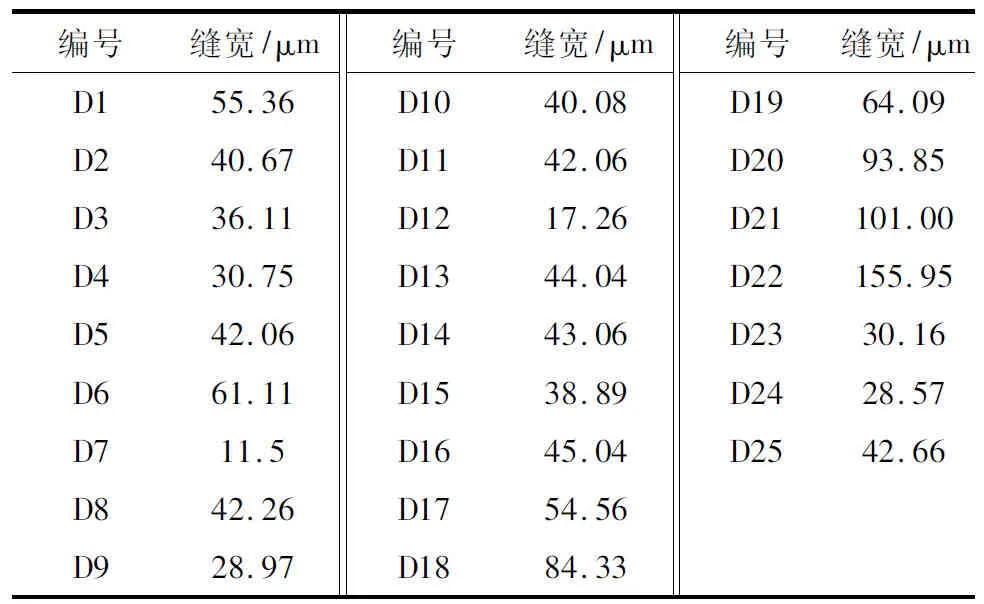
表2 轮胎轴重、充气压力及接触面积值Tab.2 Values of tire axle load, inflation pressure and contact area

2 脱空区水压力分布理论分析

描述空间流体运动的一般方程是Navier-Stokes方程，然而由于流体运动状态及边界条件的复杂性，Navier-Stokes方程难以得到理论解，往往需要简化模型和计算方法来求解[16]。目前较为常用的简化计算方法是控制体积法。由于脱空区内的空间流体运动属于复杂的三维流动问题，为简化计算，提出以下基本假定：(1)脱空区内水是不可压缩流体；(2)水流属于牛顿流体满足摩擦定律；(3)脱空区壁面无渗水；(4)脱空区开口厚度远小于其深度和宽度；(5)忽略流体沿路面纵向方向的流动。基于以上假定，可将三维空间水压力计算简化为图2所示平面问题[11]。

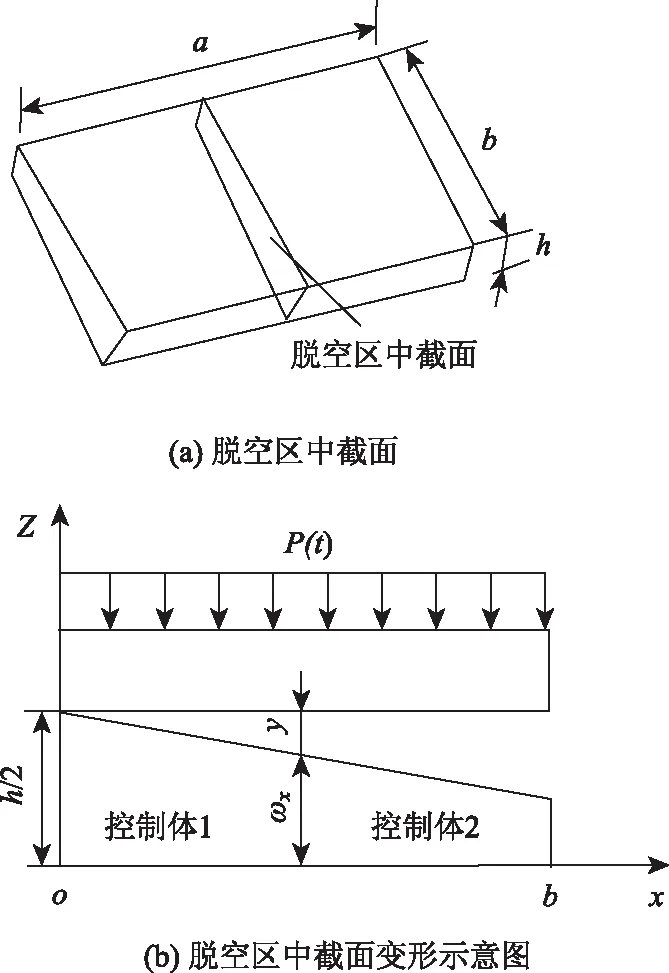
图2 脱空区示意图Fig.2 Schematic diagram of void area注：图中a，b，h，P(t)指代同图1;y和ωx分别为横坐标x处的板位移、脱空区高度。

采用控制体积法求解时，不可压缩流体质量守恒定律可描述为[19]：

(2)

式中，V为控制体体积；Ω为控制体的表面；m为控制体质量；ρ为流体的质量密度；u为速度矢量；n为控制体表面的外法线矢量；A为边界条件。

不可压缩流体动量守恒定律描述为：

(3)

式中，M为控制体积的动量；F为作用在控制体积上的力矢量。

文献[8]根据以上定理推导了图2所示矩形脱空区平面内动水压力分布解析式。

情况 4 设d(v)=6,则f3(v)≤⎣」=3,且ch(v)=6-4=2。由权转移规则知6-点转给3-点、3-面权值,当6-点作为三角形的外邻点时也转给三角形权值。

(4)

(5)

式中，Px为横坐标x处的水压力；b为脱空区宽度；Pb为开口处的静水压力；F为集中车轮荷载；μ为动力黏滞系数；Vx·max为横坐标x处的最大水流速度；ωx为横坐标x处的脱空区高度，ωb为边界b点处的脱空区高度(图2)；其中β(x)为变形系数，其作用类似于弹簧的弹性系数，对于本研究的计算模型，板底脱空区跨中截面ωx可由材料力学中两端固定梁和悬臂梁的挠度函数叠加推出[20]：

(6)

式中，E为混凝土路面板弹性模量；I为路面板脱空区域惯性矩。

联立式(6)与式(4)中ωx=h+Fβx，且F=PtA可得：

(7)

式中，b为脱空区宽度；A为车轮与路面接触面积。

将式(1)、式(7)代入式(4)中，化简可得：

(8)

将式(1)、式(7)代入式(5)中，可得：

(9)

进一步化简可得：

(10)

式(8)、式(9)即为水泥混凝土路面板底脱空区内动水压力及最大水流速度的分布解析式，式(10)为最大水流速度的解析解。由式(8)可知动水压力与轴重大小、车速呈二次方关系；由式(9)可知由于车轮荷载作用下路面板的位移导致脱空区开口量变化是很微小的，即此时变形系数β(x)很小，可知此时最大水流速度Vmax与荷载Pt近似成线性关系，结合式(1)可知Vmax与静载p(即轴重F)成线性关系，与车速v成正相关。

3 有限元模型

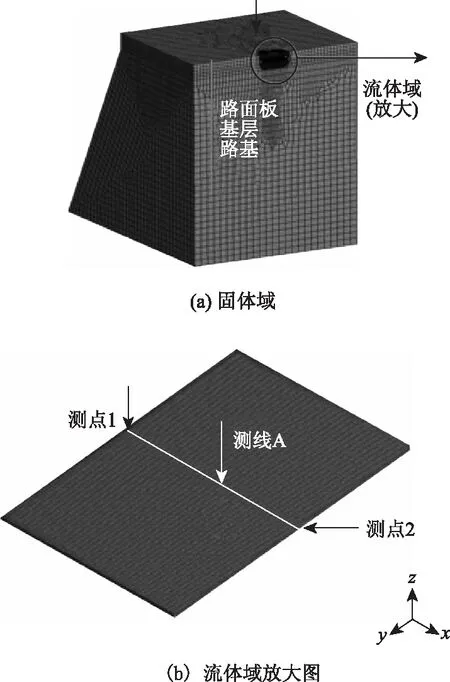
图3 有限元模型Fig.3 Finite element model

4 结果分析

4.1 水压力及流速分布分析

当脱空区平面尺寸为0.6 m×0.4 m，脱空区开口高度为0.004 m时，在轴载100 kN车速60 km/h的车辆荷载作用下水压力与水流速度最大值时刻下，流体域应力速度大小分布云图如图4所示。

图4 峰值时刻水压力与水流速度分布云图Fig.4 Nephograms of water pressure and flow velocity at peak time

由图4可知，水压力及水流速度沿y轴方向变化不大，且水压力最大值位置在脱空区尖端长边中点处，且离尖端越远水压力越小。水流速度最大值位置在脱空区开口边缘长边中点处，离尖端越近水流速度越小。取测线A以及测点1、2来简化分析水压力、水流速度的大小及分布。由于水压力、水流速度随时间不断变化，根据最不利原则选取最大水压力、水流速度出现时刻来研究。为找出最不利时刻，取测点1、2为研究点，轴载100 kN行车速度60 km/h(相应荷载周期为0.009 s)作用下水压力、水流速度最大值随时间的变化如图5所示。

图5 轴重100 kN车速60 km/h时水压力与 水流速度最大值随时间的变化Fig.5 Maximum water pressure and flow velocity varying with time at 100 kN axle load and 60 km/h vehicle speed

从图5可以看出，固定点的水压力及速度随时间成正弦函数变化，最大水压力随时间的变化趋势与最大水流速度随时间变化趋势有一定的相位差。从图中可以看出最大水压力出现时刻在0.002 s，最大水流速度出现时刻在0.003 s。可见最大水压力以及最大水流速度出现时刻均不在荷载作用峰值时刻。

4.2 轴重对水压力、水流速度的影响

当脱空区平面尺寸为0.6 m×0.4 m，开口高度为0.004 m时，在车速为60 km/h(由式(1)知荷载周期0.008 4 s)时，不同轴载(80，100，120，140，160 kN)作用下，板底脱空区内水压力、水流速度分布及峰值随轴重的变化如图6所示。

图6 轴重对水压力及水流速度的影响Fig.6 Influence of axle load on water pressure and flow velocity

由图6(a)、6(b)知，水压力沿脱空区深度方向呈增大趋势，其最大值发生在尖端处，最小值发生在脱空区边缘；水流速度沿脱空区深度方向呈增大趋势，其最大值发生在脱空区边缘，最小值发生在脱空区尖端。这可由能力守恒解释，流速越大的位置动能越大，其势能自然越小，因而水压力越小。由图6(c)知，水压力随轴重增大而增大，且基本成二次方关系，水流速度的峰值与车速呈线性关系，与理论推导基本一致。

4.3 行车速度对水压力、水流速度的影响

车速的变化通过荷载周期的变化来体现，脱空区平面尺寸为0.6 m×0.4 m，开口高度为0.004 m，在轴重100 kN时，不同车速下行车荷载作用下水压力及流速分布如图7所示。

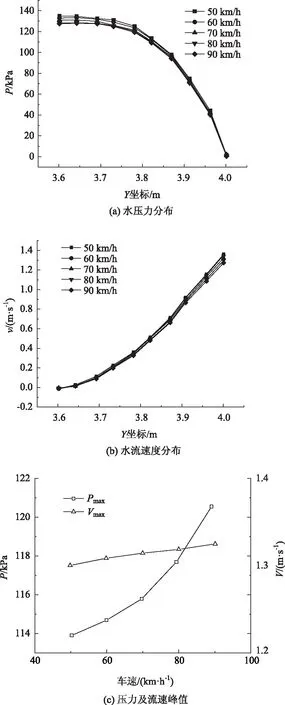
图7 行车速度对水压力及水流速度的影响Fig.7 Influence of vehicle speed on water pressure and flow velocity

从图7(a)和(b)可以看出：压力沿脱空区深度方向呈增大趋势，其最大值发生在尖端处，最小值发生在脱空区边缘；水流速度沿脱空区深度方向呈增大趋势，其最大值发生在脱空区边缘，最小值发生在脱空区尖端。从图7(c)可以看出：水压力峰值与车速呈二次方关系，与理论推导基本一致，水压力随车速变化的增幅大约为每10 km/h增加1 kPa；水流速度峰值随车速增大而增大，但影响较小。

4.4 脱空尺寸对水压力、水流速度的影响

在车速为120 km/h，轴载140 kN，脱空区平面尺寸为0.6 m×0.4 m时，板低脱空区内水压力、水流速度分布及峰值随脱空区开口高度的变化如图8所示。

图8 脱空区开口高度对水压力及水流速度的影响Fig.8 Influence of opening height in void area on water pressure and flow velocity

从图8(c)可以看出压力及流速峰值与脱空区开口高度基本成反比关系，且开口高度大于4 mm后动水压力极剧减小，由此可见动水压力对水泥混凝土路面脱空区的初期扩展有较大促进作用，当脱空区开口高度扩展到一定程度，动水压力对脱空区扩展影响减小。此时脱空区的发展可能是因为水流的冲刷作用。

5 结论

针对半波车辆荷载作用下，水泥混凝土路面板底脱空水力特性问题，通过理论分析与数值模拟结合的方法得出以下结论：

(1)基于材料力学中两端固定梁和悬臂梁的挠度函数，推导了三维状态下混凝土路面板脱空区内中截面动水压力及水流速度的分布解析式；动水压力峰值与轴重大小、车速度呈二次方关系；当变形系数β(x)较小时，最大水流速度与荷载近似呈线性关系，与车速呈正相关，但车速对其影响较小；数值模拟结果与理论推导结果基本一致。

(2)脱空区内动水压力沿脱空深度方向呈增大趋势，其最大值发生在脱空区尖端，最小值发生在脱空区边缘；水流速度沿脱空深度方向呈减小趋势，其最大值发生在脱空区边缘，最小值发生在脱空区尖端。

(3)在车辆荷载作用下，轴重、车速、脱空尺寸均会对脱空区内动水压力造成影响；动水压力对水泥混凝土路面层间脱空区的初期扩展有较大促进作用，当脱空区开口高度扩展到一定程度时(本研究模型为>4 mm)，动水压力对脱空区扩展的影响减小，此时脱空区的继续发展可能是因为水流的冲刷作用。