尾水管涡作用下水轮机转轮叶片动水压力特性

李兆军，王玉江，刘福秀，黄钰钰，毛息军

(1.广西大学 机械工程学院，广西 南宁 530004；2.广西科技大学 广西汽车零部件与整车技术重点实验室，广西 柳州 545006)

0 引言

混流式水轮机弯肘型尾水管在部分负荷工况下会产生尾水涡流，造成转轮叶片动水压力中存在着异常压力脉动[1]。这种异常压力脉动可能使转轮叶片产生强烈振动，进而造成转轮叶片出现疲劳裂纹，严重危害机组的安全运行[2-3]。因而在研究水轮机转轮叶片动力学特性的过程中，有必要研究尾水管涡对转轮叶片动水压力的影响。

目前有关尾水管涡对转轮叶片动水压力的影响研究，主要通过计算流体力学(computational fluid dynamics，CFD)数值模拟和试验测试分析的方法。通过数值模拟方法，钟林涛等[4]研究了转轮出口速度、出口旋流数和涡带形状等因素与尾水管涡带的关系。FOROUTAN等[5]研究了泄水锥射流与尾水管中心的轴向动量以及尾水管涡的死水区的关系。通过试验测试方法，王小龙等[6-7]研究了转轮叶片入口处的压力脉动幅值和频率。以上两种方法研究了不同工况时的动水压力变化规律，没有得到反映动水压力与水力参数和结构参数的数学模型，难以进行转轮叶片动水压力的暂态过程分析[8]。而数学模型能够反映动水压力与水力参数和结构参数的内在关系，可对转轮叶片动水压力的暂态过程进行分析，且暂态过程分析又是研究转轮叶片动力学特性的基础工作，而目前有关此方面的研究鲜见文献报道。

本文以水轮机转轮叶片为研究对象，根据水轮机转轮叶片准三元反设计的特点，应用有限单元法建立水轮机转轮叶片的准三元有限元模型，构建尾水管涡作用下的转轮叶片上动水压力的数学模型，并通过实例分析进行验证。

1 水轮机转轮叶片的准三元有限元模型

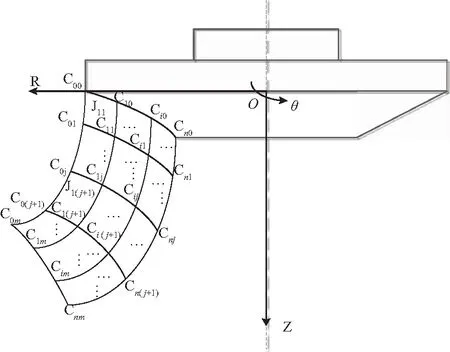
图1 水轮机转轮叶片坐标系Fig.1 Global coordinate system of a turbine runner blade

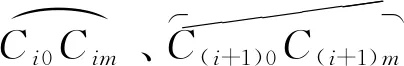
PJij(r,θ,z,t)=N1Pij+N2P(i+1)j+N3P(i+1)(j+1)+N4Pi(j+1)，

(1)

式中：Pij、P(i+1)j、P(i+1)(j+1)、Pi(j+1)为节点Cij、C(i+1)j、C(i+1)(j+1)、Ci(j+1)的尾水管作用下的压力脉动，N1、N2、N3、N4为节点Cij、C(i+1)j、C(i+1)(j+1)、Ci(j+1)动水压力的形函数，根据水轮机转轮叶片准三元理论的动水压力变化规律[9]，尾水管作用下的压力脉动形函数为

(2)

式中：a、b分别为单元长度和宽度的一半。

2 尾水管涡作用下的水轮机转轮叶片动水压力

水轮机机组在部分负荷时，由于水轮机流量的减小，水流在转轮出口产生具有与转轮旋转方向相同的圆周分量，导致在转轮出口的正环量增加。当环量达到一定程度，水流在尾水管产生一个与转轮旋转方向相一致的偏心涡带[4]。尾水管涡引起了转轮叶片的出口回流，在回流作用的影响下，转轮叶片节点Cij的压力脉动pij可表示为[10]

pij=kijAijsin(2πft+φ)，

(3)

式中：Aij为节点Cij所在截面尾水管涡的压力脉动幅值，φ为初相位，与初始时刻的叶片相对位置有关；kij为尾水管涡引起的回流作用下叶片节点Cij的动水压力系数，与节点位置参数有关，为

(4)

式中：ε为叶片翼型常数，且-1≤ε≤1，可根据转轮叶片的具体翼型确定。

式(3)中f为尾水管频率，在部分负荷工况下，尾水管频率是转频和设计水头的函数，可表示为[11]

(5)

式中：n为水轮机转轮的转速，Q为水轮机实际流量，Q0为水轮机额定流量，ra为中央流线出口处半径，β为叶片出口水流角，S为转轮出口过水断面面积，且S=2πdra，d为出水边叶片弧长长度。

根据布拉修斯定理[12]，式(3)中节点Cij所在截面尾水管涡的压力脉动幅值Aij可用尾水管涡带圆周速度分量的动量表示为

(6)

(7)

式中：rw为尾水管入口截面半径;z0为泄水锥的深度;τ1、τ2为待定正常数，可根据试验结果的经验数据确定。

根据文献[14]可知，当Q=0.9Q0，H=H0时，尾水管涡带消失；而在Q=0.25Q0，H=H0部分负荷运行区时，下环处尾水管涡带半径接近于尾水管入口截面半径，依据具体的流量和水头，可计算出τ1、τ2。

式(6)中涡带偏心距e可根据仿真结果和试验数据获得[2]

(8)

(9)

式中:Cv为尾水管涡引起的节点Cij圆周速度与节点Cij绝对速度圆周分量的相关系数，与尾水管涡带运行的工况有关。uij为节点Cij的绝对速度的圆周分量，可表示为

(10)

将式(4)～(10)代入到式(3)中，并整理得节点Cij的尾水管涡作用下转轮叶片的动水压力为

(11)

由式(11)可知，尾水管涡作用下转轮叶片的动水压力幅值随着流量的增加而逐渐减小，随着水头的增加而增加；而尾水管涡作用下转轮叶片的动水压力频率随着转速的增加而逐渐增加，随着水头的增加而减少。

根据式(11)尾水管涡作用下转轮叶片节点Cij的动水压力，可得到尾水管涡作用下的Jij单元另外3个节点C(i+1)j、C(i+1)(j+1)、Ci(j+1)的动水压力，分别表示为

(12)

(13)

(14)

将式(2)、(11)至(14)分别代入式(1)中，即可得到t时刻尾水管涡作用下转轮叶片Jij单元中任意位置(r,θ,z)动水压力，并依据式(3)，可以表示为

(15)

式中：Bij、B(i+1)j、B(i+1)(j+1)和Bi(j+1)分别为尾水管涡作用下水轮机转轮叶片节点Cij、C(i+1)j、C(i+1)(j+1)和Ci(j+1)的动水压力幅值，且

(16)

(17)

(18)

(19)

由式(15)可知，尾水管作用下转轮叶片的瞬时动水压力是一个时间和空间的函数，不仅自身的位置参数有关，如：Z轴坐标、半径等；也与水力参数有关，如：流量、水头、转速等；而且与水轮机结构参数有关，如：泄水锥长度、尾水管入口截面半径、转轮出口过水断面面积、叶片出口水流角等，反映了动水压力与结构参数和水力参数之间的关系，可以通过改变水力参数进行暂态过程分析，这也为进一步研究尾水管涡作用在水轮机转轮叶片上的动力学特性提供理论依据。

3 实例分析

3.1 实例

根据目前的研究成果，尾水管涡作用下的转轮叶片动水压力与运行工况相关。动水压力频率是转频和设计水头的函数；部分负荷运行区，涡带偏心严重，形成圆柱螺旋涡，压力脉动幅值大；而在额定负荷附近时，涡带不明显甚至消失，压力脉动很小[16]。本文选取Francis-99混流式水轮机转轮叶片为研究对象，验证数学模型的可行性，并对尾水管涡作用下的转轮叶片动水压力暂态过程变化规律进行研究。

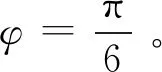
根据准三元反设计的特点，采用5条径向线与9条轴向线将叶片分成45个单元，其中第1条径向线为上冠处，第5条径向线为下环处，则长叶片上的各个节点如图2所示。进水边的节点为C00,C01,…,C04；出水边的节点为C80,C81,…,C84。

图2 试验研究对象结构示意图Fig.2 A structural sketch of the runner blade

3.2 数学模型验证

根据式(7)可知，尾水管涡初始于泄水锥的尾部，故以超过泄水锥深度的节点C71为研究对象。通过式(11)计算出节点C71的动水压力，其动水压力值时域仿真曲线与文献[17]的试验数据，如图3所示。

由于测试的试验数据中压力不仅包含了尾水管涡作用下的压力脉动，也包含了其他压力脉动，所以部分数据误差比较大，由图3可知，节点C71处的平均误差为2.84 %。最大误差值为8.32 %，从数据对比中，可以证明公式(11)在计算节点动水压力的有效性，进而说明了数学模型的可行性。

通过式(15)即可得到任意位置处的动水压力，其中t=0.08 s时叶片任意位置的动水压力如图4所示。从图4中可以看出，瞬时的动水压力沿轴线方向逐渐减少，瞬时的动水压力沿流线方向也逐渐减少。与文献[17]的尾水管涡作用下转轮叶片动水压力CFD仿真图相比较，瞬时时刻的最大误差出现在叶片的出水边近下环处，误差为7.92 %。从数据对比中，可以证明公式(15)在计算任何位置动水压力的有效性，这也证明数学模型的有效性。

图3 节点C71的试验值与仿真值Fig.3 Time domain simulation curves and the experimental data of node C71

图4 尾水管涡作用下t=0.08 s时转轮叶片动水压力分布图Fig.4 Hydrodynamic pressure diagram of the runner blade at t=0.08 sunder the vortex rope in draft tube

3.3 动水压力暂态过程变化规律

为了研究尾水管涡作用下转轮叶片的动力学特性，对暂态过程中动水压力变化规律进行研究。通过改变水轮机运行工况，研究水力参数对尾水管涡作用下转轮叶片节点C71的动水压力幅值的影响。

图5为额定转速和额定水头时，不同流量下尾水管涡作用下转轮叶片节点C71的动水压力幅值仿真曲线，从图5中可以看出，当转速和水头不变时，随着流量的增加，尾水管涡作用下的转轮叶片动水压力幅值逐渐减小；当运行工况高于额定功率的90.1 %时，尾水管涡带的半径接近于零，转轮叶片动水压力幅值也接近于零，此时可忽略动水压力对转轮叶片的影响。而在高负荷下，又重新出现圆柱形死水区，此时尾水管涡作用下转轮叶片动水压力幅值小于6 Pa，也可以忽略不计。

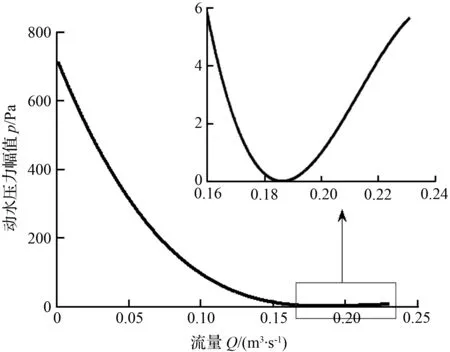
图5 不同流量下尾水管涡作用下的节点C71的动水压力幅值仿真曲线Fig.5 Simulation curve of the hydrodynamic pressure amplitude of node C71 for different discharge

图6为额定转速和额定流量时，不同水头下尾水管涡作用下的转轮叶片节点C71动水压力幅值仿真曲线。从图6中可以看出，当转速和流量不变时，随着水头的增加，尾水管涡作用下的转轮叶片的动水压力逐渐增加。当运行工况低于额定功率的26.4 %时，死水区几乎充满整个尾水管，动水压力幅值接近零，此时可忽略动水压力对转轮叶片的影响。结合图5和图6可知，尾水管涡作用下转轮叶片的动水压力主要产生在额定功率的26.4 %～90.1 %的运行工况。

图6 不同水头下尾水管涡作用下的节点C71的动水压力幅值仿真曲线Fig.6 Simulation curve of the hydrodynamic pressure amplitude of node C71 for different water heads

以上研究表明，应用本文所建立的尾水管涡作用下的转轮叶片动水压力数学模型，对Francis-99混流式水轮机转轮叶片进行实例分析，验证了数学模型的可行性，并研究了尾水管涡作用下的水轮机转轮叶片的动水压力暂态过程变化规律。

4 结论

根据水轮机转轮叶片准三元反设计的特点，应用有限单元法建立了尾水管涡作用下的水轮机转轮叶片的动水压力数学模型，揭示了尾水管涡作用下水轮机转轮叶片的动水压力暂态过程变化规律，研究表明：

① 在暂态过程变化中，尾水管涡作用下的转轮叶片动水压力主要产生在额定功率26.4 %～90.1 %的运行工况；当运行工况低于额定功率的26.4 %时，死水区几乎充满整个尾水管，动水压力幅值接近于零；当运行工况高于额定功率的90.1 %时，尾水管涡带的半径接近于零，动水压力幅值小于6 Pa。

② 尾水管涡初始于泄水锥的尾部，尾水管涡作用下转轮叶片动水压力自上冠处到下环处逐渐增大，且动水压力最大值出现在转轮叶片下环处靠近出水边的位置。

③ 通过改变数学模型中的转轮叶片位置参数以及水头、流量等水力参数，揭示了转轮叶片复杂的动水压力进行暂态过程变化机理，为进一步研究尾水管涡作用下水轮机转轮叶片的动力学特性提供理论依据。