数学核心素养导向下的高考复习—-2019年高考全国Ⅰ卷文科数学第19题阅卷有感

广东省深圳市深圳科学高中

1 问题提出

笔者有幸参加了2019年高考广东省数学文科19题的阅卷工作,笔者发现学生有众多解法,也有很多出乎意料的错误,在阅卷之余,笔者思考:面对高三数学的复习,教师该如何“复习”? 由此,笔者对学生的答题情况进行了分析,并把学生所犯的错误进行了归纳,为教学工作提供借鉴与帮助.

2 试题赏析

题目(2019年高考全国Ⅰ卷文科数学第19题)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.

(1)证明:MN//平面C1DE;

(2)求点C到平面C1DE的距离.

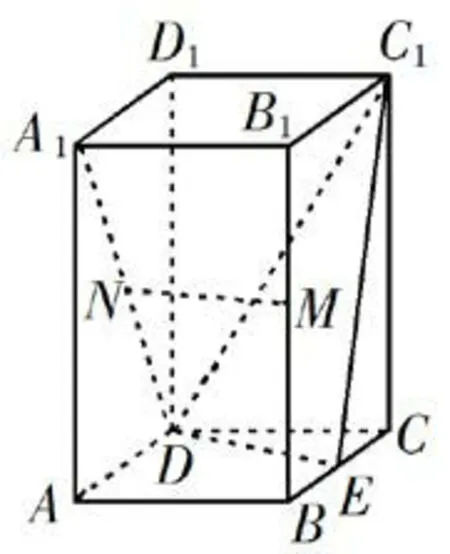
图1

本题考查了直线与平面平行以及点到面的距离问题,以常见的直四棱柱为模型,背景非常熟悉,而且设问方式常规,与平时的模拟卷吻合,属于意料之中的题型.命题者希望通过这种类型的问题来考查考生的几何空间感以及逻辑推理、直观想象、数学运算等数学学科核心素养.总的来看,该题彰显学科特色,有效创新,注重核心素养的考查.不过,从阅卷的实际情况看,学生的作答情况并不理想.

3 考生答题情况

3.1 第(1)小题答题情况

试题的第(1)小问主要是检测线面平行的判定定理知识,考查学生的几何空间感以及逻辑推理能力,学生主要的解法都是通过线线平行的传递性得到MN//ED,具体的有以下两种解法:

方法1连结B1C,ME.因为M,E分别为BB1,BC的中点,所以ME//B1C,且ME=B1C.由题设知A1B1//=DC,所以,四 边 形A1B1CD为平行四边形,可得B1C//=A1D,又因为N为A1D的中点,所以ND=A1D.故ME=//ND,因此四边形MNDE为平行四边形,所以MN//ED.又MN ̸⊂平面C1DE,所以MN//平面C1DE.

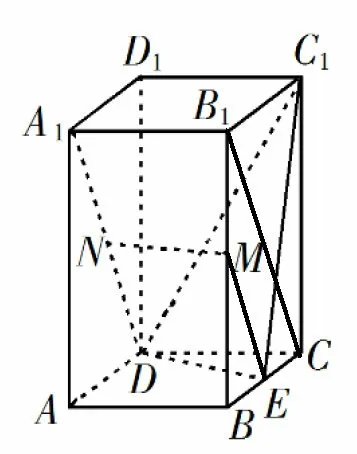
图2

从学生答题情况看,学生选择这种方法的人数较多,大部分学生都能想到利用四边形MNDE为平行四边形得到MN//ED,再利用线面平行的判定定理解决问题;学生出现的主要困难是不知道如何利用已知的中点添加相应的平行辅助线来证明ME//=ND,此处出现了比较典型的错误如下:

(1)由面面平行直接得到结论.如:“在直四棱锥中,因平面A1D1DA//平面B1C1CB,所以ME//=ND,因此四边形MNDE为平行四边形”,这种错误是典型的对面面平行的性质定理使用的条件不熟悉所导致;

(2)跳步严重.例如:“因为E、M、N分别为BC、BB1、A1D的中点,所以ME//ND,又因为因此四边形MNDE为平行四边形”;再如:“连结B1C,ME,在直四棱柱中,平面A1D1DA// 平面B1C1CB,因为平面NDEM分别交两个平面于ND和ME,所以ME//ND”.

这两种“错误”可以认为是超出一般高中生知识水平的一种严重的跳步,学生并没有借助平行的传递性求证线线平行,未证明N,D,E,M在同一个平面上,整个推理过程不严谨,这也说明很多考生分不清主要步骤和次要步骤,一些必不可少的步骤是不能省略的,导致该写的得分点没有写上,得不到相应的分数.

方法2取AD的中点F点,连接NF,FB.因为N,F分别为A1D,AD的中点,所以NF=//A1A,因为M为BB的中点,所以BM=B1B.由题设知AA1=//BB1,所以,NF//=BM,因此四边形BFNM为平行四边形,所以MN//=BF,又因为DF//=BE,所以四边形DEBF为平行四边形,所以BF//=DE,所以MN//ED,又MN ̸⊂平面C1DE,所以MN//平面C1DE.

从学生答题情况看,大部分学生在正确做出辅助线的情况下都能做正确,但是也出现部分同学有严重的步骤缺失,具体来看,学生想利用平行的传递性由MN//BF,BF//DE得到MN//DE,但是学生在得MN//BF时出现了跳步现象,如:“因为M,N,F分别为BB1,A1D,AD的中点,所以MN//BF”,学生并没有借助平行的传递性求证线线平行来证明MNFB为平行四边形,导致考生得不到相应的分数.

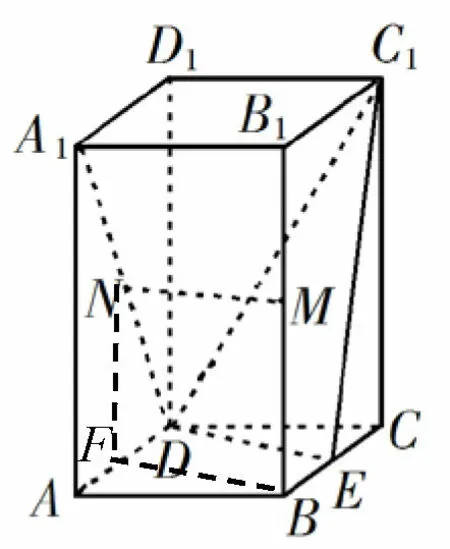
图3

3.2 第(2)小题答题情况

试题的第(2)小问主要是检测点到面的距离,考察学生的直观想象能力和数学运算能力,学生主要有两种思路,解法一是通过等体积法求高,得到点到面的距离,解法二是先过C点作平面的高,再去求高从而得到点到面的距离,具体的解法如下:

方法1(等体积法)点C到平面C1DE的距离为h,根据题意有VC1-CDE=VC-C1DE,即VC1-CDE=h.在菱形ABCD中,E为BC中点,所以DE ⊥ BC,根据题意有所以因为C1C ⊥平面CDE,所以VC1-CDE=

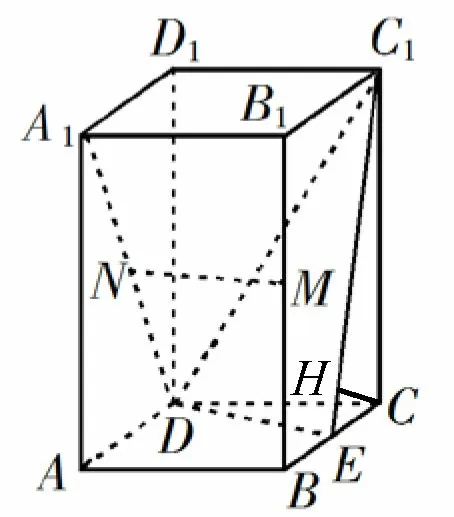
图4

由VC1-CDE=VC-C1DE得到解得点C到平面C1DE的距离为

等体积法是考生最喜欢用的一种方法,因为找不到线面垂直,就找不到垂足,所以等体积法就是解决点到面的距离最佳方法,从阅卷来看,采用等体积法的考生基本上都是正确的占但是也会有考生会出现一些“低级”错误,如考生计算棱锥的体积公式时缺失,典型的计算错误:这样的错误会导致最后失去很多的分数.

方法2(作高法)过C作C1E的垂线,垂足为H.即CH ⊥C1E.由已知可得C1C ⊥平面ABCD,DE ⊂平面ABCD,DE ⊥C1C,因为DE ⊥BC,BC ∩CC1=C,所以DE ⊥平面BCC1B1,因为CH ⊂平面BCC1B1,DE ⊥CH.又因为DE ∩C1E=E,从而CH ⊥平面C1DE,故CH的长即为C到平面C1DE的距离,由已知可得CE=1,C1C=4,所以由等面积法知,从而点C到平面C1DE的距离为

相对于等体积法,考生选择使用这种方法的比较少,这种方法的难点在于寻找线面垂直,考生如果找到CH这条线,最终都得到能正确的计算结果;该题主要的失分点在于学生对于线面垂直的判定定理不熟悉,不能严谨的推证出直线CH垂直于平面C1DE;此外,有部分学生没有能正确的寻找到经过C点且垂直于平面C1DE的直线,有考生误将CE看作点C到平面C1DE的距离.

笔者在阅卷过程中还发现:逻辑思维比较清晰的考生,其试题解答中的推理过程写得也很简洁,关键步骤都写在答卷上,易于分辨.反之,逻辑思维混乱的考生,其试题解答中的推理过程混乱,虽然写得密密麻麻,但却不知所云,答题不在点上,导致失分.甚至,有部分考生已经答题了,而且很多关键点也列出了,但是又涂掉了,从而没有得分,令人惋惜,也有极少数的学生选择使用了向量的方法解决问题,由于使用这种方法的考生人数极少,本文不再赘述.

4 教学与备考建议

高考中的数学学科考试是以数学基础知识为思维材料和操作对象,考查学生各方面已经得到发展的数学核心素养.在高考复习中,教师可以以数学学科核心素养为导向进行高效复习.

4.1 回归教材,夯实基础数学基础知识是数学核心素养的外显表现,是发展数学核心素养的有效载体,基础知识的考核是高考的主要内容和核心知识,从历年的高考真题来看,高考的试题源于教材而高于教材,如第19题只是在教材习题上稍作变形的比较常见的立体几何问题,是考查了立体几何中非常基础而核心的线面平行和点到面的距离问题,但是从考生的答题情况来看,学生对教材上的基础知识掌握不牢,不能灵活运用.因此,平时在教与学的过程中,要回归教材,重视基本知识的形成过程和发展过程的学习,重视定义的理解、公式变形使用、定理的推导,善于挖掘教材例题、习题的价值等; 此外,对于数学学习来说,做题是至关重要的,通过做题才能对知识点加深理解灵活运用,让数学的记忆通向理解从而形成直觉,做题时快速的运算速度能够保证高效思维,解题时的演绎推理能够保证逻辑的准确,还可以通过变式练习来不断提升演练水准.

4.2 注重数学思想方法的灵活运用通过对具体数学思想方法的应用能有效检测数学核心素养的本质属性,在数学思想方法的灵活与综合应用过程中,能够检测知识的迁移、组合、融合的程度,甄别考生核心素养的发展水平和个体差异,实现高考的区分和选拔功能.因此,在高考复习中的解题教学不仅要突出目标意识,强化通性通法,淡化特殊技巧,掌握常用到的方法和基本的招式,学会基本的解题套路;更重要的是注意培养学生的创造性的思维品质,增强交互性,充分调动学生的积极性,注重和展示解题方法的探源、调整、形成过程,教师沿着学生思维轨迹因势利导,克服盲目性,提高自觉性,进行适度引申和变式练习,结合具体问题不失时机地突出数学思想方法,并逐步内化为学生的能力.

4.3 建立核心素养的整体意识高中阶段的数学核心素养包括六个要素,从历年的高考真题来看,高考试题不是孤立的强调考查某一种素养.如全国Ⅰ卷文科第19题,首先考查对立体图形的读图、识图能力,即直观想象的素养,随后的证明过程考查逻辑推理的素养,最后的计算过程考查数学运算的素养.在考查逻辑思维时,要经常与运算结合考查,通过具体的计算推导或证明问题的结论.同时在计算中要较多地糅合逻辑推理的成分,边推理边计算,考生解决问题的过程是综合运用各种素养的过程.因此,高考复习中要注重建立核心素养的整体意识,这就要求教师理解概念,掌握数学的本质,认真研究大型考试试题、高考真题,分析试题时不要就题论题,要注意高考试题与教材中的例题、习题的联系,并且要对高考试题进行适度引申和变式练习,选取能体现事物之间联系、发展变化等观点的素材,科学的创设问题情境,让学生综合所有的科学、技术、工程以及数学内容,并在多种知识间建立联系,解决问题.在试题和习题的选取过程中,要选取材料的呈现方式应该是多种多样、不同复杂程度和结构差异、综合应用各种知识和方法的试题和习题.