单机无源定位飞行方法仿真研究*

吕日毅，李 超，张 阳

(1 92728部队，上海 200040； 2 南京科瑞达电子装备有限责任公司，南京 211100)

0 引言

以F-22和F-35为代表的机载电子战系统(AN/ALR-94)一定程度上颠覆了对传统电子战系统的认识，曾经被认为是防御性，作为有源探测有效补充的电子战无源系统，现在成了探测、跟踪甚至攻击目标的关键设备[1]。如果敌方雷达开机，AN/ALR-94 就能够提供导弹攻击所需的全部信息，引导实施攻击。当无源探测技术水平突破瓶颈，定位精度与时效性满足应用要求，凭借其在军事领域上的诸多优势，将在许多方面与有源定位同等重要，直接作为定位的主要手段[2]。多个国家[3]对于不同体制、不同平台、不同应用的无源定位系统开展了大量研究，包括 LR-100告警监视系统、PRSS无源测距系统、PLAID精确定位与识别系统、LT-500无源瞄准系统、卡尔秋塔无源定位系统、TAMANA无源定位系统、VERA-E无源定位系统、EL-L8300G无源探测系统、CRADA 联合研究开发项目等，美国最新提出的网络化无源定位技术[4]，通过网络内的无源定位设备互联互通实现高精度无源定位解算。

采用测向方法的机载[5]单站[6-8]无源定位方法机动能力强、战术灵活、隐蔽性好[9]，军事应用前景广阔，是研究成果较多的无源定位技术[10-11]。文中针对基于三角交叉原理测向定位的机载单机无源定位飞行方法展开研究，重点剖析影响定位精度[12]的各种因素，最终总结能够提高精度的定位飞行方法。

1 定位误差分析

图1为三角无源定位原理。定位点1(x1，y1)、定位点2(x2，y2)与目标(x，y)连线的夹角为定位张角γ；定位点1至定位点2的连线为定位基线L；定位基线中点上的垂直线为定位基线法线，目标与定位基线中点的连线和基线法线的夹角为法线倾角α；目标与定位基线中点连线的长度为距离R；θ1、θ2为定位三角形的内角。

当测向设备存在误差，定位直线将转化为定位扇形，两定位扇形的交叉区域为目标可能分布区域，按照概率分布，定义目标99%概率落入的圆形区域或椭圆区域为目标分布区，圆的半径d，椭圆的长短轴作为衡量目标定位误差大小的指标。

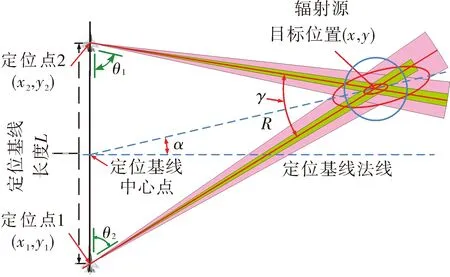
图1 三角无源定位原理

按照三角定位公式，计算目标坐标，推导定位误差如式(1)、式(2)，σθ为设备测向精度。

(1)

(2)

则目标定位误差σs为：

(3)

2 影响定位精度的关键因素分析

2.1 基线长度、目标距离一定，定位张角与法线倾角变化

当定位目标距离、基线长度一定时，定位张角与法线倾角成反比变化，共同影响定位精度，如图2。

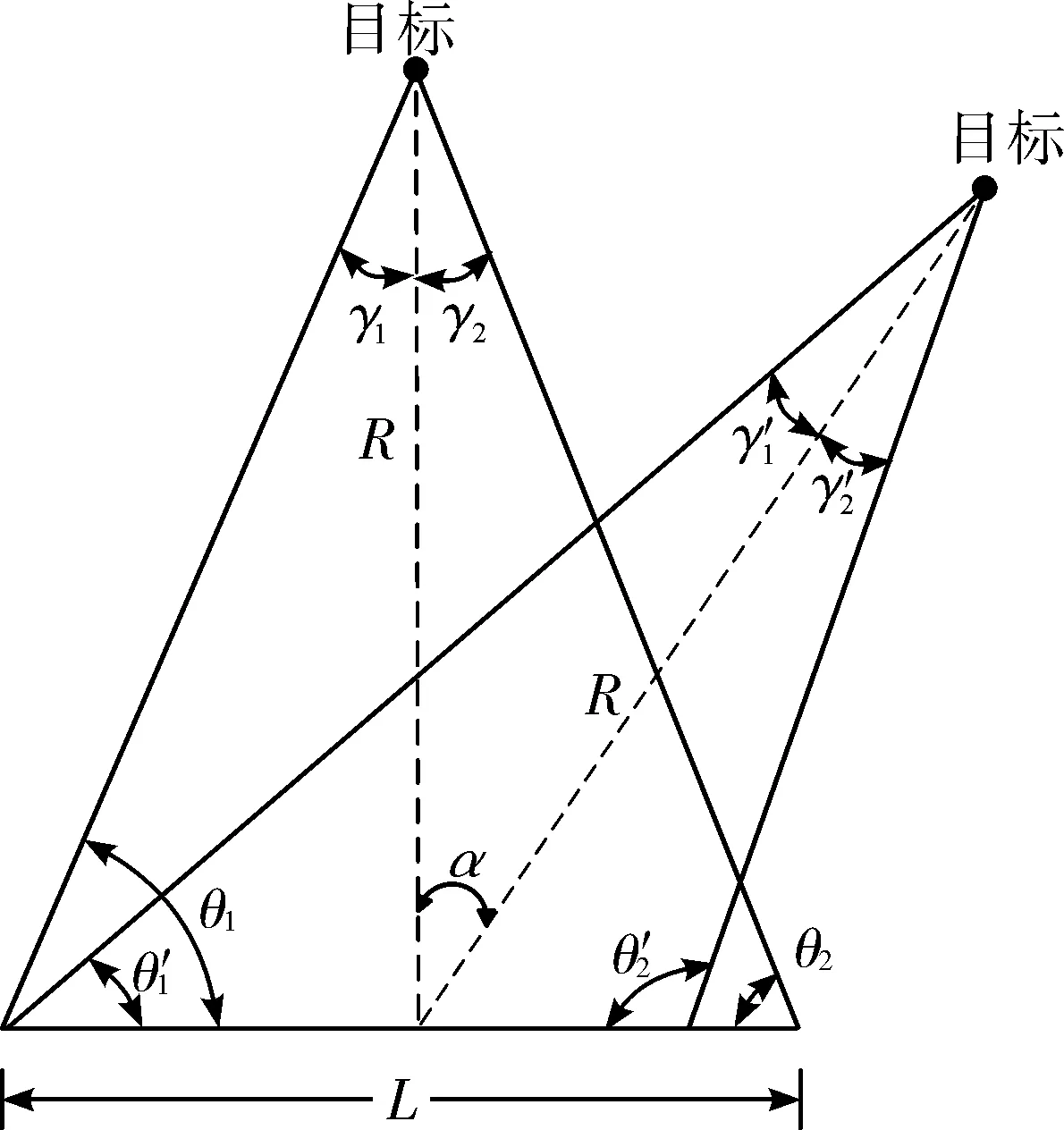
图2 法线倾角对定位态势的影响

求解式(1)、式(2)可得定位误差与法线倾角成反比，倾角越大误差区域越大，定位精度越低。建立仿真模型，参考目前国外相关设备性能指标设定目标距离300 km、定位基线100 km，测向误差2°，定位误差区概率99%，定位误差区域随法线倾角变化如图3，定位误差与法线倾角变化关系如图4。

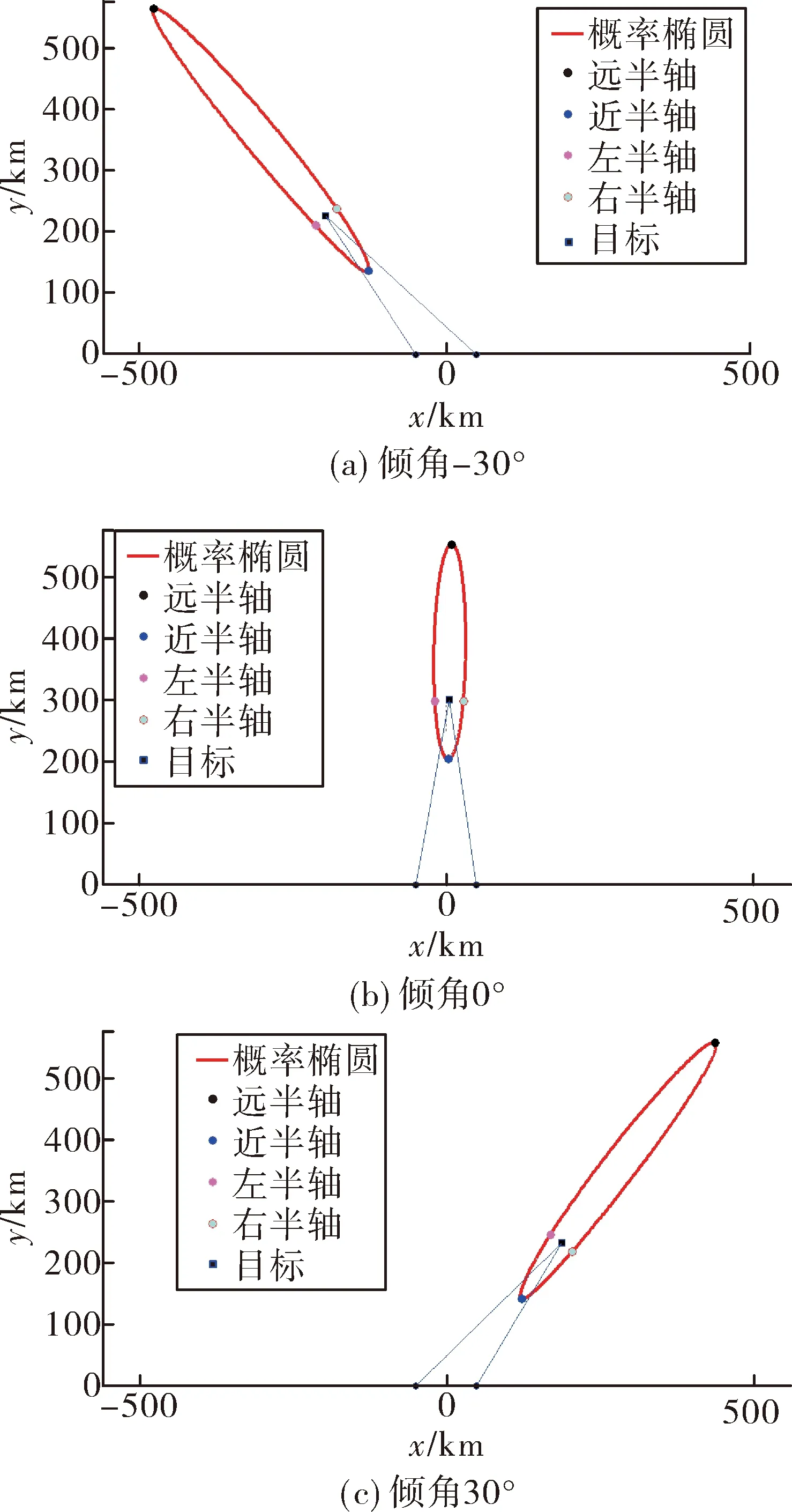
图3 法线倾角对99%概率定位误差区的影响

图4 法线倾角对定位误差的倾向

由以上分析可知，倾角为0°时，定位误差最小。所以在单机定位时应尽量使定位点1与定位点2相对于目标对称，使法线倾角为0°，即目标处于定位基线法线上，从而提高定位精度。

2.2 目标距离、法线倾角一定，定位张角与基线长度变化

如图5，当目标距离R一定、法线倾角α为0°时，定位张角γ与基线长度L成正比，共同影响定位精度。

同样求解式(1)、式(2)，定位误差与定位张角、基线长度成反比，基线越长、张角越大，误差越小。设定目标距离300 km、定位基线100 km，测向误差2°，法线倾角0°，定位误差区概率99%，定位误差区域随张角及基线长度变化如图6。定位误差与基线长度、定位张角变化关系仿真如图7。

图6 基线长度对定位误差区域的影响

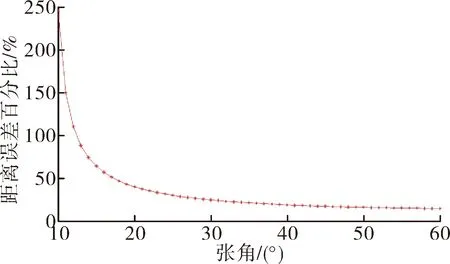
图7 基线长度对定位误差的影响

由以上分析可知，在进行单机无源定位时，在允许条件下应尽量采用长基线、大张角态势，即飞机的定位飞行时间越长，两定位点距离越大，定位精度越高。

2.3 基线长度、法线倾角一定，目标距离与定位张角变化

求解定位公式，可得定位误差σs与定位内角θ成正比，从而与定位距离成正比。即距离越远，定位内角越大，定位张角越小，定位误差越大。进行仿真分析，设定双机间距100 km，测向误差2°，法线倾角0°，定位误差区概率99%，定位误差区域随张角及目标距离变化如图8。定位误差与目标距离变化关系仿真如图9。

图8 定位距离对定位误差区域的影响

由以上分析可知，定位基线应在允许的条件下尽量靠近目标，以提高定位精度。

3 单机定位飞行方法

通过以上影响定位精度的因素分析可得结论：目标与飞机飞行定位基线的相对位置决定了其定位精度。由2.1节可知，当目标距离一定时，倾角越大，定位精度越低，即图10中A点的精度高于E、F点。由2.3节可知，倾角一定时，目标越远，定位精度越低，即C点的精度高于A点，A点精度高于B点。同时由2.2节可知，在飞机能力允许的情况下，飞行时间越长，测距基线越长，定位精度越高。

单机无源定位时可采用图11所示飞行航向。当飞机在定位点1处发现目标时，沿原方向继续飞行0.5～1 min(具体时间由设备性能决定，初定位阶段误差应不大于10%)，开始初定位阶段。初级定位完毕后，由飞行员自行判断精确定位可持续的最长时间T，从而计算出飞行距离d，此时按照初定位阶段目标概率位置及目标距离R，计算由d与R构成的等腰三角形内角θ，此时飞机转向，进入目标精确定位态势，实现精确定位。

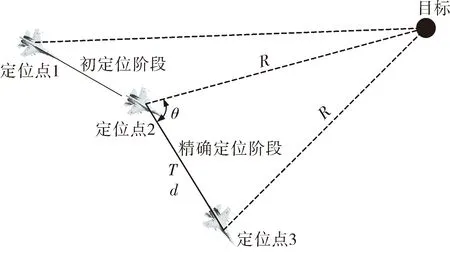
图11 单机精确定位方式

4 结论

从三角定位原理出发，分析法线倾角、定位张角、目标距离、基线长度对定位误差的影响，并验证分析结果，提出了单机无源定位飞行方法，能够对高精度无源定位的应用起到一定促进作用。