对频率捷变信号成像效果影响因素分析*

王永海，刘 朋，周志增，沈 健，郝露华

(中国洛阳电子装备试验中心，河南孟州 454750)

0 引言

传统的ISAR雷达成像，为了获得较高距离分辨率，其信号带宽往往很大，如超宽带直采、传统脉冲压缩去斜等处理方式，均是通过增大信号带宽获得距离高分辨率。而对于窄带雷达而言，由于信号带宽限制，实现高分辨雷达成像则比较困难。当前对于利用窄带雷达成像，也有一些研究成果，如在“脉间变频实现高分辨力成像”、“综合高距离分辨力——频率捷变雷达信号波形的新应用”等文章中，均提出利用频率捷变信号提高距离分辨率的方法[1]。

大多数现代窄带雷达具有频率捷变信号，这种信号常用来抗电子干扰，因为其可在极短时间内覆盖较宽载频范围，有一定概率跳开干扰范围。正是基于频率捷变信号“短时覆盖较宽载频范围”的特点，将频率捷变信号等效为大带宽的线性调频信号，在回波处理过程中进行积累处理和速度补偿，便可以在径向距离上实现一维距离像，提高距离分辨率[2]。

1 基于RD算法的频率捷变信号成像处理方法实现

根据步进频ISAR成像方法[3]，频率捷变成像处理步骤分为提取回波数据、频点重排、运动补偿、距离像合成、包络对齐、相位补偿以及二维成像，其处理流程如图1所示。雷达辐射信号时，选取N个脉冲为一帧数据，且N个脉冲采取频率捷变方式，并覆盖一定频带范围。进行信号接收并获取回波数据后，因各脉冲的频点是随机产生的，为了后续运动补偿，需要先对各帧数据的脉冲频点进行顺序排列，再进行后续处理。其中，目标抽取是合成距离像的重点，常用的目标抽取方法包括：舍弃法、最强散射点法以及基于散射点位置标定法等。

图1 频率捷变信号ISAR成像信号处理流程

对于常规运动目标进行二维成像前往往还需要运动补偿，根据补偿精度的不同，补偿过程一般分为距离对准和相位补偿两步。距离对准将相邻回波信号在距离向对齐，并把目标距离走动造成的多普勒相位变化补偿掉。当前距离对准算法主要包括三类[4]：第一类是最早提出来的散射重心法；第二类主要利用一维距离像之间的相关性进行对齐，称为相关对齐法；第三类是基于图像准则的对齐方法，主要包括最小熵法和最大峰度法。

对于相位补偿，理论上可以使用距离对准得到的距离偏移量的估计值进行相位补偿，但是要达到所需的相位补偿精度，距离估计精度应达到十分之一雷达波长的量级。而实际的距离对准精度与波长相比差距很大，无法用距离偏移量的估计值实现相位补偿，因此必须采用其它方法对平动相位分量进行估计和补偿。基于散射点相位补偿方法的主要思想是从单个散射点或多个散射点的综合，或等效的目标重心中获取平动相位信息，主要包括单特显点法、多特显点综合法、多普勒中心跟踪法等[4]。

2 影响频率捷变信号成像效果原因分析

2.1 目标运动对成像效果影响分析

假设目标以速度V相对雷达运动，则第i个脉冲的复采样信号相位为：

(1)

式中：Tr为脉冲重复周期；Tp为子脉冲宽度；s(i)为频率跳变的随机数列，覆盖所有频点。

按照发射频率递增的顺序重排后的相位关系为：

(2)

式中：r(k)为s(i)重排后产生的数列，k=0,1,…,N-1。可以看出，式(2)中第一项是与距离有关的线性相位项，是产生合成距离像必需的；第二项是目标速度产生的随机相位项，大小和雷达信号重周长度和数量有关；第三项是目标速度和回波延时乘积产生的线性相位项，值较小，可以忽略。

由于频率捷变信号是一种多普勒敏感信号，在实际应用中必须考虑目标的多普勒效应，目标运动会给回波造成附加的一次相位相和二次相位项。由式(2)可知，因速度引起的一次相位项为[5-6]：

φ1=2πiΔf(2V/c)Tr

(3)

一次相位变化是由载频中基频分量f0产生的多普勒频移在不同周期之间形成的相位变化，它是单一谱线，产生距离(时延)误差为：

Δτ=(f0/Δf)·Tr·2V/c

(4)

这一误差与速度V成正比，通常要求距离(时延)误差小于半个合成后的距离单元，即

|Δτ|≤1/(2NΔf)

(5)

代入式(4)有：

|ΔV1|≤c/(4Nf0Tr)

(6)

由速度引起的二次相位项为：

φ2=2πΔf(2V/c)i2Tr

(7)

如果要求最大二次相位项不超过π/2，由式(7)可得：

|ΔV2|≤c/(8ΔfN2Tr)

(8)

因此，在频率捷变信号成像中，一次相位项会在IFFT(傅立叶逆变换)结果中产生耦合时移，但不改变回波形状，该误差与V成正比；二次相位项主要导致IFFT结果能量的发散，其程度也与V成正比。实际应用中，可通过选取较小的N(子脉冲数)和较大的PRF(脉冲重复频率)提高频率捷变信号的多普勒容限，同时采取速度补偿，以降低一次相位、二次相位所带来的不利影响，且一次相位和二次相位的补偿精度应分别满足式(6)和式(8)[7]。

选取某型雷达进行频率捷变信号的二维成像处理，设置随机捷变个数N为64个，载频f0=9.5 GHz，频率捷变间隔Δf=4 MHz，脉冲调频带宽为5 MHz，载频带宽为256 MHz，脉冲重复周期Tr=50 μs，代入式(4)、式(6)计算可得|ΔV1|≤2.4 m/s，|ΔV2|≤45.78 m/s。在成像处理中采用附加测速信息的运动补偿方法，由系统参数可知，该系统的测速精度可以满足一次相位和二次相位误差的补偿精度要求。

2.2 频点缺失对成像效果影响分析

对于随机频率捷变而言，由于捷变频点的完备性较差，不能保证捷变带宽内的每个频点都能发射出去，且同一个频点不具有唯一性。由此带来的问题就是合成带宽内有缺失，且缺失多少无法预知，频点丢失和频点重复导致合成带宽变小，同时捷变间隔不固定，使得合成后的一维像受栅瓣影响较严重。

借鉴调频步进频信号成像处理方法，对频率捷变信号的距离成像处理先是进行子脉冲匹配脉压处理，再对子脉冲压缩后的值分别进行IFFT，然后将处理得到的结果按照目标抽取算法依次拼接起来，就得到目标的一维距离像。该方法运算比较简单，但是受捷变间隔影响，有时会产生栅瓣，导致副瓣(包括旁瓣和栅瓣)较高，会淹没弱目标或被认为是新目标。

距离像处理主要进行脉压处理，可以得到频率捷变信号的自相关函数为[8]：

(9)

式中，τ为回波时延；Tp,n为子脉冲宽度；Bn为子脉冲带宽。该自相关函数由两项组成，|R1(τ)|为线性调频信号的自相关函数，是一个辛格函数，|R2(τ)|与频率捷变信号有关。因频率捷变信号总是fTp,n>1，自相关函数中必然会出现栅瓣。而要想抑制栅瓣，可以通过调整捷变间隔，使|R2(τ)|产生的栅瓣峰值与|R1(τ)|零点的位置相对应。

图2 捷变间隔对栅瓣的影响

假设捷变信号子脉冲带宽10 MHz、脉宽50 μs，捷变点数128，捷变间隔分别取值为4 MHz和5 MHz，对不同捷变间隔下的栅瓣进行仿真分析，如图2所示。

从仿真结果来看，不同的捷变间隔，合成一维距离像的栅瓣输出不同。对频率捷变信号频点重排后，因部分频点缺失或频点重复，使得频率间隔不固定，且频率间隔的变化具有随机性，使得栅瓣抑制更加困难，合成距离像受栅瓣影响严重，对成像质量影响较大。

3 成像效果分析

3.1 速度补偿对距离像影响分析

仿真条件：雷达工作于X波段，信号带宽为5 MHz，选取频率捷变间隔为4 MHz，子脉冲个数为128，模拟目标由4个散射点组成，速度值为10 m/s。合成带宽为512 MHz，合成后距离分辨率为0.292 m。为了更加准确说明速度补偿对成像效果的影响，该仿真中频率捷变频点完备，不存在频点丢失及重复，图3为仿真结果。

图3 随机频点分布的距离像结果

图3(a)为随机频点分布情况；图3(b)为模拟目标一维距离像；图3(c)为采用随机频率捷变信号处理得到的运动目标一维距离像，由于速度值的影响，距离像发生发散且出现杂乱现象，无法有效对目标进行合成；图3(d)是进行速度补偿后的结果，补偿误差为0.4 m/s，补偿后一维像恢复正常，但由于补偿存在误差，散射点强度有所损失。

3.2 频点缺失对成像影响分析

仿真验证条件：雷达工作于X波段，信号带宽为5 MHz，捷变间隔为4 MHz，子脉冲个数为128，脉冲串个数为64帧，模拟目标由10个散射点组成，转动角速度为0.003 rad/s，合成带宽为512 MHz，合成后距离分辨率为0.292 m。

首先，分析第一种情况，捷变频点具有较好的完备性，能包括捷变间隔内的所有频点且每个频点具有唯一性。图4为仿真结果。

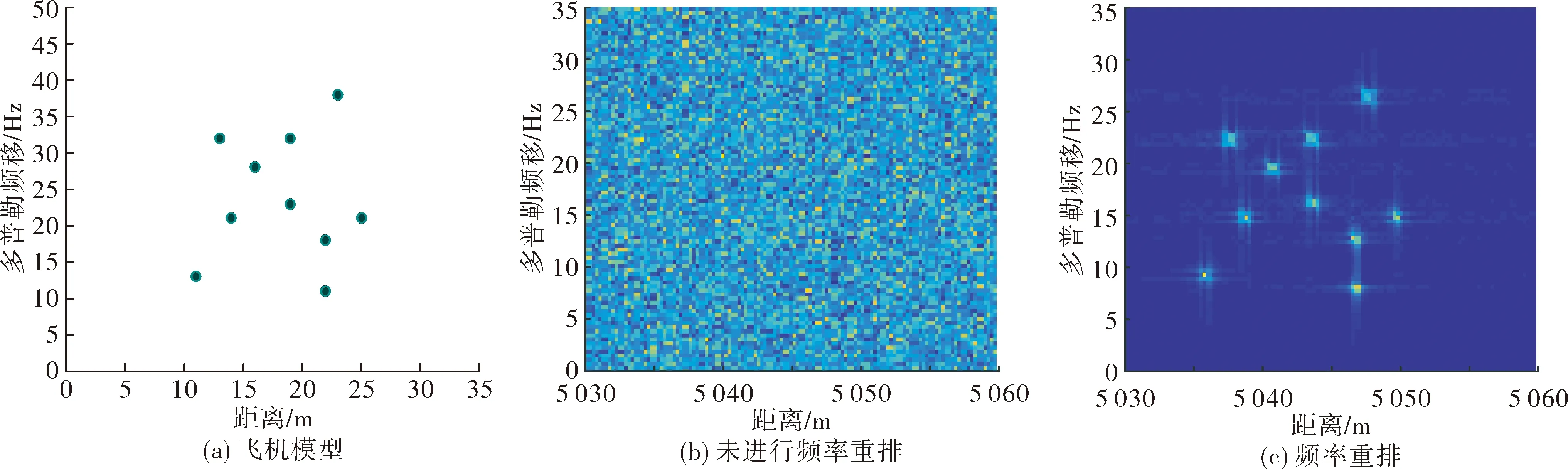
图4 随机频点分布的二维成像结果

图4(a)为仿真设计的飞机模型；图4(b)为未进行频点重排后的二维像，由于频率的随机性，导致二维像在多普勒维散焦严重，无法获取成像结果；图4(c)为进行频点重排后的处理结果，此时无丢失频点，结果和模型相一致。

其次，分析第二种情况，捷变频点完备性较差，捷变带宽内存在频点丢失及重复情况，即每个处理周期中既有重复频点，也有部分丢失频点，同一个频点不具有唯一性。图5为仿真结果。

图5 随机捷变频点分布图

图5(a)为对128个随机捷变信号进行频点重排后的频点分布图；图5(b)为其中一组随机捷变信号频点重排后结果；图5(c)为其局部放大图，可以清晰看出存在频点重复和频带丢失的现象。

下面分别对不同频点缺失数量情况下进行二维成像处理，如图6所示。

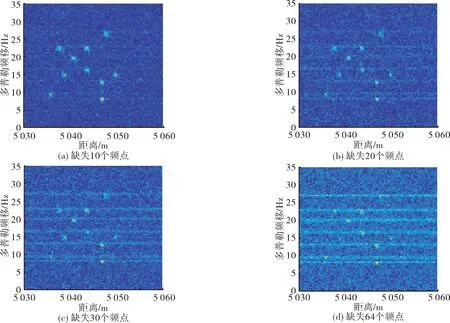
图6 存在频点丢失情况下的二维像

由仿真可知，当捷变带宽内无频点丢失时，能够实现对目标的二维成像，当出现频点丢失时会对成像效果产生影响，丢失频点越多成像效果越差。

3.3 实测数据分析

选取某型雷达进行频率捷变信号的二维成像处理，设置随机捷变信号捷变个数为64，载频带宽为256 MHz，频率捷变间隔Δf=4 MHz，脉冲调频带宽为5 MHz，成像结果如图7所示，未能实现对目标的二维成像。

图7 随机捷变信号二维成像结果

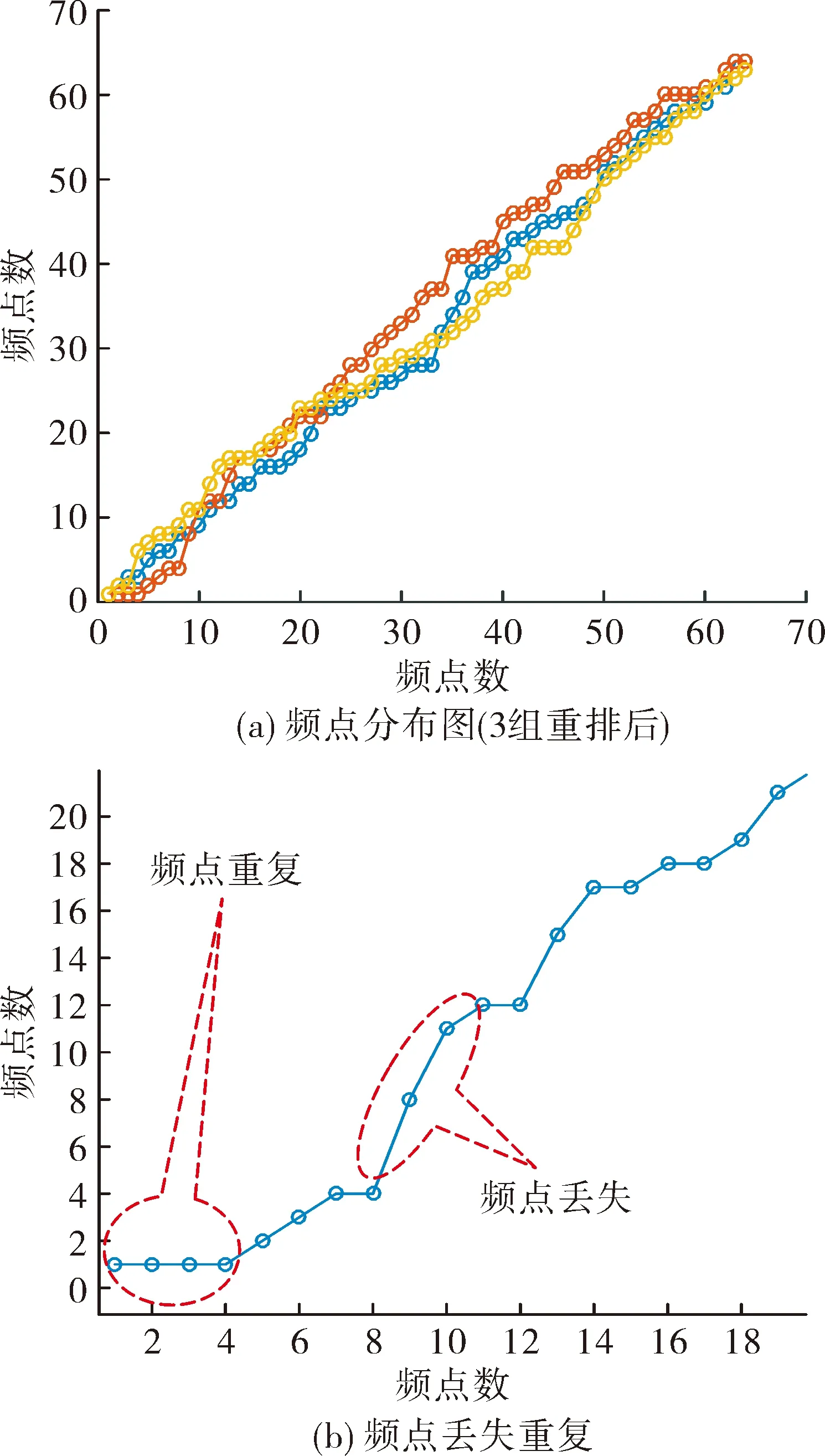
图8 任选3组随机捷变信号频点分布图

对采集的回波数据进行分析，选取任意3帧数据，每帧数据包括一组连续的64个脉冲信号，图8为这任选3帧随机捷变信号的频点分布图，其中图(a)为频点重排后频点分布结果，图(b)为其中一组局部放大图。可以看出，存在频点重复和频点丢失现象，且每组情况都不一样。

由实测数据处理结果可知，采用随机频率捷变信号进行二维成像时，由于实体装备中存在频点丢失和重复，导致捷变间隔发生变化，即Δf=n×4 MHz(n>1)，使得一维成像不满足紧约束条件τΔf<1，在进行一维像处理时，细化后的距离范围减小，无法覆盖回波信号所有散射点，导致距离像出现混叠，一维像之间相关性变差，在紧约束条件下无法形成二维像。

4 结束语

对影响随机频率捷变信号成像效果的原因进行了分析，目标运动所产生的运动速度对成像存在影响，但通过合理的速度补偿能够提高成像质量。在雷达实际工作中，频率捷变信号必然存在频点缺失情况，使得成像效果变差。为了弥补成像效果，可以通过数据拟合插值等方法填充缺失频点数据，但需要经过准确的运动补偿，使得处理算法及处理过程变得复杂。