基于相邻基准子图灰度统计相关的快速互信息匹配算法*

符艳军，孙开锋

(1 西安外事学院，西安 710077； 2 西安精密机械研究所，西安 710075)

0 引言

在基于视觉的飞行器导航与制导、遥感卫星灾害监控与环境监测、医学图像分析等应用中， 常常需要对不同成像传感器获取的异源图像进行匹配。

基于互信息测度的匹配方法是一种完全基于图像灰度统计概率的匹配方法，不需要对原图像间的灰度关系作任何假设，非常适合于异源图像的匹配，但互信息测度最大的缺陷是计算量大， 匹配耗时较长[1]。为此，研究者们就围绕减少互信息测度计算量以及改进搜索策略等方面提出了相应的加速方法。文献[2-5]分别采用模拟退火、粒子群等优化搜索算法提高匹配速度；文献[6]采用灰度压缩和粒子群优化算法相结合加快匹配速度；文献[7]通过提取多层次特征点减少了互信息测度的计算量；文献[8-10]采用由粗到精的多层匹配方法对算法进行加速；文献[11-15]将分层匹配与各种优化算法相结合提高匹配速度。

文中利用匹配过程中相邻基准子图间灰度统计特征之间的相关性，通过差量法减少每一个匹配位置互信息的计算量来加快匹配速度。与已有的以灰度压缩、特征提取或采取优化搜索策略等快速互信息匹配方法相比，该方法既没有减少参与匹配的像素数，也无需对图像灰度等级进行处理，不会对匹配精度造成影响。

1 图像熵及互信息匹配

图像熵描述了图像信源的平均信息量，反映了图像灰度的统计信息，相似的两幅图像其图像熵也相近。利用互信息进行图像匹配的实质是：当两幅图像在空间位置配准时，其重叠部分所对应像素对的灰度互信息达到最大值。 两幅图像U和V的互信息I(U,V)可以用下式表示：

I(U,V)=H(U)+H(V)-H(U,V)

(1)

其中:H(U)、H(V) 分别表示图像U及V的熵；H(U,V)表示两幅图像的联合熵。熵通常由变量的概率密度来表示。针对灰度图像，可以分别用两幅图像的灰度直方图和联合直方图进行估计。 计算公式分别为：

(2)

(3)

(4)

式(2)～式(4)中，hU(i)表示图像U中灰度值为i的像素出现的次数；hV(i)表示图像V中灰度值为i的像素出现的次数；hUV(i,j)表示同一像素位置上图像U中灰度值为i、图像V中灰度值为j的像素对出现的次数；T为图像的总像素数。

研究发现[16]，互信息本身的大小与待配准两图像间的重叠度有一定的关联性，为了消除这种关联关系，文献[17]提出了利用归一化互信息(normalized mutual information， NMI)作为相似性测度。NMI能够减少对图像重叠部分的敏感性，实验表明它比标准的互信息方法更具鲁棒性。NMI表达式为：

NMI(U,V)=(H(U)+H(V))/H(U,V)

(5)

在飞行器导航中，匹配的目的是确定飞行器的当前位置，通过计算实测图与基准图中每一个匹配位置对应基准子图的互信息并找出最大互信息值对应位置，即可确定基准图与实测图的相对位置, 实现对飞行器的定位。

2 快速互信息匹配算法

与基于特征的图像匹配算法相比，基于最大归一化互信息的图像匹配最大缺点是计算速度慢。 每计算一次互信息测度，需要遍历图像中的所有像素，这使得计算量大大增加。由式(5)可以看出，归一化互信息的计算量主要集中在两幅图像各自的熵及其联合熵的计算。从式(2)～式(4)可以看出，图像熵及联合熵均为求和运算，其计算量主要集中于每一个求和项的计算，因此，如果能减少每次匹配过程中需要计算的求和项的项数， 则可以加快匹配速度。因为图像分布具有块状结构，在遍历式搜索匹配过程中，各相邻基准子图的灰度统计量具有很强的相关性，基准图像(i,j)位置处对应子图的灰度直方图与其四邻域位置处对应子图的灰度直方图非常相近。

图1 相邻基准子图及其灰度直方图

如图1所示，图1(a)为原始基准图像，图1(b)为图1(a)的一个子图，图1(c)为图1(b)在原基准图上右移一个像素对应的子图，图1(d)和图1(e)分别为图1(b)和图1(c)的灰度直方图。从图中可以看出，相邻两个子图的直方图非常相似，也即两相邻子图存在大量的灰度值其出现的频率没有发生变化，相应的，在式(2)～式(4)的求和项中分别有很多项数没有发生变化，因此， 当前匹配位置处基准子图的熵以及与实测图的联合熵的计算可以前一匹配位置处基准子图的熵及与实测图的联合熵的计算为基准，通过比较相邻两个匹配位置处基准子图对应的直方图及联合直方图的变化情况，用差量法进行计算。即在整个匹配过程中，除了要完整计算基准图上第一匹配位置(1,1)处对应基准子图的熵以及与实测图的联合熵外，其它所有匹配位置的基准子图的熵及与实测图的联合熵的计算主要集中在与前一匹配位置相比灰度直方图矩阵和联合直方图矩阵中发生变化的那些元素对应的求和项上。据此， 文中互信息匹配算法的流程图如图2所示。具体步骤如下:

1)获取实测图像A和基准图像R，将两幅图像的灰度值调整到同一灰度区间。

图2 文中匹配算法流程图

2)按照式(2)或式(3)计算A的信息熵H(A)并存储。

3)从基准图像R的左上角(1,1)点截取与实测图像A大小相等的第1幅基准子图S1,统计S1各灰度值出现次数并存入初始灰度直方图矩阵hS1，按照式(2)或式(3)计算S1的信息熵H(S1)并存储，最后将hS1和H(S1)分别赋值给hS0和H(S0)。

4)统计实测图A与第1幅基准子图S1对应像素位置的灰度对出现次数并存入初始联合直方图矩阵hAS1，按照式(4)计算初始联合熵H(AS1)并保存，将hAS1和H(AS1)分别赋值给hAS0和H(AS0)；再按照式(5)计算实测图与基准子图的归一化互信息值并存储。

5)从基准图上(1,2)点位置开始，逐行逐像素按照“Z”字形进行迭代匹配。匹配过程中， 当前匹配位置记为(i,j)，当j>1时，当前匹配位置的前一匹配位置应为(i,j-1)；当j=1时，则当前匹配位置的前一匹配位置应为(i-1,j)，则当前位置(i,j)处的归一化互信息可按如下步骤计算:

①通过比较当前匹配位置(i,j)处基准子图和前一匹配位置(i,j-1)或(i-1,j)处基准子图对应列或行像素变化情况，按照差量法将前一基准子图的直方图矩阵hS0更新为当前子图的直方图矩阵hS。具体做法为: 在行方向匹配时，当前匹配位置的前一匹配位置为(i,j-1)，则以hS0为基准，减去前一基准子图第一列对应像素灰度值出现次数，加上当前基准子图最后一列对应像素灰度值出现次数，即得到hS；在列方向匹配时，当前匹配位置的前一匹配位置为(i-1,j)，则以hS0为基准，减去前一基准子图第一行对应像素灰度值出现次数，加上当前基准子图最后一行对应像素灰度值出现次数，即得到hS。

②找出hS与hS0的不同元素，分别组成矩阵hΔS和hΔS0，按照式(6)、式(7)分别计算hΔS和hΔS0对应的信息熵ΔS及ΔS0；其中，normS0(S)为与hΔS0中元素对应的前一基准子图熵值计算过程中的求和项，因为这些求和项在前一匹配位置已经计算过，此次无需再重复计算，而只需计算这些项的和即可。

(6)

(7)

③以前一基准子图的信息熵H(S0)为基准，按照式(8)通过差量法将H(S0)更新为当前基准子图的信息熵H(S)。

H(S)=H(S0)-ΔS0+ΔS

(8)

④计算实测图与当前基准子图的联合直方图矩阵hAS，找出hAS和前一基准子图联合直方图矩阵hAS0的不同元素，分别组成矩阵hΔAS和hΔAS0，按照式(8)、式(9)分别计算hΔAS和hΔAS0对应的联合熵ΔAS及ΔAS0；其中，normAS0为与hΔAS0中元素对应的前一基准子图联合熵计算过程中的求和项，因为这些求和项在前一匹配位置已经计算过，此次无需再重复计算，而只需计算这些项的和即可。

(9)

(10)

⑤以前一基准子图的联合熵H(AS0)为基准，按照式(11)通过差量法将H(AS0)更新为当前基准子图的联合熵H(AS)。

H(AS)=H(AS0)-ΔAS0+ΔAS

(11)

⑥按照式(12)计算实测图与当前基准子图的归一化互信息。

NMI(A,S)=(H(A)+H(S))/H(A,S)

(12)

6) 遍历整个基准图，选取归一化互信息最大值对应的位置作为最终匹配点。

3 算法时间复杂性分析

文中算法与传统方法相比，计算量的差别主要体现在每一个匹配位置处基准子图各统计量的计算上，为此只分析基准子图各统计量计算的时间复杂度。

设基准图尺寸为N×N，实测图尺寸为n×n，则基准子图大小与实测图大小一致均为n×n。

1)基准子图直方图计算

每一个匹配位置处，传统算法需要遍历整个基准子图来计算该子图的直方图，而文中方法只须遍历基准子图的第一行(或列)和最后一行(或列)即可获得该子图直方图。对于整个匹配过程来说，传统方法其时间复杂度为O((N-n)2n2)，文中方法时间复杂度为O((N-n)2n)。

2)基准子图熵及联合熵计算

由于相邻基准子图其直方图发生变化情况跟图像内容有关，很难从理论上推导两子图间有多少个灰度值其出现频率会发生变化，也很难推导出其联合直方图中有多少个灰度值对的频率会发生变化。以直方图为例，最坏情况时有2n(n为基准子图各边长所含像素个数)个灰度值频率发生变化，且2n不超过基准图灰度等级数。

为此，文中在标准图像集上进行了大量的仿真实验，通过对仿真结果进行统计得出：相邻子图间灰度直方图中发生变化的元素平均为50%左右，联合灰度直方图中发生变化的元素平均为75%左右，这就意味着文中方法相比传统方法，其基准子图熵值的计算量减少了近50%，联合熵计算量减少了约25%，时间复杂度或时间频度有所降低。部分实验结果列于表1～表4。

另一方面，因文中方法需要存储前一匹配位置基准子图的多个统计量，算法的空间复杂度有所增加，但由于硬件技术的发展大大提高了计算机的存储容量，使得存储容量的局限性对于算法的影响大大降低。

4 仿真实验

为了验证算法的有效性，将文中方法应用于SAR与可见光图像匹配，以Matlab R2015为仿真平台，进行两类实验：一类是通过比较每个匹配位置处文中方法与传统遍历式互信息匹配方法在计算量方面的差别以及总耗时来说明文中方法的有效性；另一类是将文中方法与多分辨率分层匹配相结合，与单纯的多分辨率方法进行匹配耗时及匹配精度的比较，其中的多分辨率分层匹配采用d3小波基，小波分解级数为1。限于篇幅，文中只列出部分结果。

匹配过程中设: 基准子图直方图计算中需要统计的像素灰度值的次数为M，基准子图熵值计算中需要计算的求和项的项数为M1，基准子图与实测图联合熵计算中需要计算的求和项项数为M2。

选取可见光与SAR图像进行匹配，如图3所示，其中图3(a)为可见光基准图，大小为422×358；图3(b)为SAR实测图像1，大小为150×150，图3(c)为SAR实测图像2，大小为100×90，图3(d)为基于文中差量法匹配时实测图在基准图上的匹配定位结果；表1为差量法与传统标准算法列方向匹配时部分匹配位置计算量统计结果的比较，表2为差量法与传统标准算法行方向匹配时部分匹配位置计算量统计结果的比较，表3为文中差量法与传统标准方法匹配结果和匹配耗时的比较，表4为差量法结合多分辨率分层匹配法与单纯多分辨率分层匹配法的匹配结果和匹配耗时的比较。

图3 SAR与可见光图像匹配

由图3可以看出，采用归一化互信息作为匹配测度，可以实现异源图像之间的匹配；由表1～表3可以看出，相比传统方法，文中差量法能够有效减少除第一个匹配位置外其它所有匹配位置互信息测度的计算量，总匹配耗时平均减少20%以上；由表4可以看出，文中差量法可以与多分辨率分层匹配技术相结合，其匹配精度与单纯的多分辨率分层匹配算法精度相同(在有些情况下匹配精度有所下降)，但其匹配耗时平均下降20%左右。

5 结语

与已有的以灰度压缩、特征提取或采取优化搜索策略等快速互信息匹配方法不同,文中基于图像的块状结构特性以及匹配过程中相邻子图统计特性的相关性, 通过差量法减少互信息测度的计算量来加快匹配速度, 其互信息测度计算精度及匹配精度与原始的基于标准互信息计算方法的计算精度及匹配精度相同, 但计算量大为减少。 另外,如果参与匹配的两幅图像为高分辨率清晰图像，则可以把文中方法与灰度压缩、多分辨率分层匹配等方法相结合，即先对待匹配的图像进行灰度压缩或多分辨率分解，然后采用遍历式方法进行搜索，而在每一个搜索点处采用文中的差量法计算互信息测度，这样可以进一步减少匹配耗时。

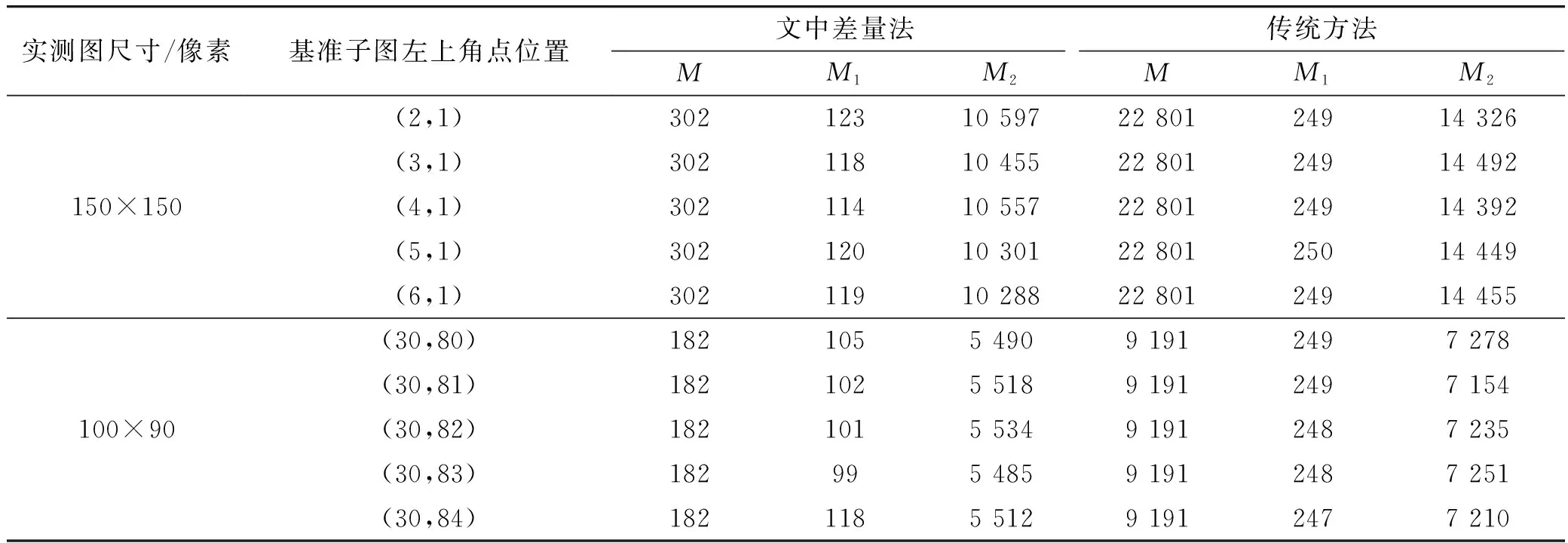
表1 SAR与可见光图像在列方向匹配时部分位置计算量统计结果

表2 SAR与可见光图像在行方向匹配时部分位置计算量统计结果

表3 差量法与传统标准法在SAR与可见光图像上的匹配结果

表4 差量法结合多分辨率分层算法与单纯多分辨率分层算法在SAR与可见光图像上的匹配结果