多弹协同拦截制导律设计*

肖念远，王晓芳，周 健

(1 北京理工大学宇航学院，北京 100081； 2 西安现代控制技术研究所，西安 710065)

0 引言

近年来，空战武器和一体化防空系统飞速发展，战场形式日益立体化、复杂化[1]。无人战机作为重要军事目标，配备多层次防御体系必要且紧迫[2]。传统空中防御措施有被动防御(即机动躲避)、主动防御(即释放红外干扰弹等)[3]。防御弹机动性能和毁伤能力受限，仅靠单枚弹难拦截敌方袭击，使得防御可靠性下降。

运用先进技术，无人战机发射多枚防御弹主动防御，组成协同防御系统，能更有效的拦截[4]。设计满足需求、适应战场环境的协同拦截制导律，成了制导技术的研究热点。协同拦截制导律的主要研究对象有我方目标(无人战机)、一枚或多枚防御弹、敌方来袭弹。针对目标、来袭弹、防御弹的“三体”[5]问题，一般作为两个并行制导问题，即来袭弹攻击目标、防御弹拦截来袭弹[6-7]。文献[8-9]研究了多枚导弹拦截来袭弹，但所需过载较大。一般情况下，来袭弹机动性能大于防御弹机动性能，存在脱靶量大，拦截失败的可能。文献[10-13]提出了不同种类的协同拦截制导律，但建立在线性化基础上，需预估剩余飞行时间，且拦截的多为静止目标，不满足现代战争需求。

文中针对该情景，提供一种新的协同拦截思路。建立非线性运动方程组，基于极小值原理和动态逆理论设计两种制导律，让无人战机顺序发射两枚防御弹，防御弹DA与无人战机采用最优协同制导律OCGL，防御弹DB采用时间协同制导律TCGL，以减小防御弹DA的过载需求，实现两枚防御弹同时拦截来袭弹，对防御弹发射间隔进行优化，使防御弹DB的拦截能量小且和DA打中M的拦截间隔相差小。

1 问题描述

假设来袭弹、目标(无人战机)、防御弹在铅垂面内运动，如图1所示。

图1 来袭弹-防御弹-目标相对运动示意图

图中，OXY为惯性坐标系，M、T、Di(i=A, B)分别为来袭弹、目标、目标发射的防御弹。Vj、aj、θj(j=M,T,Di)分别表示速度、垂直于速度矢量的加速度和弹道倾角。rMDi和rMT表示M与DA、DB、T之间的距离，qMDi和qMT为对应的视线角。uj为加速度矢量在垂直于视线方向的分量，u′MDi为M加速度在垂直于M-Di视线方向的分量。

M、Di和T的相对运动方程组为：

(1)

设M采用增强比例导引[14](APN)，则

(2)

式中，KM为M的制导系数。

2 协同拦截制导律设计

T顺序发射DA和DB，T与DA以OCGL飞行，T协同，吸引M飞向DA，DA以小过载拦截M。基于动态逆理论[15-16]，令DB以TCGL飞行，DB-M弹目距离与DA-M趋于一致，与DA同时拦截M。

2.1 非线性OCGL设计

由式(1)可知DA与M相对运动方程组为:

(3)

对式(3)求导得:

(4)

(5)

(6)

由图1可知，u′M与uM之间的转换关系为:

(7)

式(7)代入式(6)可得状态方程为：

(8)

(9)

式(9)中，t1、tf为DA的发射和终止时刻，终端指标和动态指标的权重系数分别为a、b、c，有a≥0,b≥0,c≥0。

由性能函数和状态方程得汉密尔顿方程：

(10)

式中，λ为协态量，正则方程和横截条件为：

(11)

由极小值原理可知：

(12)

联立可得最优控制的开环解为：

(13)

将式(13)代回状态方程积分化简可得：

(14)

将式(14)代入式(13)，得到采用OCGL的DA和T控制指令的闭环解。

2.2 多防御弹TCGL设计

T发射DA后，再发射DB，DB与DA同时命中M。基于动态逆理论，rMDB与rMDA趋于一致，可实现DA和DB的拦截时间协同。

定义弹目距离跟踪误差为：

(15)

对式(15)求导可得:

(16)

令实际速度前置角ηDB=qMDB-θDB。基于动态逆理论，设计期望速度前置角ηc为：

(17)

式中，Kr>0为衰减系数。当ηDB=ηc后，联立式(16)和式(17)得，呈指数衰减，DB的弹目距离趋于实现时间协同。

令E=cosηc，反解ηc为：

(18)

式中：η0为DB的初始速度前置角；ηmax为DB的最大速度前置角。

由于ηDB=qMDB-θDB，求导可得：

(19)

基于动态逆理论设计θDB为：

(20)

式中Kη>0，为衰减系数。

为保证制导精确，考虑DB的导引头识别距离、制导时间等因素的影响，令DB与M的弹目距离为Δr1时，转入APN为：

(21)

式中，KDB为APN系数。

3 发射时间优化设计

受发射技术和战场环境制约，DB无法与DA同时刻发射，假设T先发射DA，再发射DB。由于DB末制导转APN，故DA、DB到达M的时间有误差，通过文化算法计算两枚防御弹发射间隔的最优解，使拦截间隔和DB能量小。

令DA发射时间为t1，DB发射时间为t2，发射间隔为Δt1=t2-t1，优化函数为:

(22)

式中:|Δt2|为DA和DB拦截M的时间差；为DB的控制能量；相应权重d>0，e>0。

设计变量Δt1的边界约束条件为：

Xmax=Δt1，max，Xmin=Δt1，min

(23)

式中，Δt1，max和Δt1，min为DB发射时间上下限，由战场形势与技术能力决定，故优化模型的可行域为：

Ω=[Xmin,Xmax]

(24)

令过载需要满足的过程约束为:

gj(X)=|nj|-njmax≤0,j=M,T,DA,DB

(25)

式中：nj为需用过载；njmax为可用过载。

综上分析，发射间隔优化模型为：

(26)

优化模型建立之后，即用文化算法进行优化，得到Δt1的最优解，进而得到DB的发射时间t2=t1+Δt1。

4 仿真分析

4.1 OCGL仿真结果及分析

设t1=0，KM=4，a=1010,b=0.1,c=1。其余条件见表1，仿真结果如图2～图4所示。

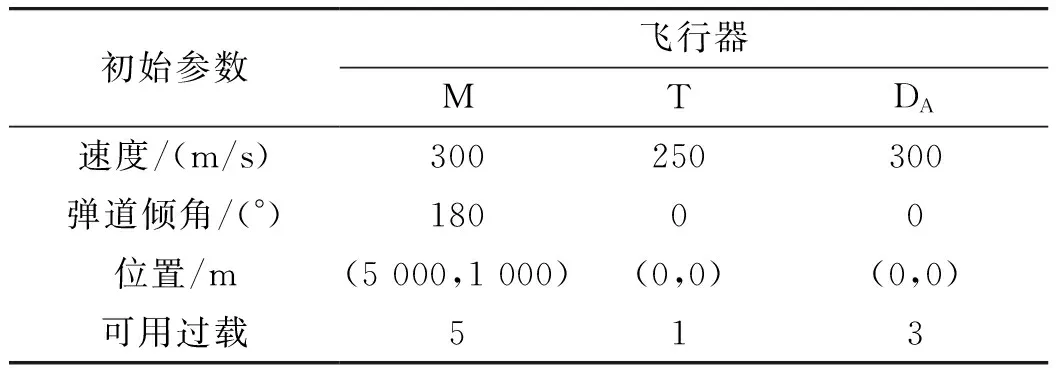
表1 OCGL仿真初始条件

图2 OCGL弹道图

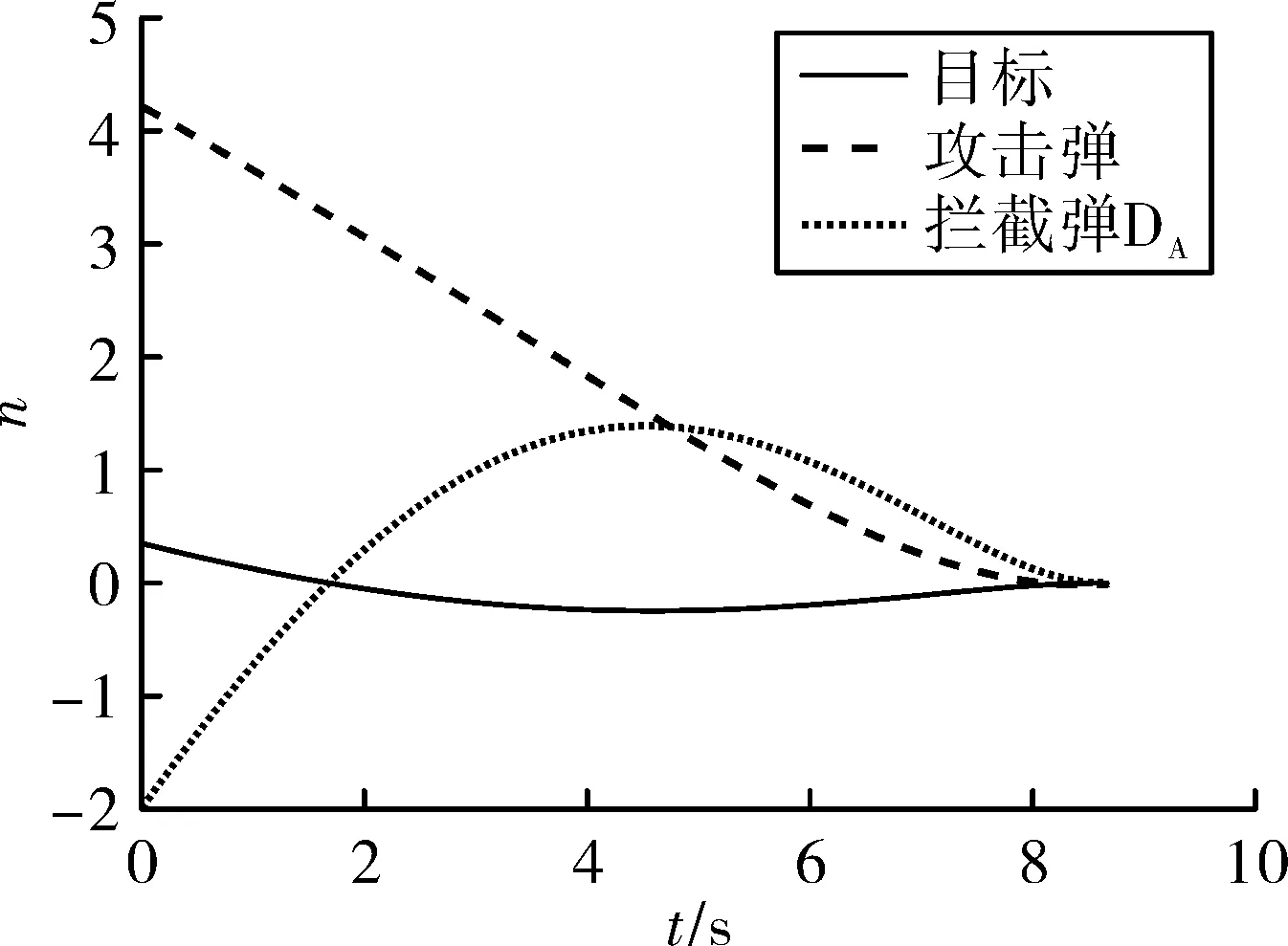
图3 OCGL过载随时间变化图

图4 OCGL视线角速度随时间变化图

由图2知,在OCGL导引下，T向y轴负方向飞行，引诱M飞向DA。由图3知，机动能力小的T和DA，成功拦截过载较大的M。图4所示视线角速度均趋于零，表示OCGL实现对视线角速度的控制。该组结果证明OCGL可以实现低过载防御弹对高过载来袭弹的拦截。

4.2 TCGL仿真结果及分析

在表1的基础上，令t2=0.5 s，VDB=320 m/s，KMDB=4，Kη=5，Kr=1，ηmax=30°，Δr1=700 m，ηDBmax=20。仿真结果如图5～图8所示。

图5 TCGL弹道图

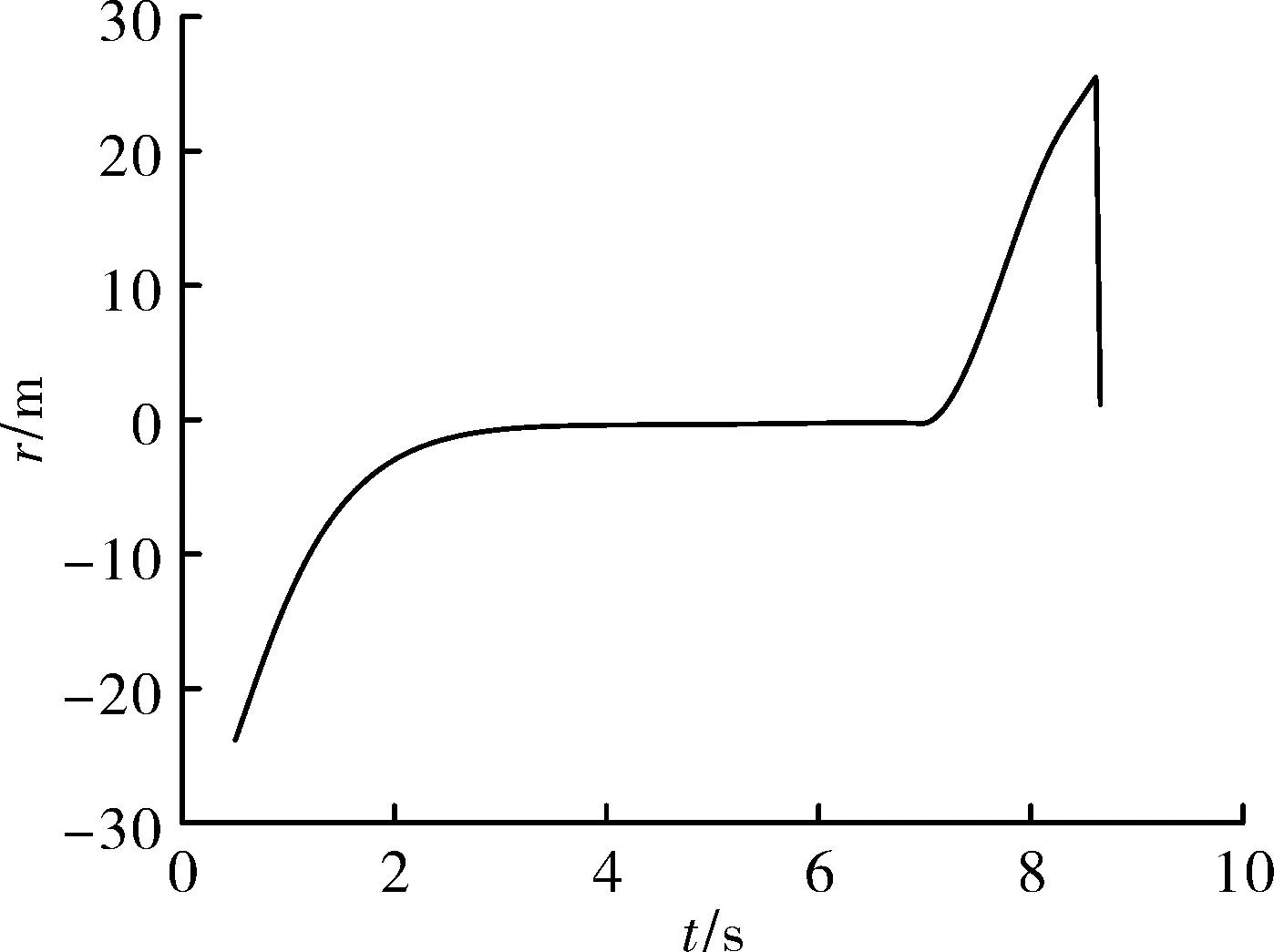
图6 DA和DB的弹目距离差随时间变化图

图7 DB速度前置角变化图

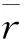
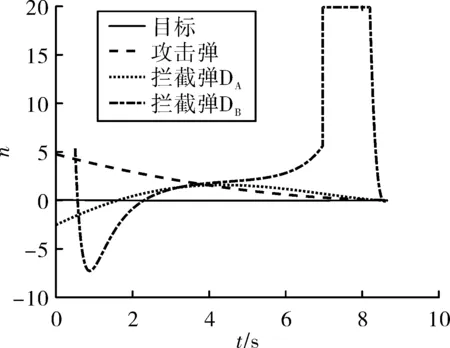
图8 TCGL过载变化图

4.3 Δt1优化结果及分析

结合上面分析，对Δt1进行优化。令d=0.01，e=1 000。设置经过20代迭代，每代10次寻优。边界约束条件为：0.1 s≤Δt1≤5 s。其余仿真参数同上。

设计不同情形以研究Δt1的影响，场景2为d=0.01，e=0.01；场景3为d=0.001，e=1 000，场景2、3与前述场景1，即d=0.01，e=1 000，优化结果对比如表2所示。

表2 3种场景下的优化结果

对比场景1和场景2，当e减小时，DB付出的能量相对于场景1减小2%。由场景1和场景3可知，当d减小时，|Δt2|=0 s，两枚防御弹同时拦截M，参数d的改变对于整体结果影响较小，是由于Δt2较小，对于结果影响相对较小导致的。在该场景下，选取发射时间间隔为2.3 s左右即可实现最优。改变优化参数对于结果的选取影响不大，从侧面证明了TCGL的适应性和参数的合理性。

5 结论

提出了一种新的协同防御策略。无人战机顺序发射两枚防御弹，设计OCGL和TCGL拦截来袭弹，优化防御弹发射间隔，针对不同场景得到对应最优解。证明了OCGL拦截来袭弹的过载优势，TCGL可实现两枚防御弹同时拦截来袭弹，组合使用能增加对来袭弹的毁伤力度。