具有时滞的脉冲随机神经网络的有限时间稳定性
鲁成甜,喻 圣,程 培
(安徽大学数学科学学院,安徽合肥 230601)
1 引言
近几十年来,神经网络模型得到了广泛的研究,在信号处理、联想记忆、模式识别和组合优化等方面都有应用,吸引力大量学者的关注.而在神经网络模型中由于神经元之间的相互作用不同步性或信号传输速度的有限性,不可避免地会产生时滞.因此,研究具有时滞的神经网络的稳定性具有重要意义[1].而脉冲描述了系统状态的瞬时跳变或重置,也是引起系统不稳定和性能差的主要原因之一[2].再者,对于实际系统,随机噪声扰动的影响也是不可或缺的[3],为了准确地描述系统,从而设计出好的控制方案,研究系统的稳定性需要充分考虑随机噪声扰动的影响.由于同时考虑了脉冲和随机噪声扰动两个因素的影响,具有时滞的脉冲随机神经网络的稳定性分析相对比较复杂.因此,该系统的稳定性的研究具有理论和现实的重要意义.
另一方面,众所周知,在系统稳定性理论的研究中,往往考虑比较多的是Lyapunov稳定性.Lyapunov稳定性侧重于系统在无穷时间区间上的动态行为,它反映的是系统的稳态性能,而在很多实际应用中只关注系统的稳态性能是不够的,系统的暂态性能也起着很重要的作用,如在两个航天器交会对接过程、卫星变轨过程、飞行器再入过程等方面有限时间稳定性就描述了系统的暂态性能.有限时间稳定是指如果给定初始条件下,系统的状态在一段特定时间区间内始终不超出某个特定区域.它的概念可以追溯到1960年[4-5],经过其后60多年的发展,有限时间稳定性的研究已取得了丰富的结果[6-9].Ali等人利用一个新的Lyapunov-Krasovskii 泛函和线性矩阵不等式(linear matrix inequalities,LMIs)工具分析了Cohen-Grossberg神经网络的随机有限时间稳定性[10].Lee等人利用平均脉冲区间条件研究了非线性脉冲系统的有限时间稳定性问题[11].Zhu等人利用多重Lyapunov-like函数考虑了具有时变时滞的非线性脉冲随机系统的均方有限时间稳定性[12].尽管关于各类系统有限时间稳定性问题的研究已有不少成果,但值得注意的是,关于同时考虑脉冲和随机噪声扰动的神经网络的有限时间稳定性的结果不多见.
因此,本文利用平均脉冲区间条件,随机分析技巧和Lyapunov泛函结合LMIs工具,研究具有时滞的脉冲随机神经网络的均方有限时间稳定性问题,对反镇定型、中立型和镇定型3种类型的脉冲分别给出系统有限时间稳定的充分条件.最后通过一个数值例子验证了理论结果的有效性.
2 准备知识
本文采用以下记号:记(Ω,F,{Ft}t≥0,P)为一完备概率空间,{Ft}t≥0为一满足通常条件的σ代数流,ω(t)为定义在该空间上的1维布朗运动,上标T表示向量或矩阵的转置,∗表示矩阵中由对称性得到的元素.λmax(·)为实对称矩阵的最大特征值,diag{·}为对角矩阵,tr{·}为矩阵的迹,I为适当维数的单位矩阵,P>0(≥0)表示P是正定(半正定)矩阵,P <0(≥0)表示P是负定(半负定)矩阵,E{·}是期望算子,|·|表示向量的欧几里得范数.
考虑带有时滞的随机脉冲神经网络

其中:x(t)∈Rn是系统的状态,([−τ,0];Rn)是初始条件,A,B,C,D,E,F∈Rn为适当大小的矩阵,
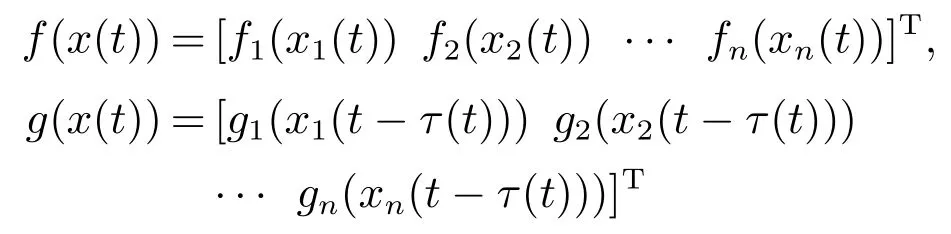
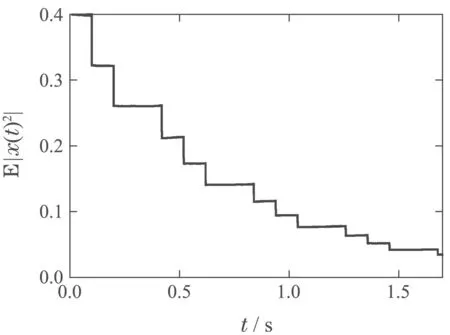
都是神经元激活函数,有f(0)=g(0)=0.时滞τ(t)为时变连续函数且满足0 ≥τ(t)≥τ,(t)≥h<1.{tk}k∈N是脉冲瞬时序列满足0 ≥t0 定义1[13]若对于给定正常数c1,c2,T,c1 则称系统(1)关于(c1,c2,T)均方有限时间稳定. 定义2[14]对于脉冲序列{tk}k∈N,若存在正整数N0和正数τ∗,对任意的t ≥s ≥t0,有 则该脉冲序列的平均脉冲区间为τ∗,其中N(t,s)表示脉冲序列在时间(t,s)内脉冲发生的次数. 假设1[15]函数fi是连续的,且存在正常数,(i=1,2,···,n),对∀α,β∈R,αβ,有 假设2[15]函数gi是连续的,且存在正常数,(i=1,2,···,n),对∀α,β∈R,αβ,有 情形1µ≥1. 定理1假设脉冲序列满足式(3),给定正数T,c1和c2(c1 证选取Lyapunov泛函 当t=tk时,结合系统(1)的第2个等式和式(5),有 由假设1-2可知 对∀t∈[tk,tk+1),k=0,1,2,···,由It’s公式可得 对式(11)两边从tk到t积分再取期望结合Gronwall不等式得 通过式(9)有EV(tk)≥µEV(),结合上式进行迭代运算可以得到 由定义2结合式(6)-(7)得 因为λ2|x(t)|2≥V(t),所以通过上式可得 所以由式(2)知系统(1)关于(c1,c2,T)均方有限时间稳定. 证毕. 注1当µ>1时是反镇定型脉冲即脉冲不利于神经网络的稳定性.这时式(6)等价于 由此可以看出要求平均脉冲区间不能太小即脉冲不能发生太频繁;同时要求 即需要神经网络连续部分不能增长太快.当µ=1时是中立型脉冲即脉冲对神经网络的稳定性无影响,此时的神经网络相当于无脉冲作用的连续系统.而 即需要神经网络连续部分不能增长太快. 如果系统(1)中的D=0,E=0即没有随机噪声干扰的因素,则有 推论1假设脉冲序列满足式(3),给定正数T,c1和c2(c1 则系统(12)关于(c1,c2,T)均方有限时间稳定. 注2与文献[15]相比分别讨论了带有时滞的脉冲神经网络的有限时间稳定和全局指数稳定.有限时间稳定和经典的Lyapunov稳定是两个独立的概念,不能相互推导.一个Lyapunov稳定的系统,如果它的瞬时效应超过了规定的界限就不是有限时间稳定的,反之如果不知道超过指定时间间隔的系统状态,则有限时间稳定的系统在Lyapunov意义下可能是不稳定的.这里因为条件α+ln(µ)>0以及证明过程可以看出系统(1)是有限时间稳定的但不是Lyapunov指数稳定的. 情形2µ<1. 定理2假设脉冲序列满足式(3),给定正数T,c1和c2(c1 其中: 则系统(1)关于(c1,c2,T)均方有限时间稳定. 证由定理1知当t=tk时,结合系统(1)的第2个等式和式(14)及式(17),有 其中:t∈[tk,tk+1),k=0,1,2,··· .将式(18)代入式(19),并假设 下面证明这个假设成立:当t∈[t0,t1),N(t,t0)=0时,由式(19)可得成立.当t∈[t1,t2),N(t,t0)=1时,有 则用归纳法可知式(20)成立.再由式(3)和式(15)及式(16)可知 通过上式可得 所以由式(2)知系统(1)关于(c1,c2,T)均方有限时间稳定. 证毕. 注3与定理1相比定理2在处理V(tk)时有所不同,所以对应的式(6)和式(15)不同.当µ<1时,若µ+ρτ <1则式(15)等价于 由式(21)可以看出神经网络连续部分不能增长太快.而式(22)与之相反,因为此时的脉冲是镇定型脉冲即脉冲有利于神经网络的稳定,从而需要平均脉冲区间足够小即式(23). 推论2假设脉冲序列满足式(3),给定正数T,c1和c2(c1 则系统(1)关于(c1,c2,T)均方有限时间稳定. 注4与文献[12]相比本文不仅仅讨论了µ≥1的情况,还讨论了µ<1的情况,同时这里的系统的扩散项是线性的形式. 注5与文献[7]相比都考虑了3种类型的脉冲,但是文献[7]针对的是线性系统,并且本文增加了时滞对系统稳定性的影响,更具有一定的现实意义.另一方面在选取V 函数的时候也有所不同,本文利用了Lyapunov泛函,而文献[7]用的是Lyapunov函数. 考虑系统(1),其中: 通过简单计算可知 令α=2,µ=0.83,c1=0.1,c2=10,T=2,N0=3,利用MATLAB 工具箱求解可得满足线性矩阵不等式(13)-(17)的可行解 本文设τ∗=0.14>0.1330,由定理2知系统(1)关于(0.1,10,2)均方有限时间稳定.当ε=0.1<τ∗时,构建脉冲序列为{ε,2ε,···,(N0−1)ε,N0τ∗,N0τ∗+ε,N0τ∗+2ε,···,N0τ∗+(N0−1)ε,2N0τ∗,···}如图1所示;初始值为x0(s)=(0.6,−0.2)T,s∈[−0.5,0]的2000个状态样本路径对应的均方轨迹如图2所示. 图1 脉冲序列N0=3,τ∗=0.14Fig.1 Impulse sequence with N0=3,τ∗=0.14 图2 系统(1)的均方轨迹Fig.2 The mean square state trajectory of the system(1) 本文研究了具有时滞的随机脉冲神经网络的有限时间稳定性问题.利用平均脉冲区间条件,随机分析技巧和Lyapunov泛函结合LMIs工具,对反镇定型、中立型和镇定型3种类型的脉冲分别给出系统有限时间均方稳定的充分条件.最后通过一个数值例子验证了理论结果的有效性.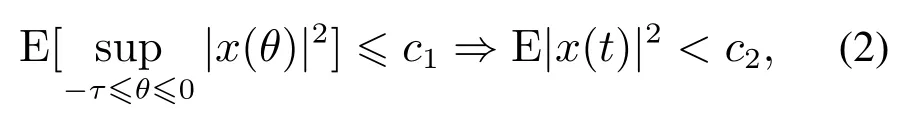
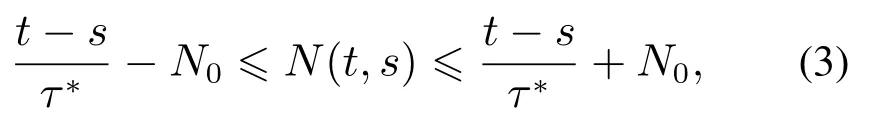
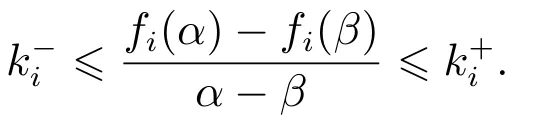

3 主要结果



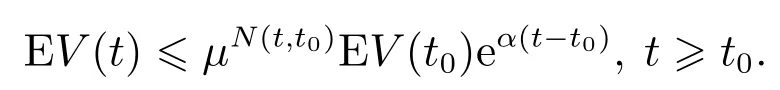
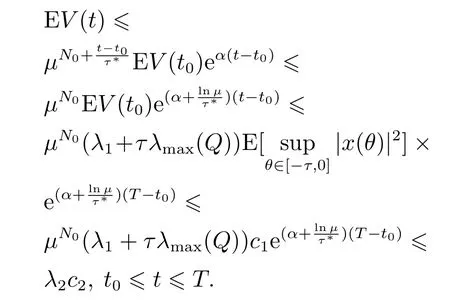
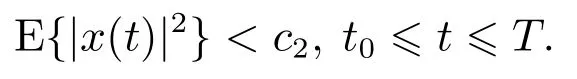
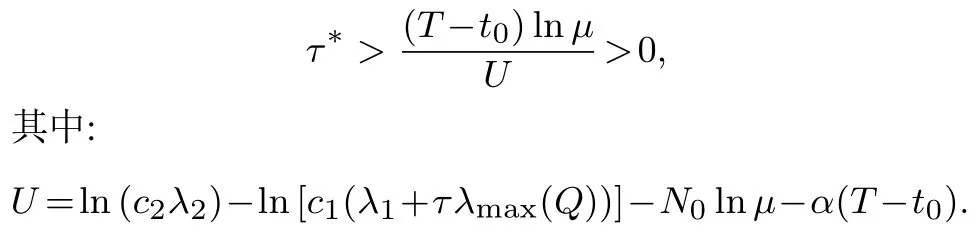
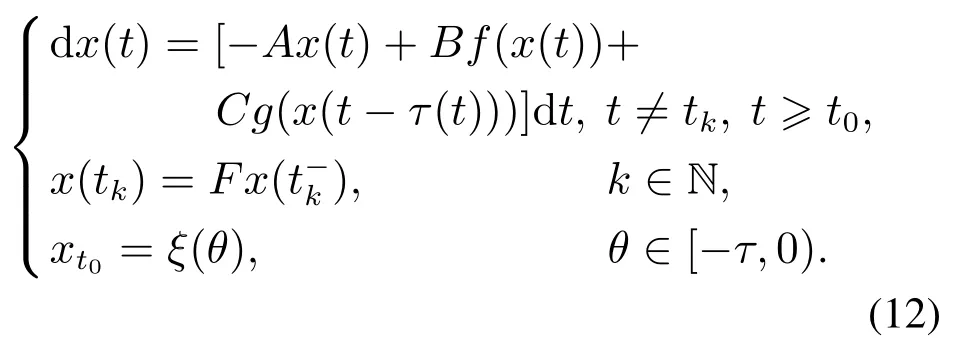

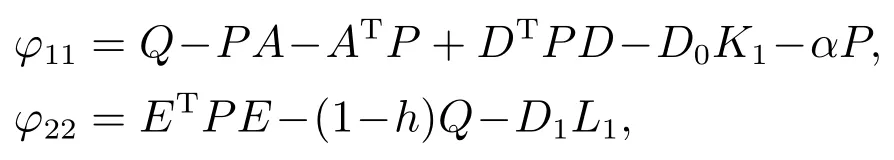
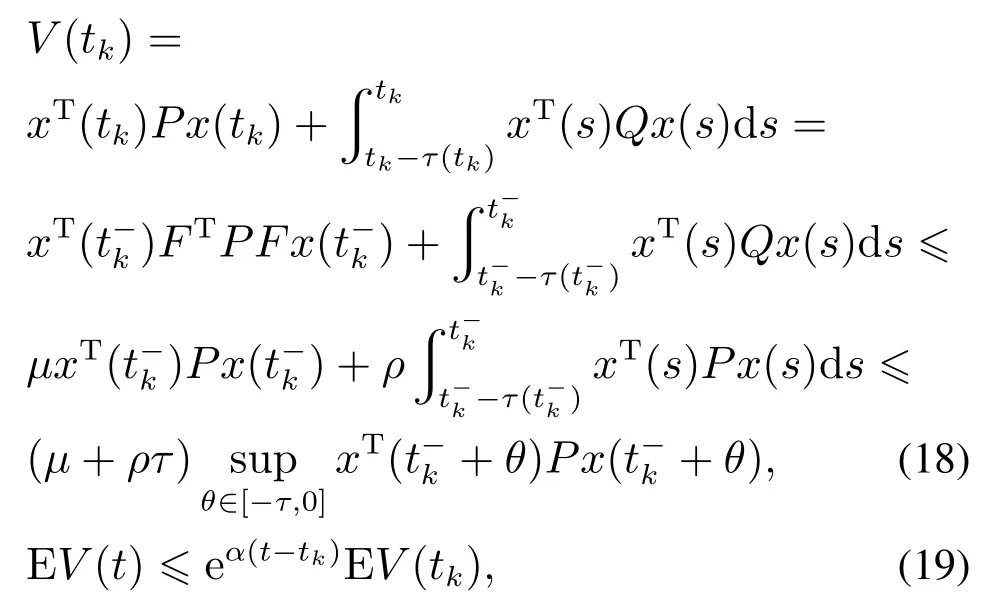
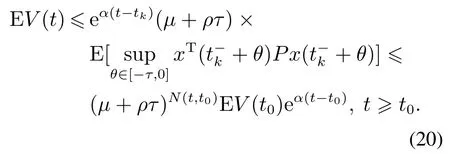
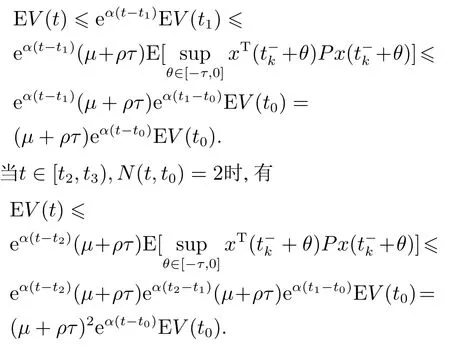
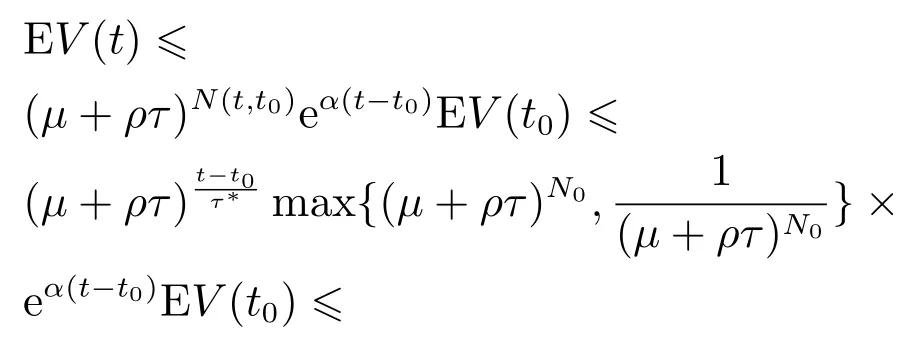
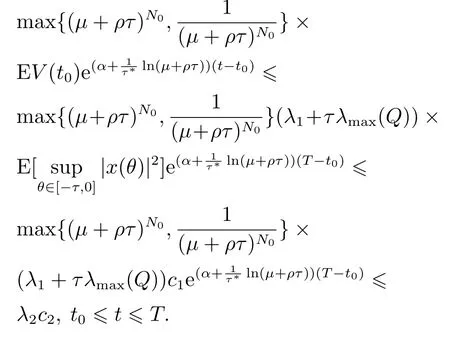
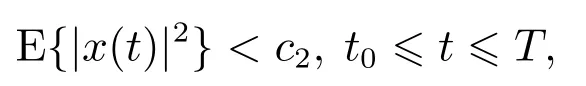
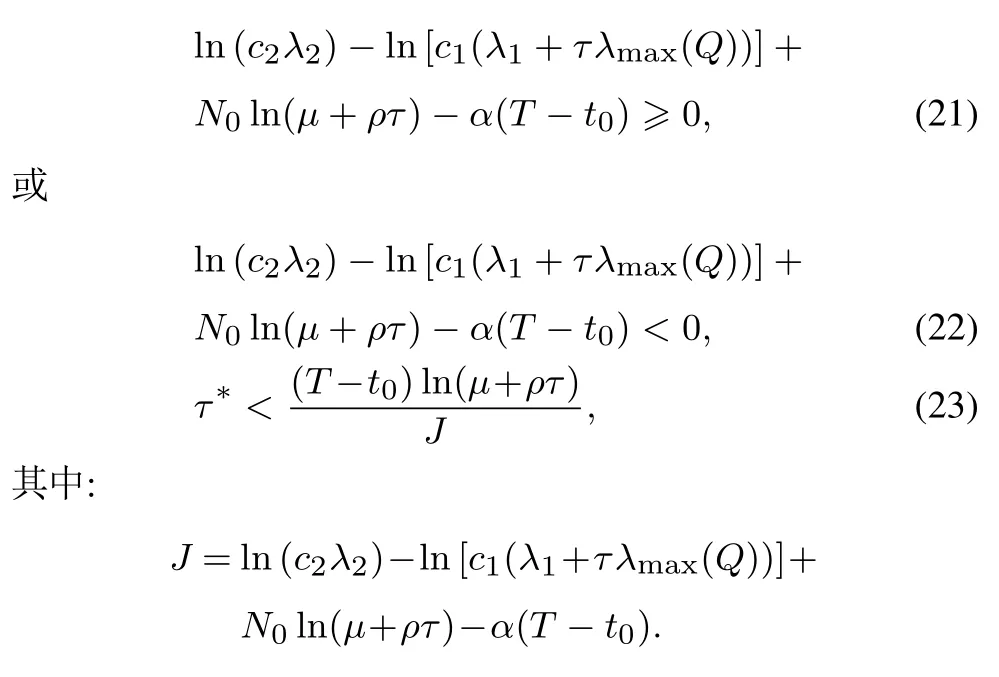
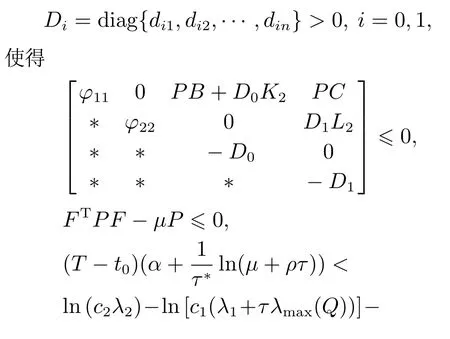
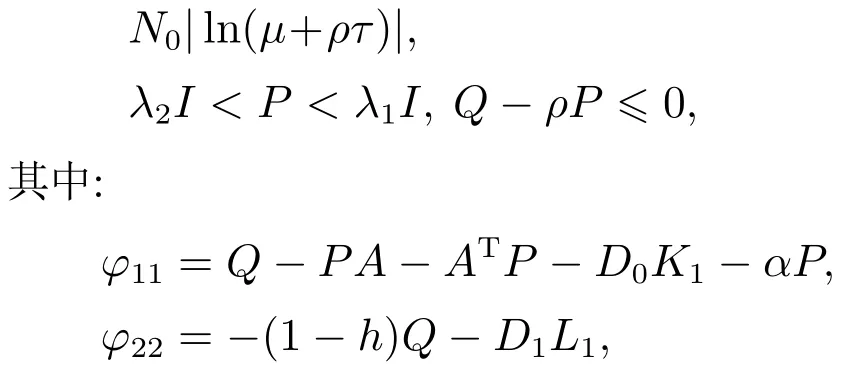
4 数值例子
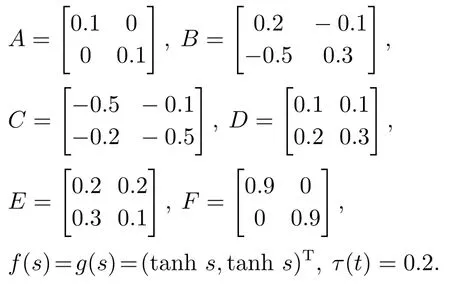

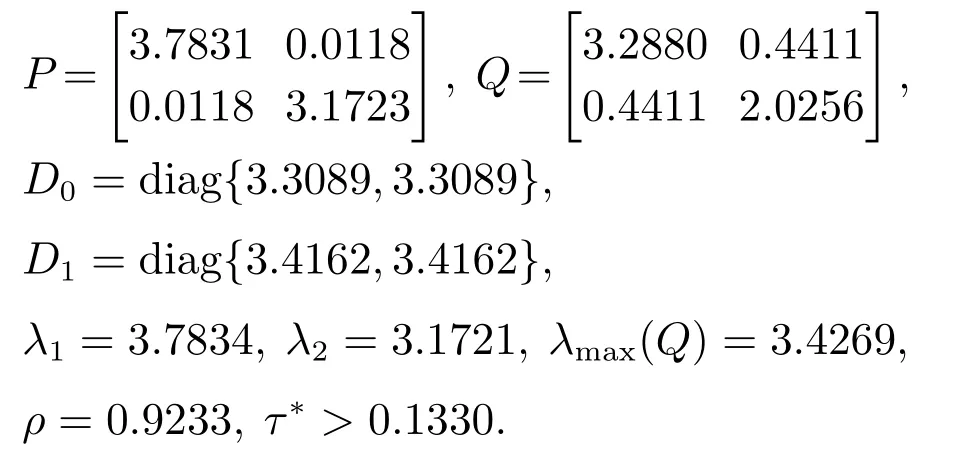

5 结论

