多目标进化算法的污水处理过程优化控制
杨 壮,杨翠丽,顾 锞,乔俊飞
(北京工业大学信息学部计算智能与智能系统北京市重点实验室,北京 100124)
1 引言
在整个污水处理过程中,最终的目标是必须能够使出水水质如化学需氧量、生化需氧量以及氨氮等指标达标[1-3].近年来,我国城镇污水处理厂的污水处理量逐年攀升,与此同时国家对出水水质的严格要求以及节能政策,使得污水处理运行成本不断增加[4-5].由此可见,为了保证污水处理过程中出水水质达标排放,并且降低污水处理过程中的成本费用,实现污水处理过程优化控制是目前污水处理厂亟待解决的问题.
污水处理优化控制的目的为在出水约束的条件下实现节能降耗,其控制运营的总成本主要包含两方面:系统能耗和由出水水质超标而造成的罚款.这两个评价指标在污水处理控制过程中相互矛盾,其中众多变量又受到指标限制,所以研究出一种能够处理多目标优化问题的方法对于污水处理控制过程有着重要意义[6-8].
现在越来越多的优化算法被深入研究,其中遗传算法是将生物界中“优胜劣汰”的思想引入到优化算法中,使种群中适合环境的解能够保留下来,并进行进化和突变,最终得到的种群能够更加适合当前的环境[9-11].但是就像污水的处理过程中的出水水质和系统能耗一样是一对相互矛盾的目标指标,很多优化问题需要针对多个目标问题进行同时优化[12].与单目标相比,多目标优化问题在进行简单搜索过程中找不出对于多目标问题的优秀解.如公式(1)表示的是多目标问题的通用函数:
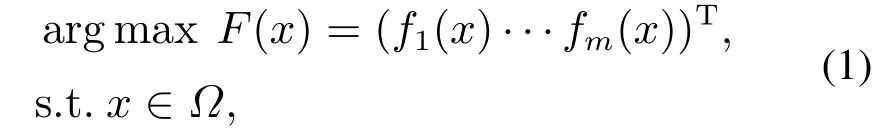
F(x)是由m个f(x)问题组成的多目标优化问题.其中目标函数fm(x)之间常常相互冲突,用单目标优化方法计算得到的解通常不能使每个目标函数同时达到最优.为了解决这一问题,提出了针对多目标优化问题的进化算法.
在多目标优化的问题中,能够满足优化目标的解在一般情况下有很多个,这些个体组成的种群构成帕累托最优解.对于多目标问题之间出现矛盾的问题,张等人提出一种基于分解的多目标优化进化算法(multi-objective evolutionary algorithm based on decomposition,MOEA/D)[13]:该算法将多目标优化问题分解为N个子问题,求解单个子问题就是单目标优化问题或者优化单解的问题.该方法能够在解决一些多目标问题时,近似找出帕累托前沿.在此之后有很多学者基于此框架下对多目标优化算法进行了更加深入的研究[14]:柯等人将启发式蚁群算法融合到MOEA/D框架中,将分解的子问题分配给蚂蚁子群,通过启发式信息矩阵进行最佳方案的搜索,结果表明算法的收敛性有所提高[15];齐等人通过动态调整权重向量的大小,从而使得种群的多样性有所改善[16];周等人通过分析分解的子问题的重要程度,来决定优化的方向,从而使得种群的收敛速度加快[17].
目前对多目标遗传算法性能的提升仍是重要的研究,所以针对污水处理过程中的多目标优化问题,本文通过对MOEA/D算法进行改进,在其基础上进行二次寻优(secondary search,SS-MOEA/D),实验结果表明能够使MOEA/D算法的性能有所提高.利用改进的算法使在权衡能耗和出水水质的多目标问题中找到的解能尽可能分布均匀,获得溶解氧和硝态氮浓度最优设定值,解决了优化控制过程变量繁杂,难以实现实时优化的难题.
2 污水处理过程分析
2.1 仿真模型
污水处理过程是一个庞杂的非线性动态系统,反应过程中包含了一系列物理和生化反应,流量和负荷都会对整个系统造成巨大的扰动,污水处理厂要必须保证系统安全连续运行,所以在实际的污水系统中比较控制方案的优劣显然是不可行的.为了证明控制方案的可行性以及优劣性,需要对污水处理厂的环境进行仿真模拟.由国际水协会与欧盟科学技术合作组织合作开发的污水处理“仿真基准模型(benchmark simulation model 1,BSM1)”[18-19],是当前国际上公认的对污水处理过程的测试平台,其整体布局如图1所示.
该基准模型选用的设备结构是一种相对简单,但已得到普遍应用的布局,由1个生物反应器单元和1个二沉池单元组成.其中生物反应器单元中包含2个厌氧池和3个好氧池,生化反应池中采用活性污泥ASM1模型来模拟整个生物化学反应过程,二沉池部分选用二次指数沉淀速率模型来模拟污水的沉淀过程.
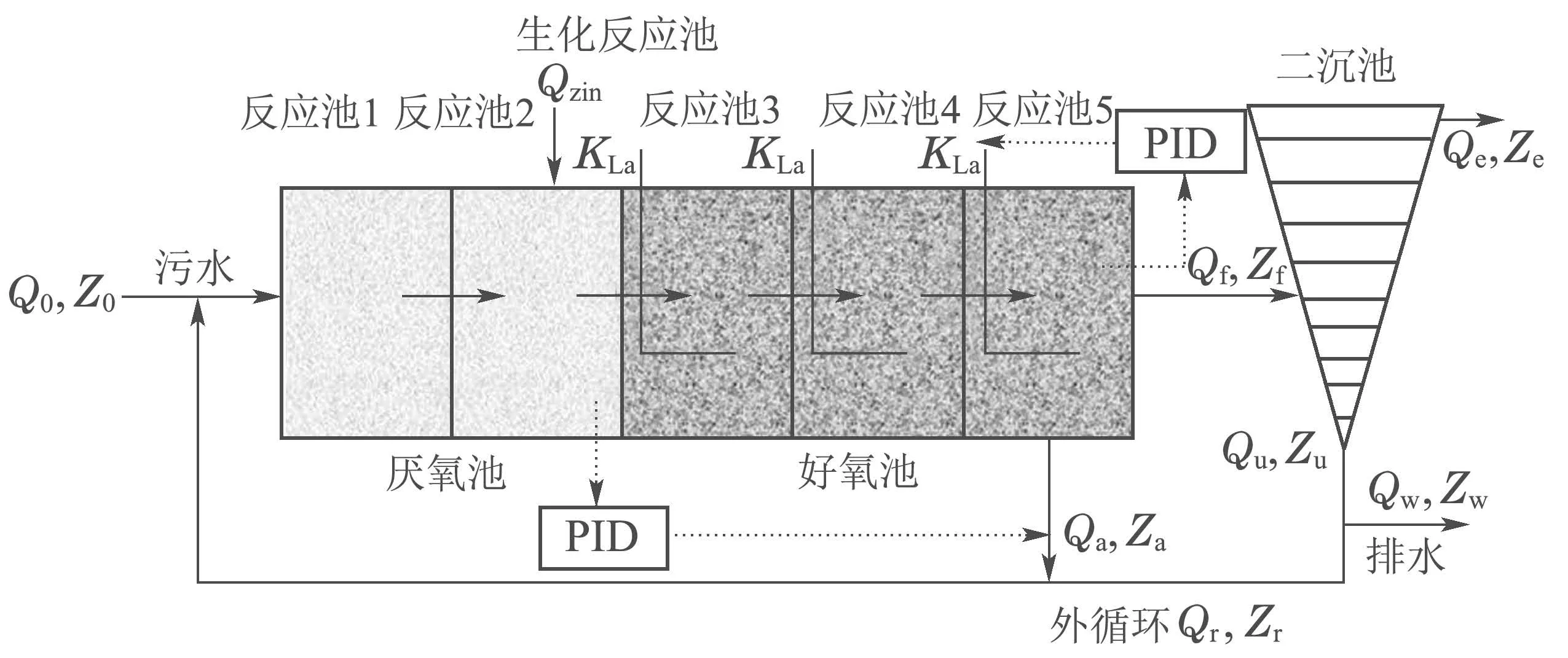
图1 BSM1模型Fig.1 The model of BSM1
生化反应池中第五单元的溶解氧浓度和第二单元硝态氮浓度是活性污泥法去除污水处理过程中最为重要的控制变量,在污水环境中影响处理过程好氧微生物对污水的处理效果,同时也是控制曝气能耗和泵送能耗大小的关键因素[20-21].因此对第五分区溶解氧浓度和第二分区硝态氮浓度的设定值进行优化设定,是提高污水处理过程在出水约束的条件下实现节能降耗优化性能的重要手段.
2.2 优化模型
在污水处理厂的污水处理过程中,系统能耗体现了在控制过程中由控制设备等一系列能耗总和.按照传统的控制方法,控制设备需进行长期高负荷的控制,才能够达到使出水水质达标的目的;如果系统能耗降低,意味着控制设备控制没有实现完全控制,可能导致出水水质的超标而造成罚款.由此可见,系统能耗和由出水水质超标而造成的罚款是一对相互矛盾的指标,需要对两个指标进行建模分析.主要的能耗成本包括曝气能耗和泵送能耗两方面,这两个能耗占总能耗的70%以上,所以定义能耗模型的优化问题为
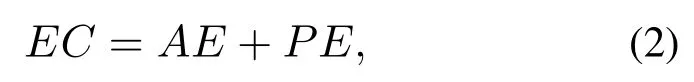
其中:EC表示能耗,AE表示曝气能耗,PE表示泵送能耗.根据污水处理过程中的反应变量及模型参数,AE和PE分别表示为[22]

其中:SO为溶解氧浓度;T为优化周期;V 为反应池的单元体积;KLai为氧气转换系数;Qa为内会流量,Qr为污泥回流量,Qw为污泥流量.
EQ表示向收纳水体排放污染物所需支付的费用,按基准定义如下式,其值越小,对应的处理费用越少.同时,EQ也是污水经处理后衡量出水水质的综合性指标,其值越小,说明出水水质也越好,相反,值越大,说明出水水质越差.
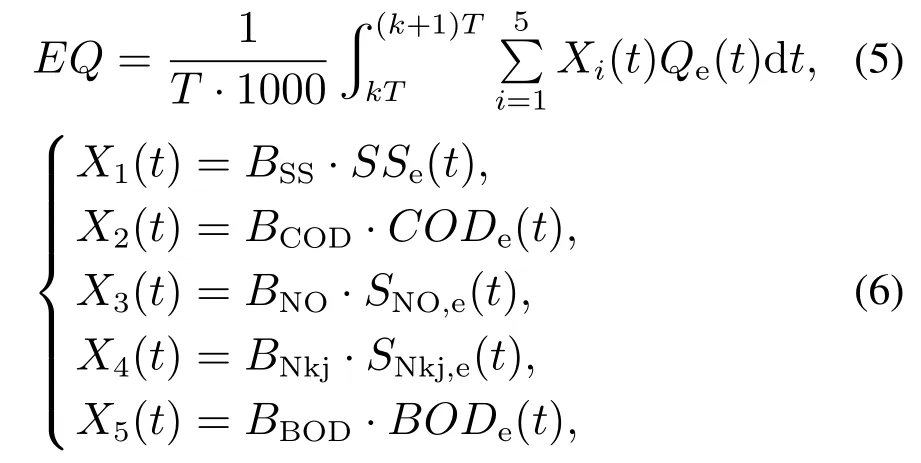
式中BSS,BCOD,BNO,BNkj,BBOD分别为出水悬浮物浓度、化学需氧量、硝态氮浓度、凯氏氮浓度、生化需氧量对EQ影响的权重因子.其中:BSS=2,BCOD=1, BNO=30, BNkj=20, BBOD=2.
本文针对污水处理过程的优化性能指标,通过改进的MOEA/D方法对EQ和EC进行优化.在活性污泥法的污水处理过程中需要进行各种化学以及生化反应,前置反硝化的处理工艺使得好氧区的溶解氧浓度强烈影响着缺氧区的硝态氮浓度,同时,缺氧区硝态氮又流经好氧区,因此污水处理过程控制变量间耦合严重,曝气能耗、泵送能耗、出水指标间存在着相互矛盾的多目标优化特性. EC与EQ指标是具有典型的冲突特性的性能指标,即,改善出水水质(EQ变小),必然需要能耗的增加(EC变大);反之,能量消耗降低(EC变小),也将引起出水水质的变差(EQ变大).因此,对于污水处理能耗与水质性能指标的优化问题本质上属于多目标优化问题.
对于整个污水处理过程,首先要确定性能指标与优化设定值间的优化关系.根据出水指标的限制值以及第五单元溶解氧浓度和第二单元硝态氮浓度在实际设定过程中的限制,令x1为溶解氧浓度的设定值,x2为硝态氮浓度的设定值,x=[x1,x2]为两个设定值组成的优化设定向量,fEQ,fEC分别为EQ与EC和优化向量间的函数表达,建立如下多目标优化模型:
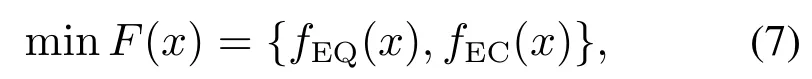
不等式约束为
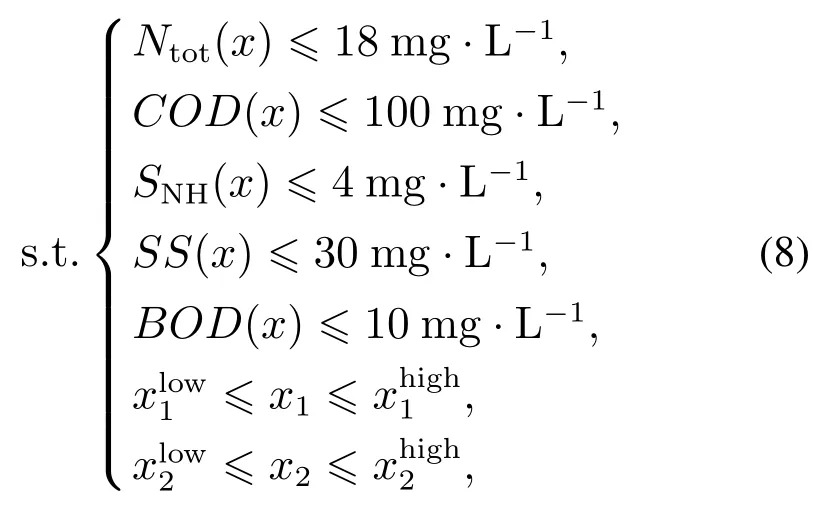
其中:Ntot为总氮浓度,SNH为氨氮浓度,和分别为溶解氧浓度和硝态氮浓度优化设定值的下限和上限.通过不等式约束以及EQ与EC与设定值建立的关系组成多目标最小化问题.
3 污水处理优化控制方法
3.1 MOEA/D算法
基于分解的多目标优化算法将多目标问题分解为N个标量的子问题.它通过进化出一代解的种群来同时解决所有的子问题,相邻子问题间的关联程度是由它们之间的聚合系数向量的距离进行定义的.最新种群是从所有代中选出每一个子问题的最优集合[13].
MOEA/D将求解帕累托前沿近似解的问题转化为一组标量优化问题时,采用的是切比雪夫聚合方法,其计算公式为
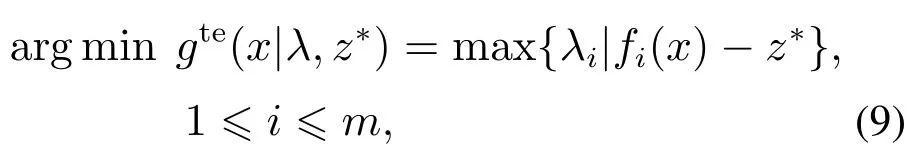
式中:m代表解的个数,λi为第i个权重向量,z∗表示参考向量.其含义是在每个子问题中,在其分配的参考向量下,找到相对于参考点来说下降最多的点,保证了每次迭代使种群能够向着帕累托前沿的方向进化.
基于分解的多目标进化算法虽然能够找到帕累托前沿,但是其寻优的速度以及最终求得的帕累托解的分布性需要提高.对于污水处理过程来说,能够以最短的进化次数找到多目标优化问题的解集,以及确保解集的分布性良好能够使的污水处理优化方案得到进一步提升.
3.2 SS-MOEA/D算法
对于一个多目标优化算法,评判其性能的优劣是通过其收敛性以及分布性来体现的.在MOEA/D算法中,寻找最优解的核心是通过交叉变异产生子个体,比较子个体与当前的所有个体的好坏,进行种群间的更替.由此可见,在基于分解的多目标进化算法的种群进化过程中,产生的子代与当前的种群邻居范围内进行比较的过程显得尤为重要.
对于第i个子问题,在它的邻域范围内随机找出两个个体作为父代进行交叉变异产生一个子代,然后通过比较第i个子问题邻域内的解与新解的切比雪夫值的大小来进行解的更新.但是其中有以下问题:通过交叉变异产生的子代个体可能并不适合当前的子问题i,可能更适合子问题j.在每一次的新解替换旧解的过程中,若只在第i个子问题中进行新旧解的更替,在一定程度上弱化新解的替换能力,使得每一次解的进化不够完全,从而降低了算法的寻优速度.
为了解决这一问题,本文中定义了一种新个体与子问题间的关系,从N个子问题中找到与新个体关系最为紧密的子问题,其关系式定义如下:
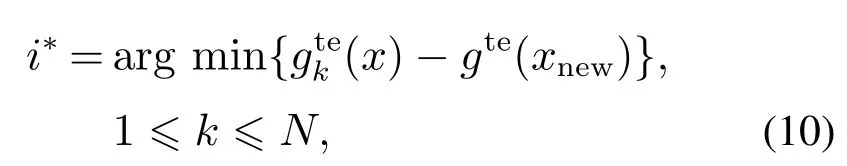
将新解在第i∗个子问题以及产生新解的子问题的邻居范围内进行新旧解的更替,相比于只在产生新解的子问题中进行新旧解更替的优势在于首先提高了新解的利用效率,进一步提升了算法的寻优速度;其次增加了种群的多样性,防止算法陷入局部最优.
图2中展示的是改进MOEA/D算法新解找到合适的子问题的二次寻优图.对于两个目标函数来说,通过两个目标函数值建立目标空间,其中:z∗表示参考点,λ表示权重向量,xnew表示通过遗传变异得到的新解,fit表示每个个体在目标空间对应的目标函数值.由图2中可以看出,当父代进行交叉变异操作后产生的子代个体,通过计算个体与子问题的切比雪夫关系,得到最适合的子问题后,新解所替换的范围变大,这样对种群整体的进化速度有明显的提升,同时,新解在不同的子问题中作为父代产生子代时,在一定程度上增加了子问题中解的多样性,避免最终陷入局部最优,从而更好的完成优化算法进行寻优的过程.
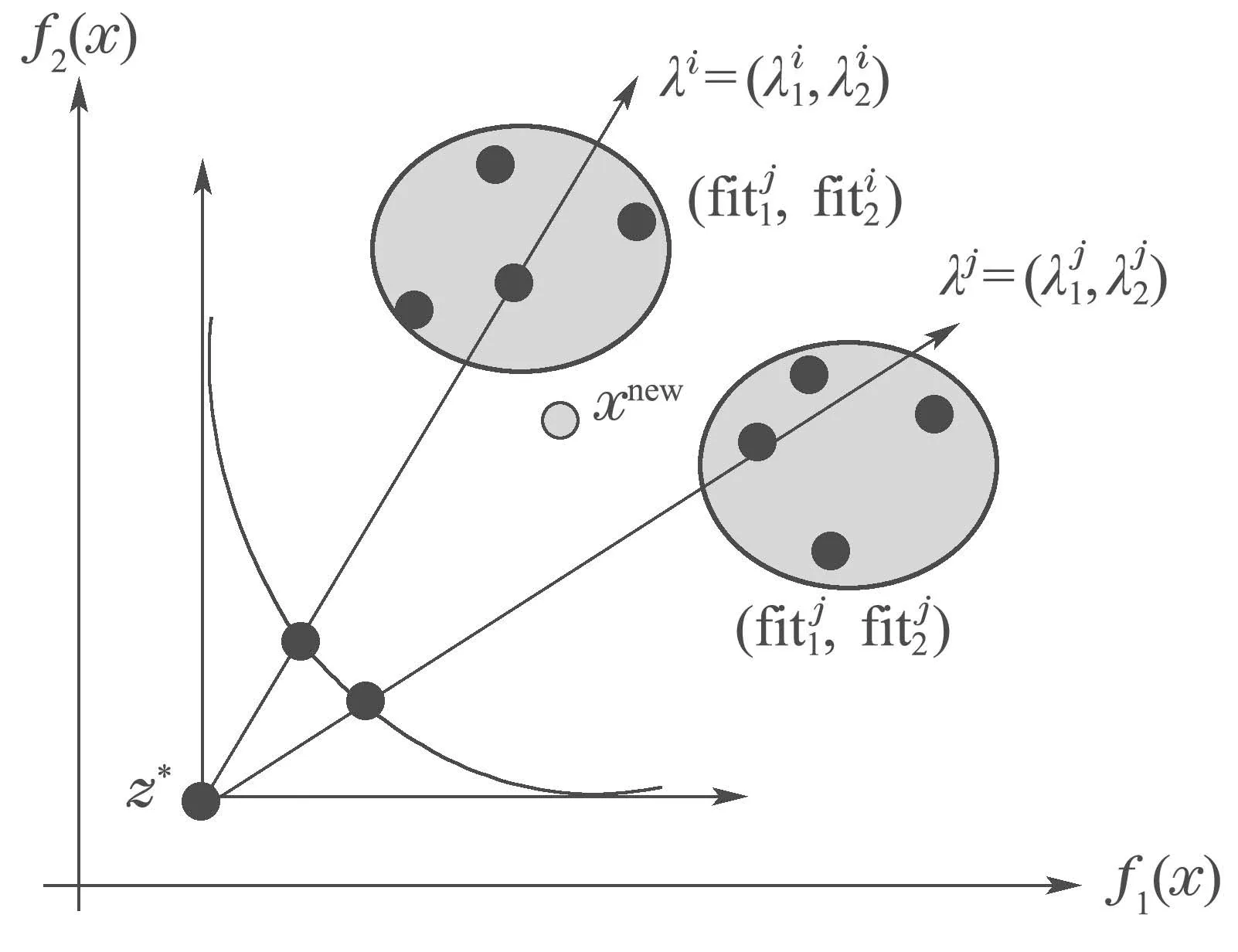
图2 二次寻优图Fig.2 Secondary search figure
改进的SS-MOEA/D算法输入的输入为多目标优化问题和算法终止条件;算法的输出为最优解{x1,···,xN}与相对应目标问题的函数值{f(x1),···,f(xN)}.以下为整个SS-MOEA/D算法的流程:
步骤1初始化:在可行性空间进行如下操作:
1)均匀产生初始种群x1,···,xN以及产生均匀分布的N个权重向量:λ1,···,λN;对参考点z∗进行初始化,令=min fi(x1),···,fi(xN);初始化邻域内个体集B(i),设置EP为空;N为算法定义的种群规模,也是子问题规模;
2)计算任意两个权重向量间的欧式距离,找出每个权重向量最近的T个权重向量;T为邻域规模.
步骤2更新:对每个i=1,···,N操作如下:
1)基因重组:从B(i)中随机选取两个序号k和l,用遗传算子由xk和xl产生一个新的解y;
2)改进:对y进行修复和改进产生y′;
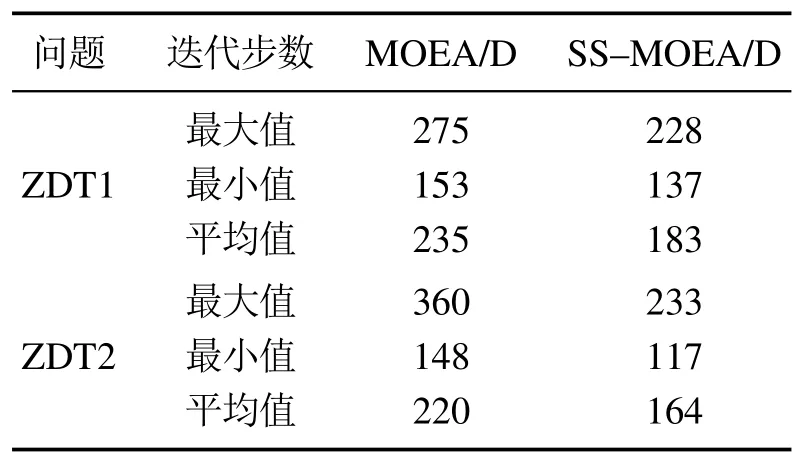
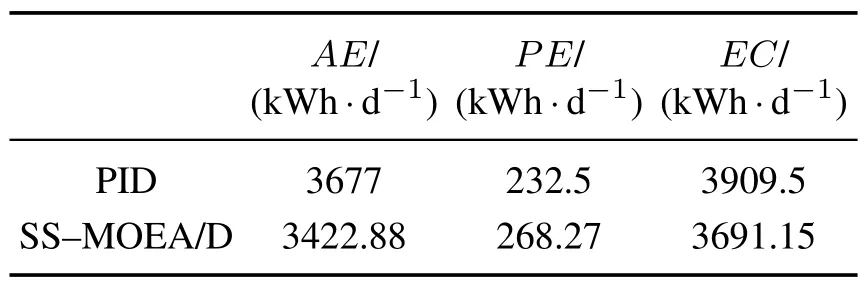
3)更新z∗:从j=1,···,m,如果 4)更新邻域解:通过计算得到新产生的解的最适合的子问题i∗,i∗=arg min(x)−gte(xnew);对于在邻域B(i∗)和邻域B(i)中的每一个解xj,如果gte(y′|λj,z)≥gte(xj|λj,z),则令xj=y′. 5)更新EP:从EP中移除所有被F(y′)支配的向量,如果EP中的向量都不支配F(y′),将F(y′)加入EP. 步骤3判断终止条件:停止并输出EP,如不满足条件转到步骤2. 在多目标优化问题中,多目标优化算法解决的是多个目标同时达到最优的问题,所求得的解在多目标优化问题中被认为是等地位的.但对于污水处理过程中,通过SS-MOEA/D算法求得的解集中所有的解都满足约束条件,即所有解都满足出水水质指标.当选择由SS-MOEA/D算法计算得到的帕累托最优解集中的任意一个解作为溶解氧和硝态氮控制器的跟踪设定值时,污水处理最终得到的水质均符合排放标准.所以考虑到所有解集都满足约束条件下,从帕累托解集中找到当前最满意的设定值时,本文中采用的是比较每个解对当前时刻系统的能耗的大小,选择使能耗最低的解即为当前最满意的优化设定值,根据这种方法找到的优化设定值既满足了出水水质的要求,又使得系统的能耗最低. 在建立好的污水处理优化模型中加入SS-MOEA/D优化算法后,所得到的是针对污水处理过程中EC和EQ优化问题的一组帕累托最优解.在这些解中,需要找到当前状态下的一组满意优化解作为控制器的跟踪设定值. 整个污水处理过程优化控制框架如图3所示. 图3 优化控制框架Fig.3 Optimized control framework 在该框架中展示了整个污水处理过程的优化控制系统:首先通过优化模型对污水处理过程中的能耗和出水水质与溶解氧和硝态氮浓度设定值之间建立的函数关系,构造污水处理过程多目标优化模型;然后针对建立好的多目标优化问题,通过SS-MOEA/D算法求得帕累托最优解,并从中选择出当前时刻最满意的解作为溶解氧浓度和硝态氮浓度的优化设定值;最后多变量控制器通过污水处理过程中溶解氧和硝态氮的真实值与优化设定值的差值,对其进行跟踪控制.本文中所采用的控制器是PID控制器,通过调整第五分区溶解氧转换系数(KLa5)控制污水中的溶解氧浓度,调整内回流量(Qa)控制硝态氮的浓度. ZDT(1,2,3,4,6)系列问题是为了测试多目标优化算法优劣而提出的一系列多目标优化问题,其中包含了帕累托前沿连续、不连续的情况,是公认测试优化算法性能的优化问题.逆代距(inverted generational distance,IGD)指标是评判多目标优化算法的重要指标,其计算公式如下[14]: 式中:P∗为真实帕累托前沿,P为优化算法求得的前沿.该指标能够同时体现出优化算法的多样性及收敛性.值越小说明得到的帕累托前沿与真实的帕累托前沿越接近,分布越好;相反,其值越大说明得到的帕累托前沿越偏离真实前沿,分布性越差. 为了比较出本文提出的SS-MOEA/D算法在寻优步数上有所提升,设计如下实验:针对ZDT系列的1,2问题,使优化算法进行迭代优化,停止条件是达到固定的IGD值(IGD<0.6·10−3),比较算法的迭代步数,程序运行20次.MOEA/D算法和改进的SS-MOEA/D算法的比较结果如表1所示.由表中可以看出在对于ZDT1和ZDT2的问题中,改进的SS-MOEA/D算法在20次的实验中达到相同IGD值所需的迭代步数的最大值、最小值以及平均值均少于MOEA/D算法,证明改进的SS-MOEA/D 能够用更少的寻优步数找到帕累托前沿. 表1 迭代步数对比Table 1 Comparison of IGD indicators 为了比较本文提出的SS-MOEA/D算法的性能,设计的实验如下:对ZDT系列的1,2,3,4,6问题,使算法迭代300次,计算IGD指标,程序运行20次,取平均值并进行排序.比较结果如表2所示. 表2 IGD指标对比Table 2 Comparison of IGD indicators 如表2所示,SS-MOEA/D在解决ZDT问题时,能在多数的多目标问题中表现突出,尤其在ZDT(2,6)中结果明显优于其它算法;对于ZDT3,本文中的优化方法尽管表现不是最优,但与最优算法结果相差不大.综合所有ZDT问题的结果,证明算法在解决帕累托前沿连续、不连续的优化问题中的有效性,并在收敛性与多样性上所提升. 针对污水处理过程中能耗与出水水质间的优化问题,对本文提出的优化方法进行测试.本实验的研究是基于国际仿基准测试平台BSM1模型,采用晴天天气下的污水流量和组分变化来仿真模拟真实污水处理厂的实际运转工况,采样间隔为15 min,仿真时间为7 d,优化周期为2 h.SS-MOEA/D 算法参数设置与PID控制器参数设置如表4所示. 表3 参数设置Table 3 Parameters setting 将多目标优化方法在BSM1仿基准模型中进行优化,第五分区溶解氧浓度和第二分区硝态氮浓度的设定值会随着污水环境不断改变.图4和图5是溶解氧和硝态氮的优化过程跟踪控制曲线. 由图4可以看出,SO优化设定值可以根据污水处理过程中系统运行的实时状况不断调整,PID控制器能够以较高的控制精度对SO优化设定值进行跟踪.体现出了优化算法能够对污水处理过程中的溶解氧设定值进行实时优化. 图4 SO跟踪控制图Fig.4 Tracking control effects of SO 图5 SNO跟踪控制图Fig.5 Tracking control effects of SNO 表4 平均出水水质对比Table 4 Comparison of average effluent water quality 图5展示了SNO优化设定值的变化过程,由图中可以看出系统能够根据优化问题对硝态氮的浓度设定值进行实时改变. 为了体现优化策略污水处理过程中对EC和EQ的优化效果,在相同条件下进行PIDx闭环控制,SNO分别设置在2 mg/L和1 mg/L.表4给出了PID闭环控制以及SS-MOEA/D优化控制方法在7天内的平均出水数值的对比.由表中可知,经过SS-MOEA/D优化算法得到的平均水质均符合排放标准. 表5中的数据表明在加入优化算法与直接控制对污水处理过程系统能耗的比较.相比于PID闭环控制,基于SS-MOEA/D优化控制方法的AE减少了6.91%,PE增加了1.54%,EC降低了5.58%.实验结果证明所提出的基于SS-MOEA/D优化控制方法在污水处理过程中的有效性. 表5 能耗对比Table 5 Comparison of energy consumption 与单目标优化问题不同,多目标优化问题无法进行简单搜索比较出当前解中的优秀个体.为了找出使污水处理过程中使能耗与出水水质同时达到最优的解,本文提出了一种基于改进的MOEA/D优化控制方法.通过理论分析与仿真实验得到以下结论:1)针对MOEA/D算法每一次产生的新解,从所有子问题中找到最合适新解的子问题,并在其邻域范围内进行种群的更替,在原本的子问题的基础上进行二次寻优,提高子代利用率,在相同的迭代次数下,针对ZDT系列优化问题,能够快速收敛到帕累托前沿上,并提高了解的多样性.2)针对污水处理过程优化问题,本方法通过在BSM1仿基准平台上优化SO与SNO的设定值,达到了同时优化出水水质以及能耗的目标,用较少的能耗达到了污水排放的要求,有效的减少了污水处理过程的成本.3.3 污水处理优化控制过程
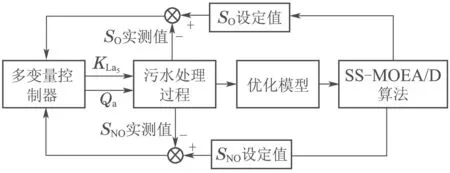
4 仿真实验
4.1 ZDT优化问题
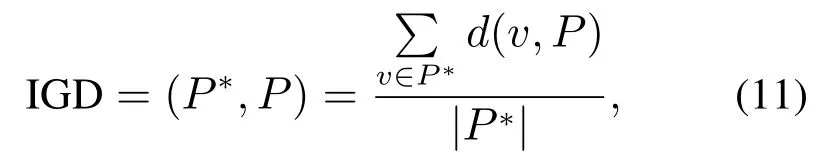
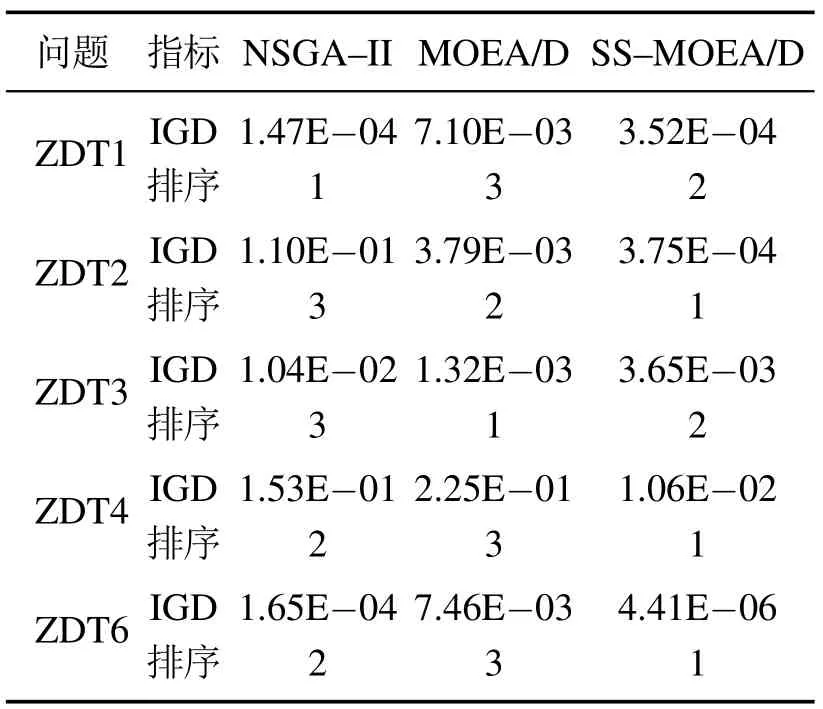
4.2 污水处理优化仿真实验

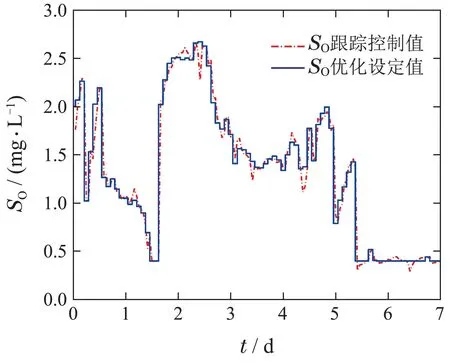
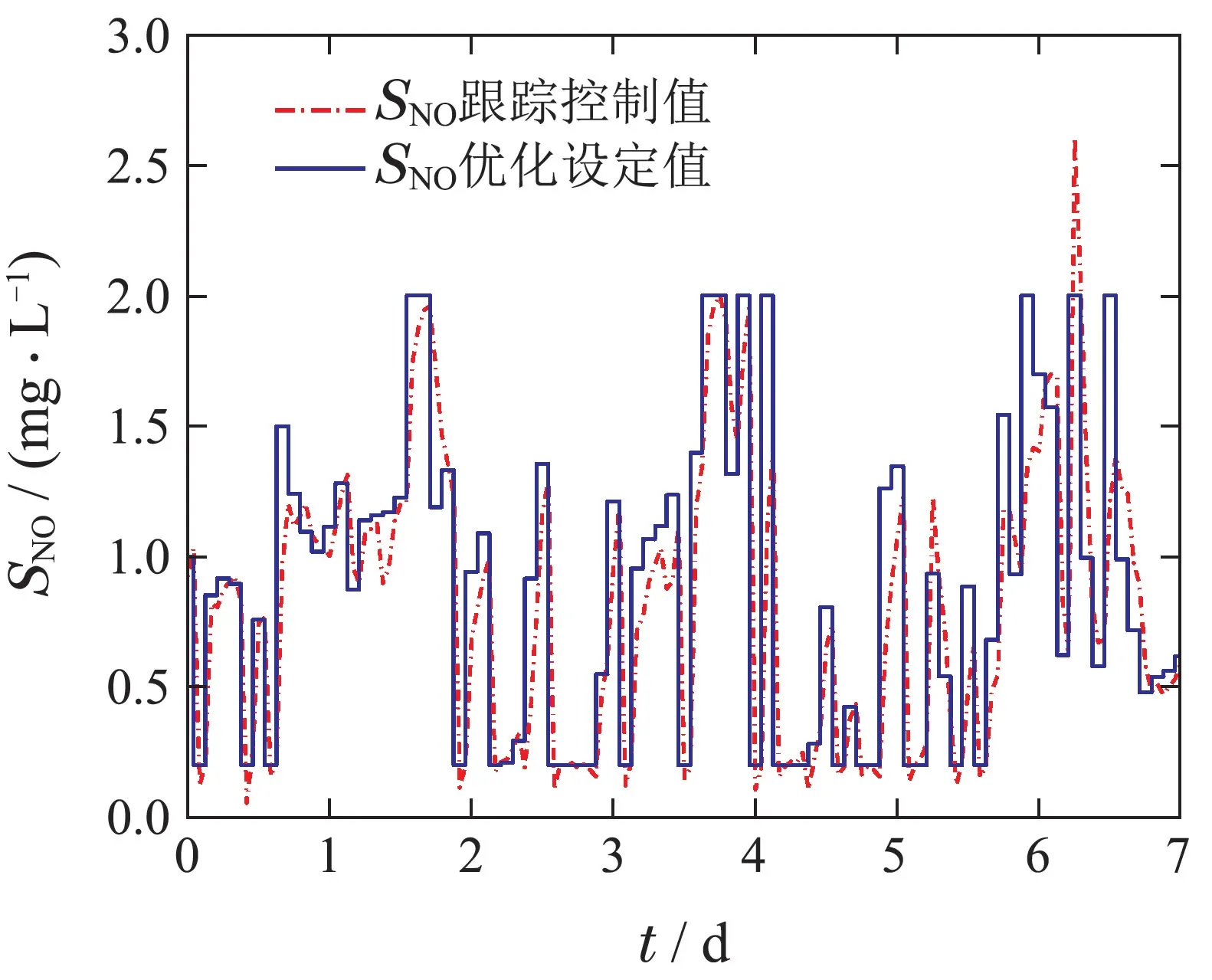
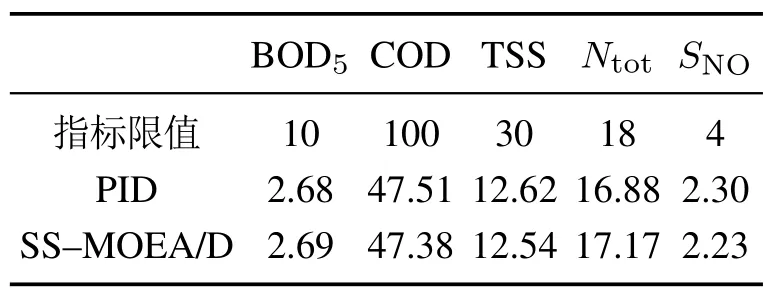
5 结论

