含攻击角约束的网络化弹药分布式模糊协同制导律

姜 尚,田福庆,孙世岩,梁伟阁

(海军工程大学兵器工程学院,湖北武汉 430033)

1 引言

近年来,我海军为适应高新技术条件下的国际热点地区局部战争,提出了“前沿作战,从海到陆,由海制陆”、“垂直包围”、“超视距登陆”等海军战略战术,对舰炮武器提出了更高的要求:对海对岸具有持续火力支援能力与精确打击能力[1].舰炮仅是弹药的载体与发射系统,在对战场的有效性方面,至关重要的是弹药的终点效应,应用新技术可以达到更好的作战效果,借助舰炮平台发射的舰炮制导弹药应运而生.

重要军事目标配备的多层防御体系日臻完善,依靠单枚弹药突防日益困难,将多枚制导弹药组网,协同进行饱和攻击或分批次完成“侦查-打击”任务是一种更加符合现代信息化战争思想的作战方法,突破依托战前预置的战役级协同作战,采用灵活高效的武器级协同控制手段,借助通信链路组织多枚大口径舰炮制导炮弹构成网络化弹药,在有限时间内,作战单元通过共享信息协同命中时间,并以各自期望的攻击角完成对近岸机动目标的精确打击任务,将能有效地提高海上火力支援与突防能力[2].

用以实施多弹协同的末制导律正逐渐成为研究多智能体协同控制中的热点课题[3].按作战单元间是否存在信息共享,可将其分为闭环式与开环式,虚拟领弹[4]、偏置比例[5]、滑模控制[6]、动态面控制[7]等方法已成功应用于后者,但它需要在发射前预设导引时间,在末制导过程中弹药间并没有信息交互,不能实现真正意义上的协同[8].闭环式的通信拓扑结构包括集中式[9-10]与分布式[11-14,16-17],张春妍等[9]针对静止目标,根据各导弹的剩余攻击时间之差对偏置比例导引律中的比例系数进行调节,设计得到了同时满足命中落角和攻击时间约束的协同偏置比例导引律,进而Zhao等[10]在传统比例导引算法的基础上,提出了多导弹齐射攻击的协同策略,可对机动目标进行攻击,然而集中式存在鲁棒性差、通信代价高等缺陷[11].

实战中难以保证集中式通信链路畅通,故常采用分布式拓扑,作战单元只与相邻单元进行信息共享,通过图论中Laplacian矩阵描述网络化弹药的通信关系.针对静止目标,Wang等[12]以剩余时间为协调变量,设计了可实现落角约束的协同偏置比例导引律,并改善了可能存在的过载超限、抖振等问题,Cho等[13]为避免制导指令的奇异性,引入正连续非线性函数,使Lyapunov稳定性为负半定的,提出了一种滑模制导律.针对机动目标,现有文献对其加速度的处理方法可分为两类:1)视目标切向、法向加速度(若无特别说明,切向、法向指在速度的切向与法向)均为未知的有界扰动量,孙雪娇等[14]运用网络同步原理设计了一种多导弹拦截的分布式增广比例协同导引律,具有通信量小、可扩展性强等特点,但由于目标加速度难以测得,对导弹的设计提出了很高的要求;2)视目标切向加速度为未知的有界扰动量,运用扩张状态观测器(extended state observer,ESO)估计法向加速度,ESO由韩京清[15]首次提出,在没有对象精确模型的情况下能同时估计系统的内部状态与外部干扰,宋俊红[16]、吕腾等[17]提出了带有攻击角约束的协同制导律,基于图论运用有限时间一致性理论设计视线方向上的控制指令,并利用ESO估计目标法向加速度,采用滑模设计视线法向控制指令,但弹目接近时控制指令易产生终点发散与抖振现象,主要因素如下:1)未合适地处理目标切向加速度;2)滑模控制存在变结构项,现多采用连续饱和函数近似代替变结构项,由于切换增益难以确定,效果不尽如人意,为此,商巍等[18]设计了综合视线角速率以及弹目距离的自适应模糊系统逼近变结构项,有效削弱了制导过程中的抖振;3)为使滑模快速趋于滑膜面,采用包含弹目距离的单一自适应趋近律.

相较于导弹,大口径舰炮制导炮弹有其特殊性,尤其体现在控制能力方面,多导弹相关研究成果并不能直接应用,需要优化改善上述影响制导性能的因素.现有文献对攻击角的定义主要有3种[19]:炮弹航迹落角、弹目视线角、弹目碰撞时两者速度矢量的夹角,然而,上述文献均适用于前两种可转化为固定视线角约束的特殊情况,为保证研究具有较好的普适性,本文选用后者,通过零化弹目相对法向速度,可将攻击角约束转化为时变的视线角约束.

综合考虑上述因素,本文提出了一种含攻击角约束的有限时间分布式模糊协同制导律,通过有限时间稳定性理论与Lyapunov第二法证明了命中时刻能在有限时间内趋于一致,同时,全系统状态具有一致最终有界性与有限时间收敛性,主要创新点如下:1)在视线方向与视线法向上设计双ESO,精确快速地观测机动目标的切向、法向加速度,并分析含观测误差的系统稳定性;2)以积分滑模与非奇异终端滑模作为输入量,设计模糊自适应逼近器,补偿系统的不确定干扰,有效削弱了控制指令抖振;3)在视线法向,结合弹目距离设计两阶段滑模自适应趋近律,较好地改善了控制指令终点发散现象.

2 模型建立

2.1 网络化弹药-目标相对运动模型

建立纵平面网络化弹药-目标相对运动模型,如图1所示,Pi(i=1,···,h)与T分别表示第i枚制导炮弹与目标,Ri为弹目距离,qi为视线角,vPi,aPvi,aP⊥i,θPi,ηPi与vT,aTv,aT⊥,θT,ηTi分别为Pi,T的速度、切向加速度、法向加速度、航向角、速度倾角.

图1 网络化弹药-目标相对运动Fig.1 Relative motion of networked munition and target

为便于分析讨论,做合理假设如下:

假设1将Pi,T视为质点,并且变量Ri,qi,θPi,θT通过现有技术手段容易测得,vPi可控,且始终满足vPi>vT.

弹目相对运动方程可由式(1)-(3)表示:

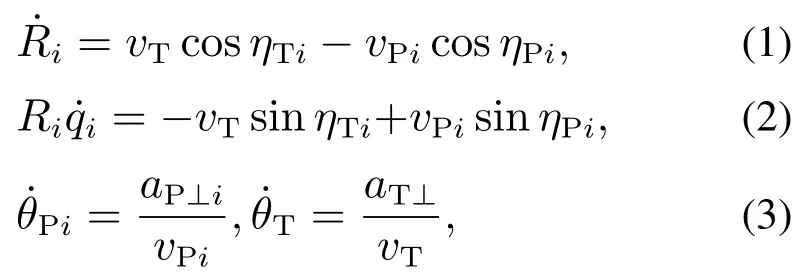
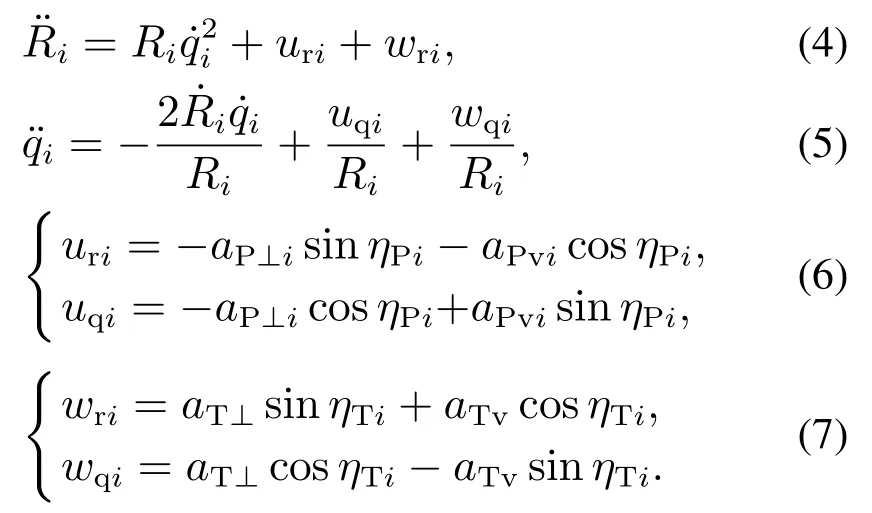
2.2 近岸机动目标模型

近岸机动目标由一阶惯性环节描述

式中:τT为时间常数;为切向、法向加速度指令,做合理假设如下:

假设2aTv,aT⊥,有界,且

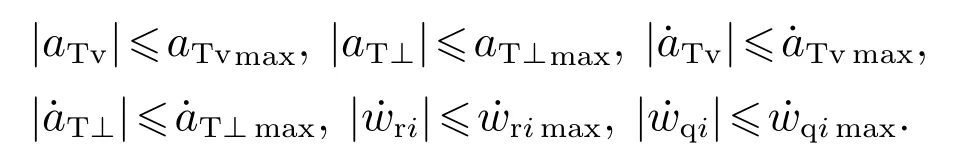
2.3 攻击角模型

攻击角为命中时刻Pi,T速度矢量夹角,如图2所示.

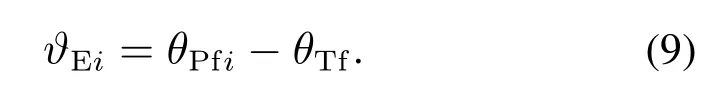
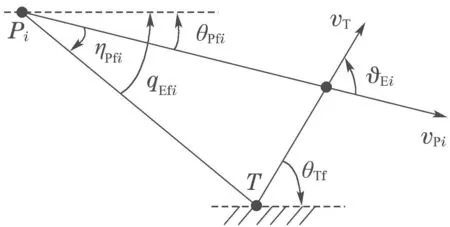
图2 碰撞航线攻击角Fig.2 Impact angle of collision course

碰撞航线上弹目相对法向速度为零.

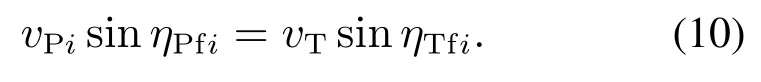
联立式(3)(9)-(10)可知,对于给定的ϑEi,存在唯一的期望视线角qEfi与之对应

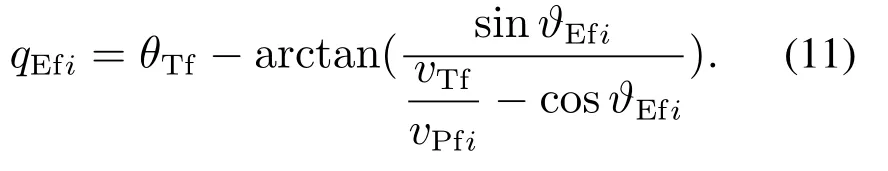
由此,攻击角约束转换为时变视线角约束,为使Pi平稳地以qEfi命中T,令式(11)不仅在终点成立,而是从末制导初始就成立,其1,2阶导数分别为

2.4 系统状态空间

令tgoi为Pi的剩余飞行时间,其命中时刻为tfi=t+tgoi,对邻弹有tfi−tfj=tgoi−tgoj,若控制tgoi在有限时间内趋于一致,并且qi同时满足qEi约束,即网络化弹药实现了含攻击角约束的的协同攻击任务.可采用估计tgoi,因此,定义系统状态变量为

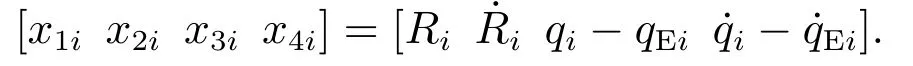
联立式(1)-(7),可得网络化弹药协同末制导的系统状态空间为.

基于前述,设计协同制导律的目的:设计双ESO估计wri,wqi,设计uri使x1i,x2i各自于有限时间内趋于一致,设计uqi使x3i,x4i各自于有限时间内趋于零,设计模糊自适应逼近器补偿系统的不确定干扰.

2.5 双ESO模型

定义观测变量[z1iz2iz3iz4i]=,在视线方向构建第1个ESO:

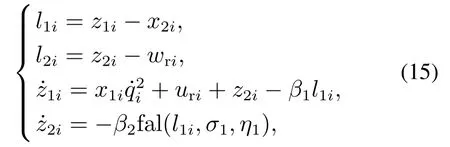
式中:0<βi,i=1,2,非线性增益函数fal为

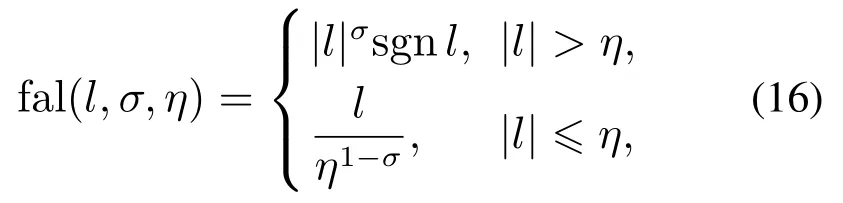
式中:0<σ <1,0<η,对l1i,l2i求导:

定义变量dri为系统在视线方向上受到的干扰,并令dri=l2i,当ESO(15)处于稳态时其稳态误差为

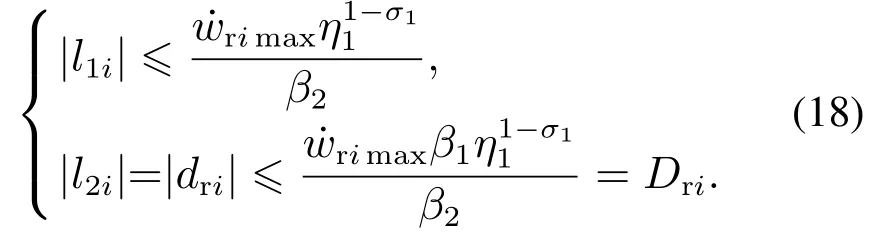
在视线法向构建第2个ESO:

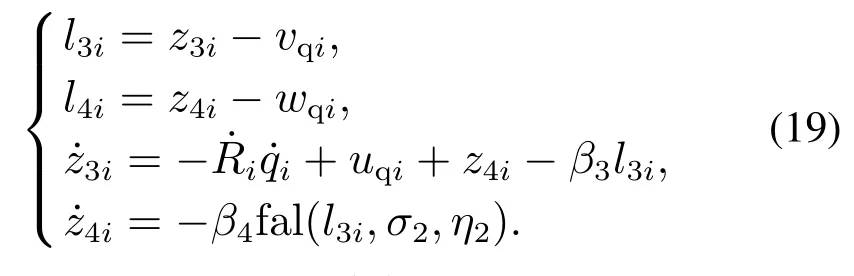
同理可得ESO(19)稳态误差为

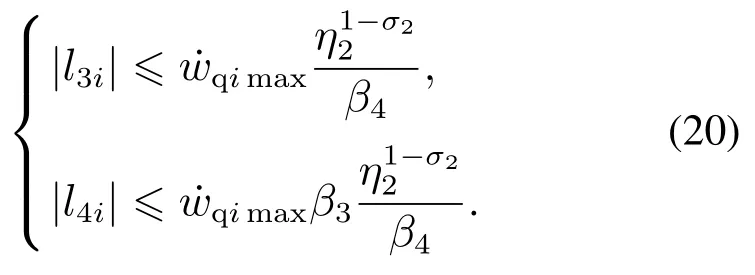
由式(18)(20)可知,无论被观测量是否连续,通过选择合适的参数,并令β2,β4足够大于β1,β3,所设计的双ESO模型就可以进行精确的观测,即z1i→x2i,z2i→wri,z3i→vqi,z4i→wqi.

3 末制导律设计

3.1 视线方向控制指令设计

在网络化弹药协同末制导的过程中,弹药通过拓扑通信网路进行信息交互获得其它弹药状态信息,以达成多弹协同,这种信息交互可以通过图论来描述.本文用无向连通图G=(P,ζ,A)描述网络化弹药间的通信拓扑关系,其中:P 为网络化弹药节点Pi的集合;ζ表示节点Pi间的连线;图G中的任意边可表示为(bi,bj),A=[aij]∈Rh×h为权系数矩阵.若Pi与Pj存在信息共享则(bi,bj)∈ζ,aij=1,否则(bi,bj)/∈ζ,aij=0,需注意aii=0.由于G是无向的,有aij=aji.若G中任意两节点间都存在至少一条通路,则G是连通的.

定理1针对系统(14)的视线方向子系统,当其通信拓扑图G保持无向连通时,采用ESO(15)并使用积分滑模设计视线方向控制指令如下,能使x1i,x2i各自于有限时间内趋于一致:

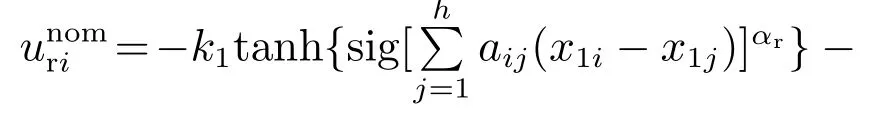
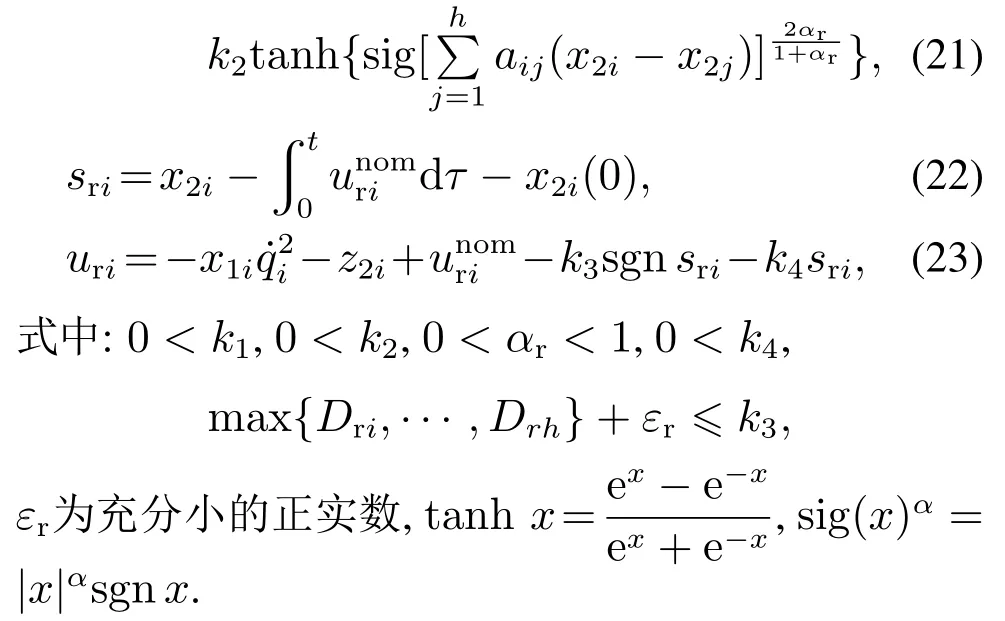
现对定理1进行证明,为保证积分滑模在趋近过程中有良好的动态品质,选取自适应指数趋近律为

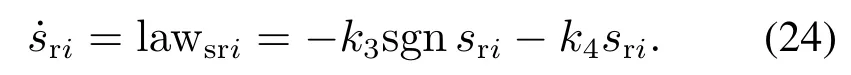
对式(22)求导,并结合式(21)(23)-(24)得

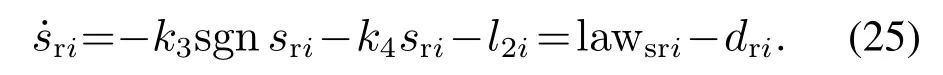
选取Lyapunov函数Vri=,求导得

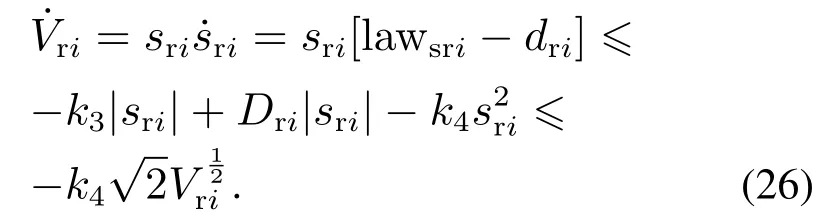
引理1考虑如下系统[20]:

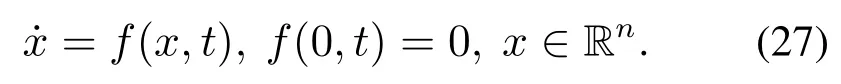
假定存在一个定义在原点邻域上的连续可微正定函数V(x),存在实数c>0,α∈(0,1)使(x)≥−cVα(x),则系统(27)的原点是有限时间稳定的,且稳定时间满足Tr≥.

由引理1可知,积分滑膜sri可在有限时间Tri内收敛至0,取Tr=max{Tr1,···,Trh},则有

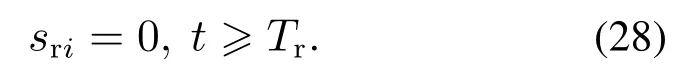
对式(28)求导,并结合式(21)-(23)可得

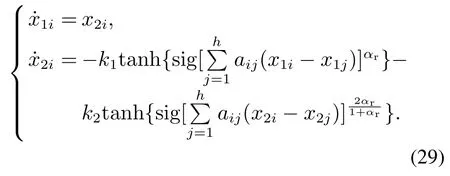
为便于定理1的分析与证明,给出有关二阶多智能体有限时间一致性收敛的引理:

引理2考虑如下二阶多智能体系统[21]:

式中:i=1,···,N,qi∈Rn,pi∈Rn,ui∈Rn为智能体i的位移、速度与控制输入,当其通信拓扑结构图G无向连通时,采用控制输入为

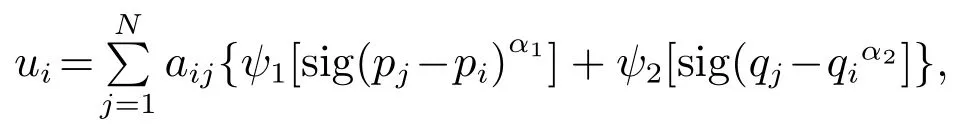
式中:ψ1,ψ2是连续的奇函数,并且参数满足0<α1<1,α2=,那么在上述控制输入的作用下,系统状态qi,pi能各自达到有限时间一致性收敛,即在有限时间内qi→qj,pi→pj,∀i,j=1,···,N.

根据引理2,可知对于系统(14),状态变量x1i,x2i能在有限时间内趋于一致,定理1证毕.

3.2 视线法向控制指令设计

在网络化弹药协同末制导的过程中,在视线法向为避免终端滑模奇异,选用一种非奇异终端滑模

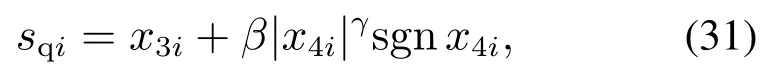
式中:0<β,1<γ <2,求导并结合式(14)得

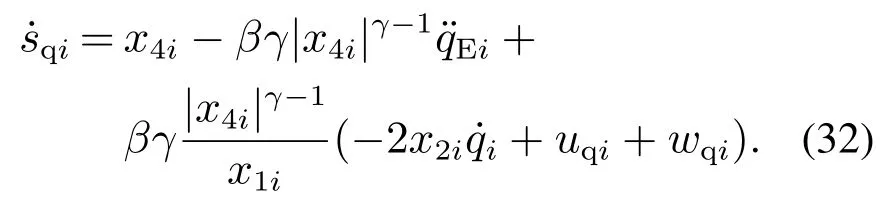
选取滑模自适应趋近律

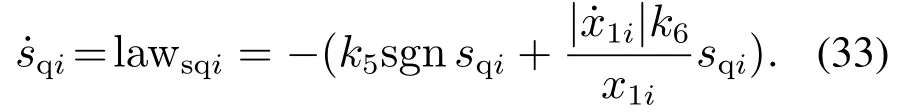
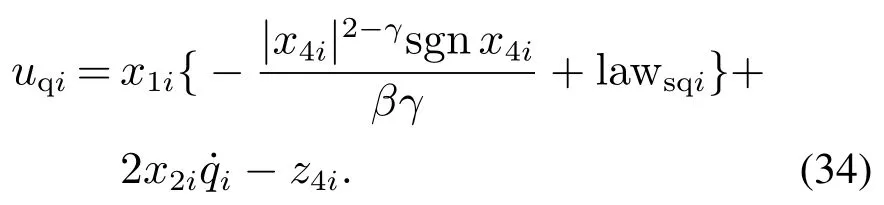
定理2针对系统(14)的视线法向子系统,采用ESO(19)与视线法向控制指令(34),系统状态变量x3i,x4i将在有限时间内收敛至0.

现对定理2进行证明,选取Lyapunov函数Vqi=,求导化简

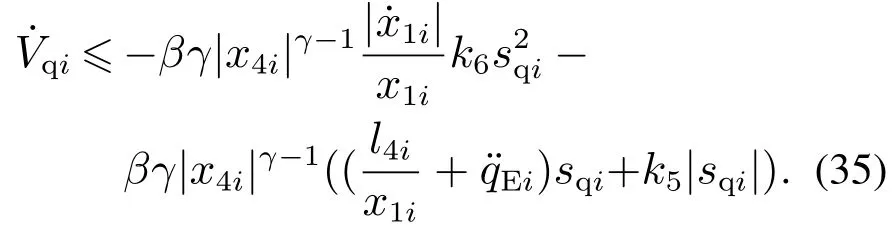
定义变量dqi系统在视线法向上受到的干扰,令dqi,由前述可知,其有界且满足|dqi|≥Dqi,取max{Dq1,···,Dqh}+εq≥k5,εq为充分小的正实数,则有

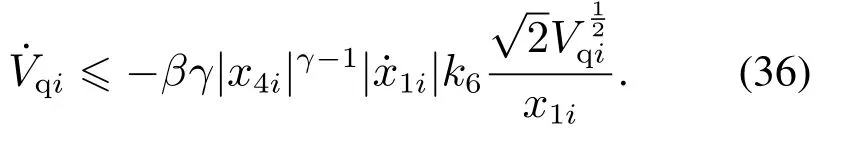
由引理1可知,非奇异终端滑膜sqi可在有限时间Tqi内收敛至0,取Tq=max{Tq1,···,Tqh},即有

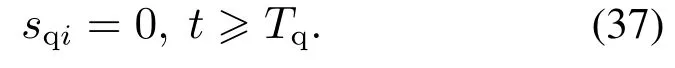
联立式(31)(37)进行分析可得

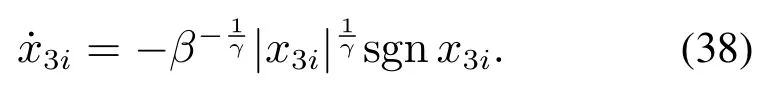
选取Lyapunov函数Vx3i=,求导得

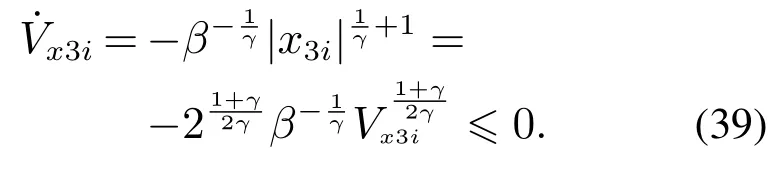
根据引理1可知,系统状态变量x3i,x4i能在有限时间内收敛至0,定理2证毕.

为使制导律连续,常采用含消颤因子的连续饱和函数sat(x)=代替变结构项sgn x[17],0<δ,此时uri,uqi为

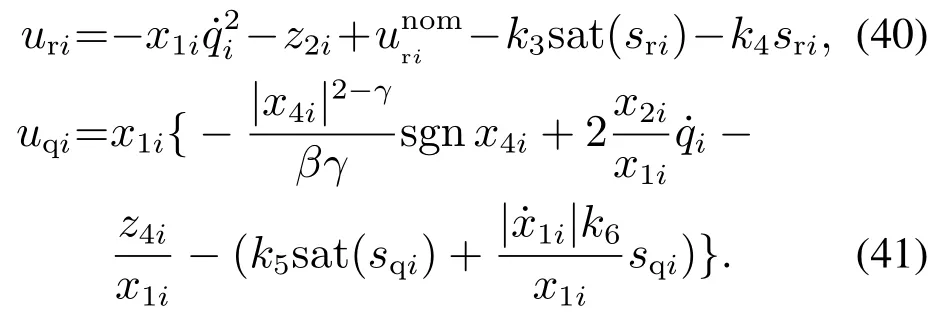
3.3 模糊自适应逼近器

目标机动导致k3,k5难以确定,取值偏小则难以满足稳定条件,取值偏大则会产生较严重的抖振,故设计模糊自适应逼近器,以削弱控制指令抖振.

模糊自适应逼近器Ξij(si|κij)(i=1,···,h; j=3,5)采用乘积推理机、单值模糊器和中心解模糊器,其本质上是从Ω ⊆R2到Y ⊆R的映射,第m条规则为

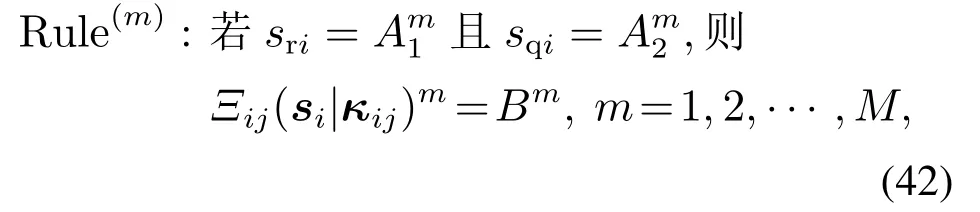
式中:si=[srisqi]T∈Ω为模糊自适应逼近器的输入量;输出量Ξij(si|κij)∈Y 为

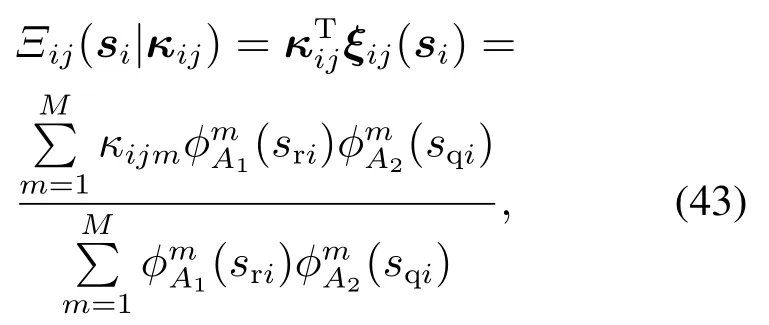
式中:κij=[κij1··· κijM]T为M维的自适应模糊参数向量,(x)为输入量的模糊隶属度函数,ξij(si)=[ξij1(si)··· ξijM(si)]T为M维的模糊基向量.

引理3函数Γ为定义在紧集Ω ⊆Rn上的实函数,∀ε>0,则一定存在由式(42)-(43)所建立的模糊自适应逼近器[23],使|Γ−κTξ(s)|≥ε成立.

定义最优逼近向量为

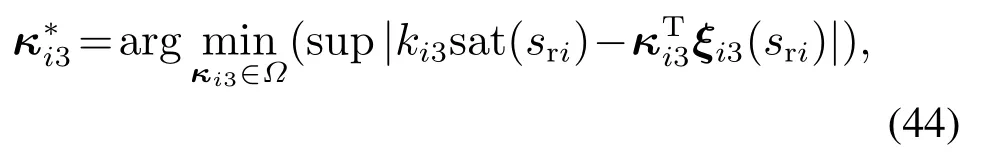
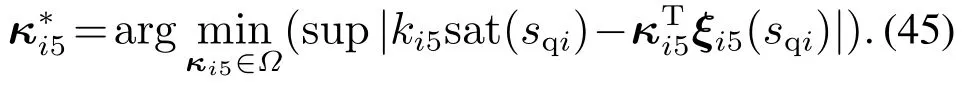
由引理3可知,对给定的任意小正常数εr,εq有如下不等式成立:

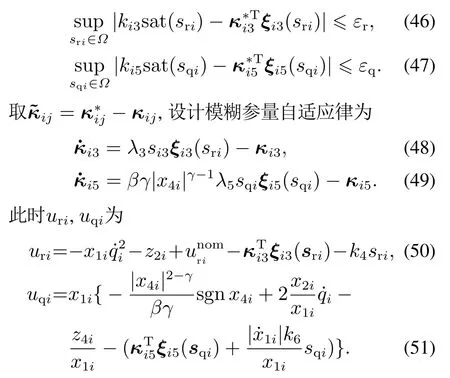
4 系统稳定性分析

引理4如果有常数10,对于任意两个维度相同的向量a,b 来说,有不等式(52)恒成立:

式(52)在p=q=2且ε=1的情况下,简化成

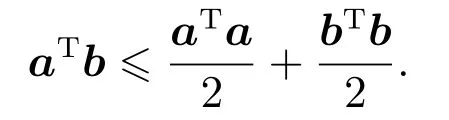
定理3对于系统(14),采用双ESO式(15)(19),模糊参数向量的自适应律如式(48)-(49),末制导律采用式(50)-(51),并选择合适参数,则全系统Lyaounov函数V 与滑模面sri,sqi一致最终有界,且在有限时间内x1i,x2i各自趋于一致,x3i,x4i能收敛至0.

现对定理3进行证明,对于任意s∈R,如下不等式恒成立:

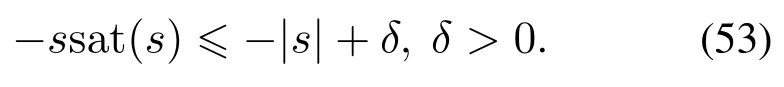
联立式(44)-(45)(53),化简可得

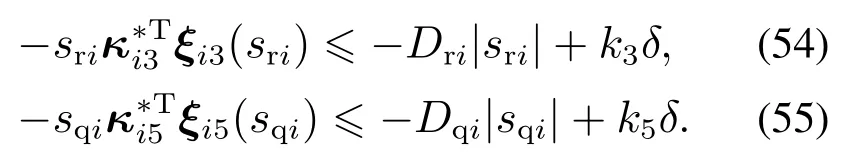
联立式(25)(32)(40)-(41)(54)-(55),得

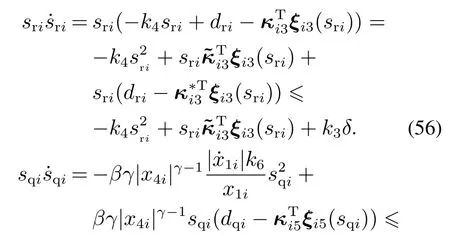
选取全系统Lyapunov函数

对式(58)求导,并结合引理4与式(56)-(57)可得

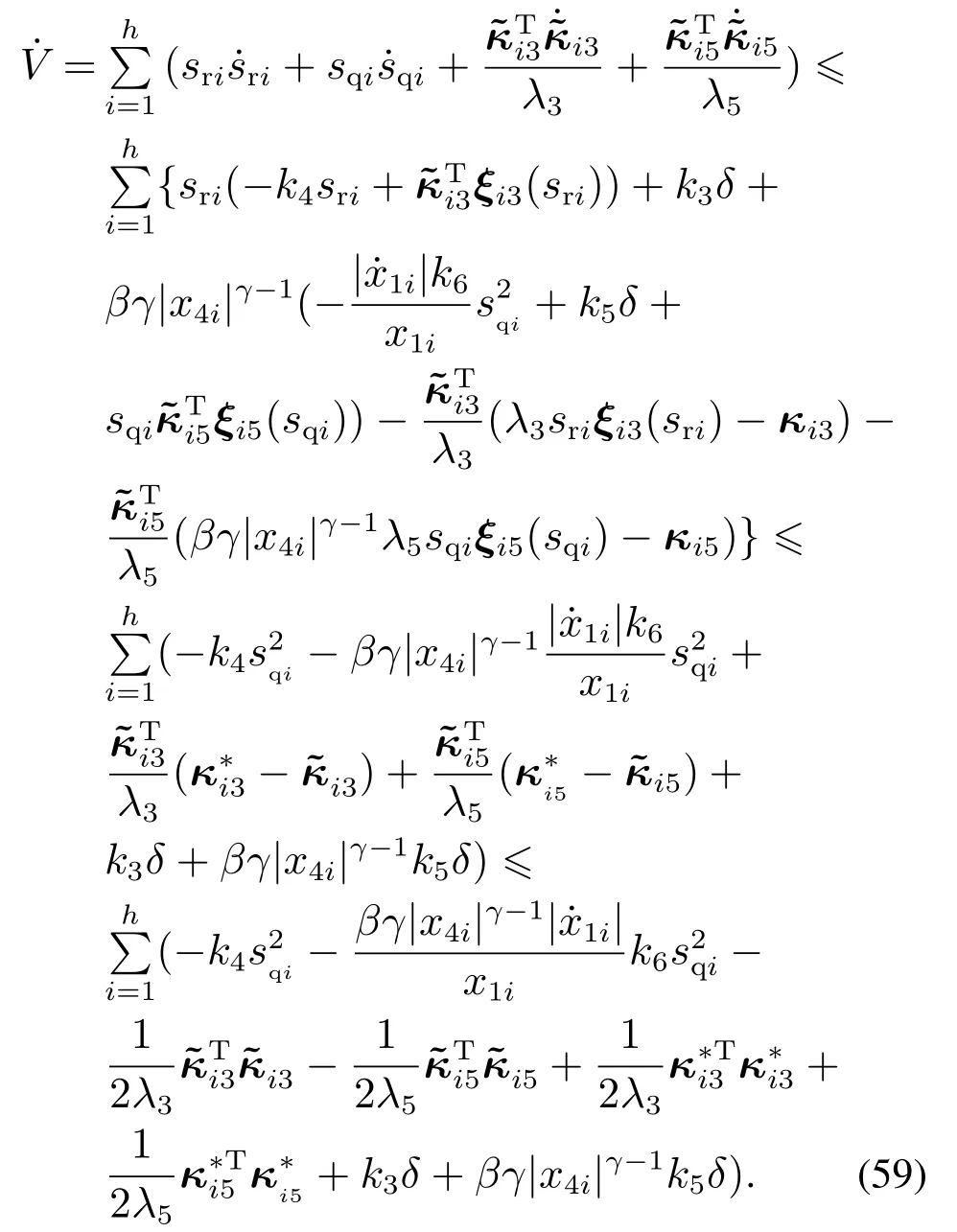
令φ=min{k4,βγ|x4i|γ−1},并取正常数

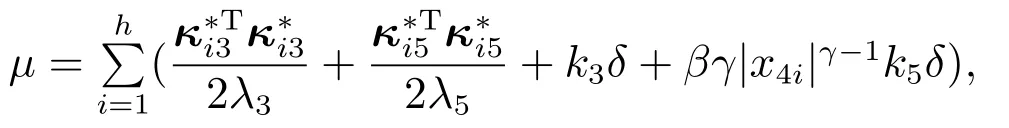
则式(59)可化为如下形式:

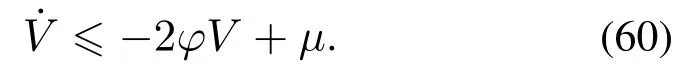
引理5对任意给定的一阶线性非齐次微分方程

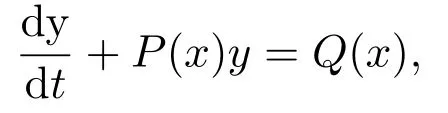
其通解形式如式(61)[24],C为任意常数.

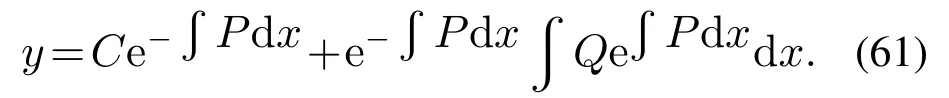
由引理5可得式(60)的解为

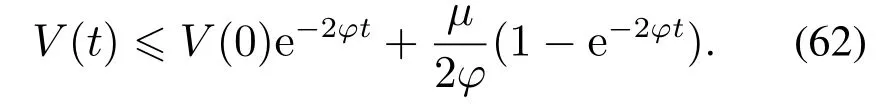
联立式(59),进一步可得

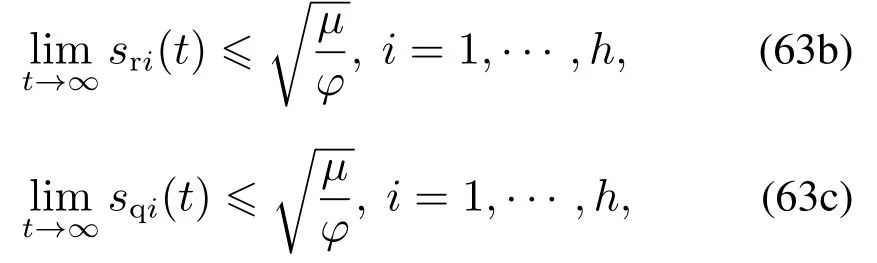
则V,sri,sqi最终一致有界,需要指出的是,虽然在上述证明过程中当t→∞时V,sri,sqi才能收敛至零点的充分小邻域内,但由于V 主要呈指数型衰减,在实际仿真实验中,可以通过增大衰减系数与降低系统初值的办法提高收敛速度,以保证V,sri,sqi能在有限时间内收敛,具体方法为选取k4,k6,β,γ为较大的合适值,使得指数衰减系数为φ=0.5,并选取λ3,λ5足够大,δ足够小,使得µ任意小,具体参数取值还需通过仿真实验确定.进一步结合定理1-2,可知定理3证毕.

为改善控制指令的终点发散现象,针对式(33)结合x1i设计两阶段滑模自适应趋近律

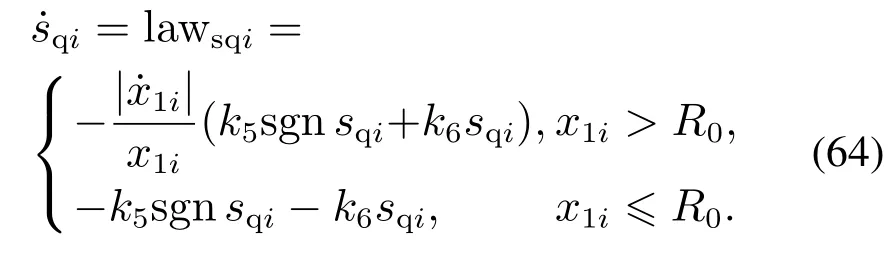
可得模糊参数自适应律与视线方向控制指令为

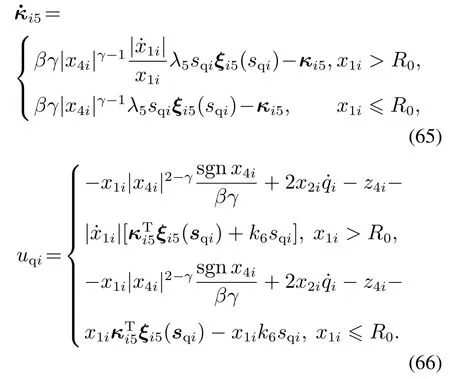
受篇幅所限,本文中仅对x1i>R0的情况进行证明,x1i≥R0时同理可证.

5 仿真实验

为验证协同制导律(50)(66)(简称律1)的有效性,现由3枚制导炮弹组网,在通信拓扑(如图3)、网络化弹药初始参数(见表1)、目标初始参数(见表2)、制导律参数(见表3)相同的情况下,现与含变结构项的制导律式(23)(34)(简称律2)对比,对机动形式不同的目标分别进行协同攻击仿真实验.

图3 网络化弹药通信拓扑Fig.3 Communication topology of network projectiles

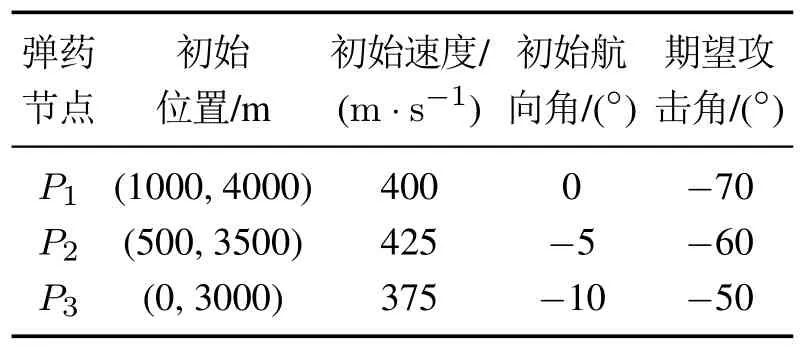
表1 网络化弹药初始参数Table 1 Initial parameters of network projectiles

表2 目标初始参数Table 2 Initial parameters of target

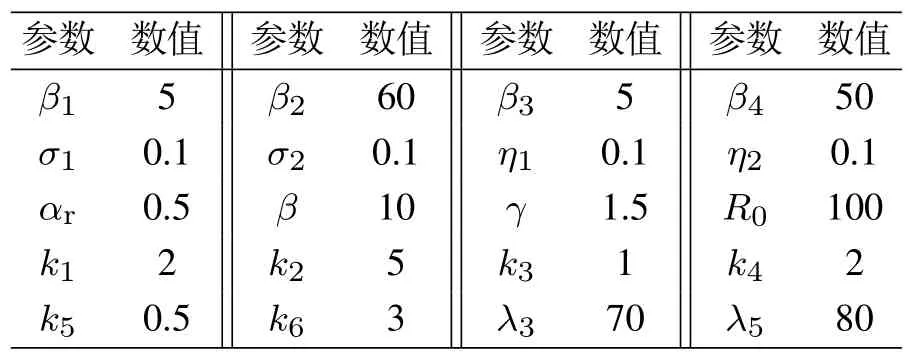
表3 制导律参数Table 3 Parameters of guidance law

为使定理3成立,经过多次仿真实验,确定控制参数

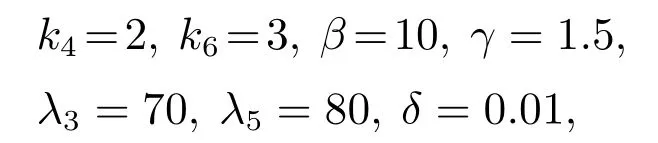
可以使指数衰减系数φ=0.5,且µ保持很小的值,同时令κi3,κi5初始值均为零,模糊隶属度函数采用下式,式中m=1,···,5.

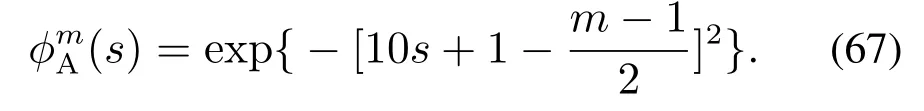
5.1 工况1:目标方波机动

此时,设定

仿真结果如表4与图4.

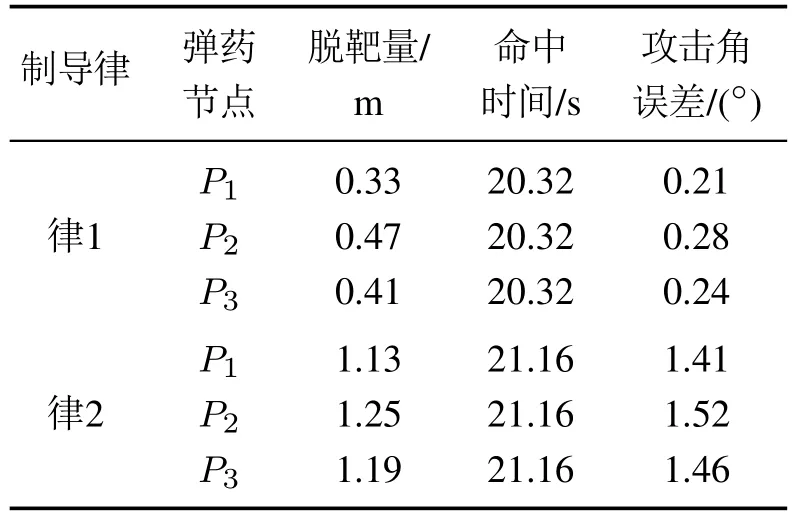
表4 工况1仿真结果Table 4 Simulated result under condition 1

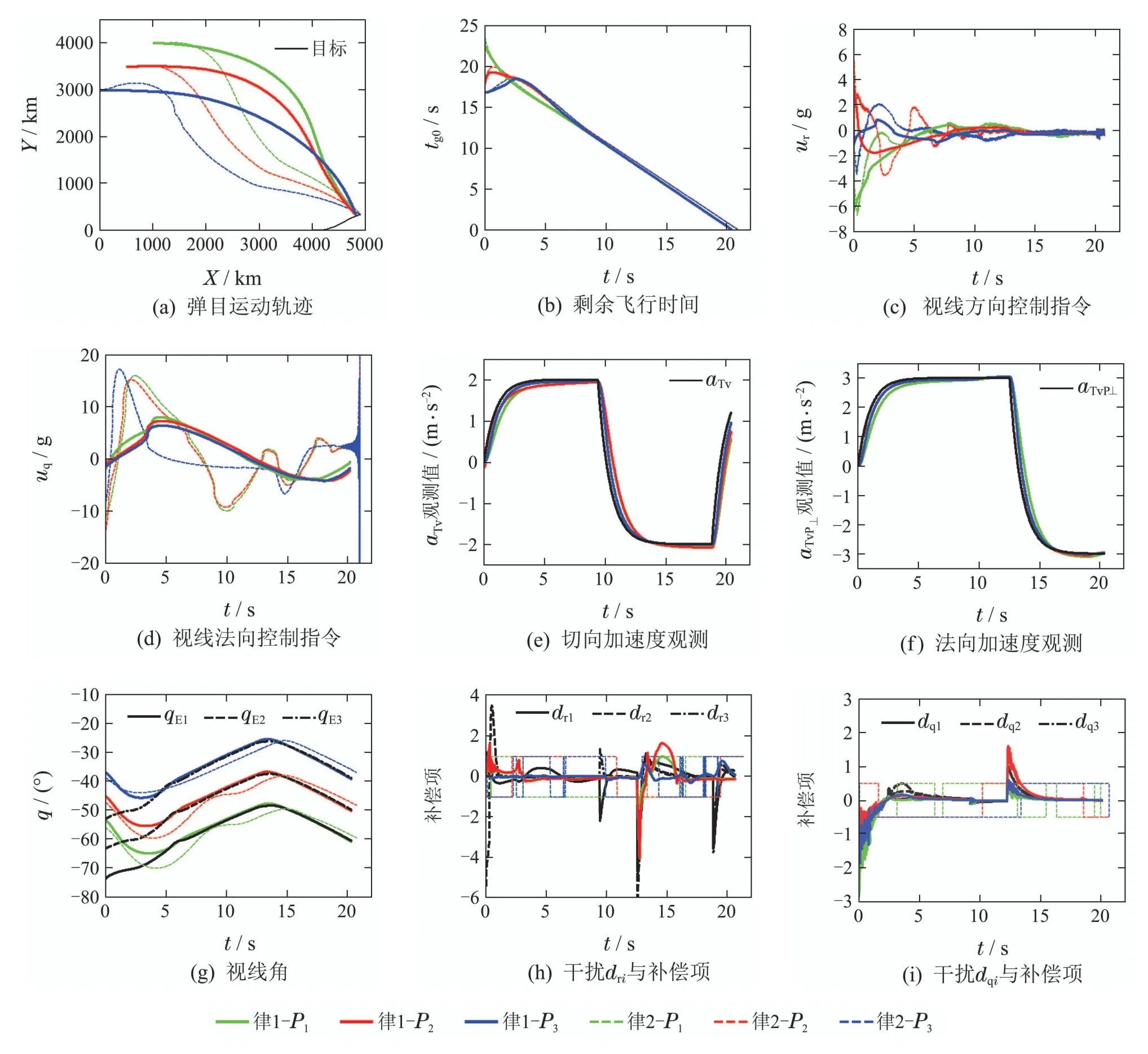
图4 工况1协同攻击仿真实验结果Fig.4 Simulated results of cooperative attack under condition 1

图4(a)为弹目运动轨迹,律1和律2均可用于网络化弹药协同攻击方波机动目标的末制导段,结合表4可知,律1优化了脱靶量与命中时间,且其弹道较为平直,有利于制导炮弹在制导过程中进行精细调节.由图4(b)可知,在律1和律2的作用下,网络化弹药的tgoi均能够自不同的初值在8 s左右逐渐趋于一致,并最终收敛至0,且律1收敛速度更优.图4(c)-4(d)分别为视线方向、法向的控制指令曲线,相较于律1和律2的uri,uqi的初始值、震荡幅度以及终点抖振幅度均较大,且随着弹目距离接近在终点处发散,外加其切换增益系数固定,易导致系统失稳,而律1通过模糊自适应逼近器的调节补偿,控制指令在整个制导过程中幅值较小、相对平滑,并在两阶段滑模自适应趋近律的作用下于终点处收敛,这满足了制导炮弹的控制性能要求.图4(e)-4(f)表明所设计的双ESO具有良好的观测性能,能够快速准确地观测出机动目标的切向、法向加速度真值,使制导律可以提供足够的可用过载补偿外界干扰,有效降低了制导炮弹的需用过载,同时有利于减小脱靶量与命中时间.图4(g)为视线角与期望视线角的变化情况,由于目标做方波机动导致期望视线角时变,律2视线角在跟踪过程中存在较大的超调震荡,这是由切换增益系数取值固定引起的,而律1通过模糊自适应调整参数取值,在6 s后能够稳定地保持视线角的收敛状态,表明视线角跟踪误差、视线角速率能在有限时间内收敛至零,验证了“第2.2节”中对系统状态有限收敛性分析的正确性.干扰项dri,dqi与对应的变结构项、模糊自适应逼近器补偿项如图4(h)-4(i)所示,目标机动给逼近补偿带来了较大困难,切换增益系数固定显然容易导致控制指令发散甚至系统失稳,模糊自适应逼近器其通过所设计的自适应律对模糊参数向量进行快速调整,较好地解决了变结构项带来的控制指令抖振问题,并从整体上逼近补偿了干扰,但其逼近能力有限,未能补偿局部跳变干扰.

5.2 工况2:目标正弦机动

此时,设定

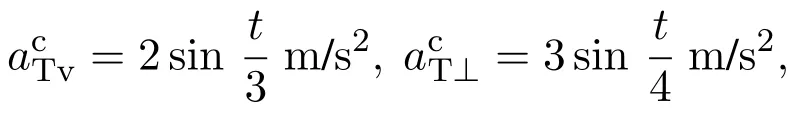
仿真结果如表5与图5.

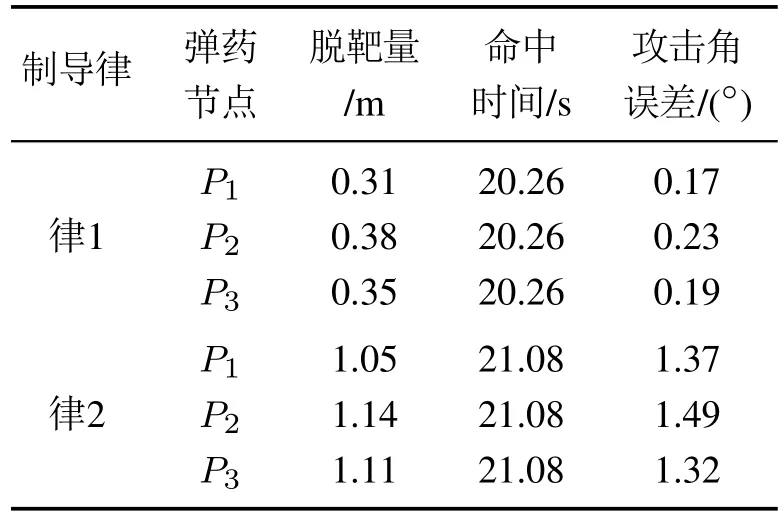
表5 工况2仿真结果Table 5 Simulated result under condition 2

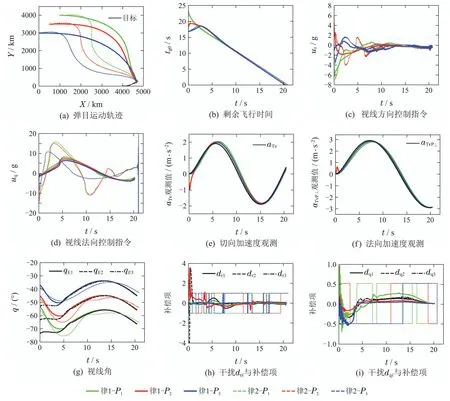
图5 工况2协同攻击仿真实验结果Fig.5 Simulated results of cooperative attack under Condition 2

图5(a)为弹目运动轨迹,律1和律2均可使网络化弹药协同命中正弦机动目标,结合表5可看出较律2,律1弹道更为平直,进一步改善了命中精度与命中时间.由图5(b)可知,在律1和律2的作用下,网络化弹药的tgoi均能够由不同的初值在7 s左右逐渐趋于一致,并最终收敛至0,验证了“第2.1节”中对系统状态有限收敛性分析的正确性,并且律1收敛速度更优.图5(c)-5(d)描述了网络化弹药视线方向、法向控制指令的变化情况,律2的uri,uqi在整个制导过程中较大,由于切换增益系数固定导致不同程度的震荡,而律1通过自适应调节模糊参数,法控制指令的变化较为平滑,并在终点附近有收敛趋势,这更加符合实际作战需求.图5(e)-5(f)表明所设计的双ESO观测性能良好,能快速准确地观测出目标加速度的真实值,为有效命中正弦机动目标提供了重要信息,使得网络化弹药可以提供足够的可用控制指令补偿外界干扰,有助于降低制导炮弹在制导过程中的对飞行控制性能的要求.视线角与期望视线角的变化情况如图5(g),由于切换增益系数取值固定,导致律2视线角难以稳定地收敛至期望视线角,而律1的模糊参数可自适应调整取值,保证在整个制导过程中视线角跟踪误差与视线角速率较快地跟踪正弦机动目标,在7 s后能够稳定地保持收敛状态,表明系统状态变量x3i,x4i能在有限时间内收敛至0.图5(h)-5(i)分别为干扰项dri,dqi与对应的变结构项、模糊自适应逼近器补偿项,由于律2含变结构项难以确定切换增益系数,在制导过程中难免产生抖振,难以实时补偿干扰,而律1的模糊自适应逼近器可以有效地削弱抖振,并较好地补偿了不确定干扰对制导性能的负面影响.

6 结论

针对大口径舰炮网络化制导弹药打击近岸机动目标的末制导段,设计了一种含攻击角约束的有限时间分布式模糊协同制导律,经模型建立、理论证明与仿真实验,现总结全文如下:1)双ESO模型精确快速地观测了机动目标切向、法向加速度;2)模糊自适应逼近器有效削弱了控制指令抖振,并对不确定干扰取得了较好的补偿效果,两阶段滑模自适应趋近律较好地改善了终点控制指令发散现象;3)严格证明了系统状态一致最终有界性与有限时间收敛性,在打击机动形式不同的目标时,均具备较好的协同制导性能,并且所需的其他外界信息均易通过现有成熟技术测得,具有一定的工程应用价值.