2019年广州市中考数学第25题的解题研究

广东省广州市真光中学

二次函数是初中数学的重要内容之一，也是初中数学与高中数学联系的纽带，高中阶段我们会继续深入地学习它.据学生反馈，关于二次函数及其图象的抽象度高，综合性强，因此学生普遍感到学习难度大，且其内容在中考中占有较大的比重.二次函数的试题能够较好地考查学生的函数与方程、数形结合、分类讨论和转化的思想方法，也能较全面地反馈学生的综合能力，因此，二次函数在中考中既是难点，也是热点.笔者研究了近几年广州市中考试题，现以2019年广州市中考数学第25题为例，把自己的一点想法撰写成文，与读者交流，请予以斧正.

1 试题呈现

已知抛物线G:y=mx2-2mx-3 有最低点.

(1)求二次函数y=mx2-2mx-3的最小值(用含m的式子表示)；

(2)将抛物线G向右平移m个单位得到抛物线G1.经过探究发现，随着m的变化，抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系，求这个函数关系式，并写出自变量x的取值范围；

(3)记(2)所求的函数为H，抛物线G与函数H的图象交于点P，结合图象，求点P的纵坐标的取值范围.

2 难点解读

本题主要考查二次函数的综合问题，解题的关键是掌握二次函数的图象和性质、图象的平移、二次函数的最值问题、函数与函数的交点问题，解题的难点在于学生能否利用数形结合等思想去解题.

对于第(1)问，

方法一把二次函数一般式配方成顶点式

由题意知m ＞0，因为y=mx2-2mx -3 =m(x2-2x+1)- m -3 =m(x -1)2- m -3.又因为(x -1)2≥0,m ＞0.所以m(x -1)2≥0.因此，m(x-1)2-m-3≥-m-3，即y ≥-m-3.当x=1时，y取最小值，最小值为-m-3.

方法二利用二次函数的顶点公式

因为抛物线y=mx2-2mx-3 有最低点，所以抛物线开口向上，顶点的纵坐标为函数的最小值.对称轴为直线把x=1 代入y=m×12-2m×1-3 =-m-3.

所以当x=1时，y取最小值，最小值为-m-3.

日常教学中需引导学生会求解含参数的二次函数的最值问题，其方法是把一般式配方成顶点式或者公式法去求解最值问题.学生对于遇到含有变量的问题，就会出现计算上的错误或者无从下手，因此我们要加强对含变量的类型的题目加强理解和训练.

对于第(2)问，

由题意得G1:y=m(x - m -1)2- m -3(m ＞0).所以抛物线G1的顶点坐标为(m+1,-m -3).

故y=-x-2(x ＞1).

第(2)问是考查函数图象左右平移以及将函数的参数方程化为普通方程.我们可以在人教版教材找到关于二次函数的图象左右平移的影子，但是没有系统阐述.平时教学过程中，我们老师应该重视教材，深挖教材，尤其是在初中教材当中没有深入研究的知识，但是在高中教材有的知识点.例如八下教材一次函数章节中，教材研究了一次函数图象的上下平移，那么很多学生自然就会想到左右平移又有什么规律呢? 此时，我们让学生画以下三组函数图象：(1)y=x与y=x+1,(2)y=2x与y=2x+1,(3)y=-2x与y=-2x-1，思考这三组函数图象是否可以通过左右平移来相互得到? 我们用最简单的一次函数来探究图象上下平移和左右平移，并总结图象平移的规律，那么我们在教二次函数图象平移时，就可以类比一次函数的图象平移的方法.深入探究教材，由简单到复杂，即有利于我们加深对一次函数和二次函数的学习，也有助于今后我们对三角函数等函数学习和理解.

对于第(3)问，

方法一通过画出两个函数图象，找到交点的临界位置

我们画出这两个函数图象，由图1可知，-4＜yp ＜-3.

方法二通过联立方程组求得交点坐标

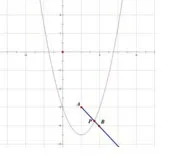
图1

因为xp ＞1，所以，因为，4m2+1＜(2m+1)2,m_＞0，所以，即，-1＜即，所以，-4＜yp ＜-3.虽然我们可以用代数方法去求解第(3)问，但是它对学生的计算能力和逻辑推理能力的要求比较高，对于大多数中学生来讲，还是很难掌握.因此数形结合思想在解决比较复杂的代数问题就会显得比较简捷.

2019年广州市中考数学第25题虽说综合性强，所涉及的基本知识并不复杂，因此只要学生基础扎实，勤于总结，善于灵活运用，便可顺利解答.当然我们掌握的知识和方法越多，产生的解法会越多，解法会越简捷，也能在现有的认知水平上提升一个档次.

3 研题心得

每道题目在剖析后都会显得简单，它的难处在于我们平时缺乏思考，缺乏大胆尝试，缺乏深入探究教材.例如我们在讲述一元二次方程ax2+bx+c=0 有根时，我们会探究两根之和以及两根√之积，此时学生自然会思考两根之差? 不妨设(其中Δ =b2-4ac，代入得到也可以通过韦达定理得到：两根之差的绝对值就是抛物线与x的两个交点之间的距离，熟悉了这个探究过程，我们就很容易求解2016年广州市中考数学第24题中的第三问(其中AB=|x1-x2|).因此，我们要重视教材的使用，教学中重视知识的形成的过程，精心选择教学素材，合理组织教学，把课堂活动时间、思考的时间还给学生，把观察、归纳、概括、探究、交流的机会还给学生，把问题的提出过程、知识的获取过程、结论的探究过程、认识的升华过程、思路的分析过程还给学生.同时，也要强化理解，多一点让学生用自己的语言来表述学习内容的内涵，在具体情节中辨析其中蕴含的数学知识，灵活运用数学基本知识、技能、思想方法分析问题和解决问题.