深入解读高中教材中的线性相关系数

广东省中山市实验中学

高中教材中对相关系数的介绍比较少，学生和老师对它的理解也不够深入，只是知道它怎么用，但是不知道它为什么可以这样用.可谓知其然但不知其所以然.所以本文借助教材和其它相关资料，对相关系数的有关知识做个深入的解读，使大家更全面和彻底的理解它，从而更好的加以应用.

1 什么是相关系数

在人教A版《普通高中课程标准实验教科书数学必修》中对相关系数在第92页“阅读与思考”部分的第一段中有这样的描述：“我们知道，两个变量x和y正(负)相关时，它们就有相同(反)的变化趋势，即当x由小变大时，相应的y有由小(大)变大(小)的趋势，因此可以用回归直线来描述这种关系.与此相关的一个问题是：如何描述x和y之间的这种线性关系的强弱?”.显而易见，教材中这句话表明了相关系数引入的必要性，同时也说明了引入相关系数的主要作用就是判断两个变量线性关系的强弱.

接着在第二段中写到：“统计中用相关系数r来衡量两个变量之间线性关系的强弱.若相应于变量x的取值xi，变量y的观测值为yi(1≤i ≤n)，则两个变量的相关系数的计算公式为：

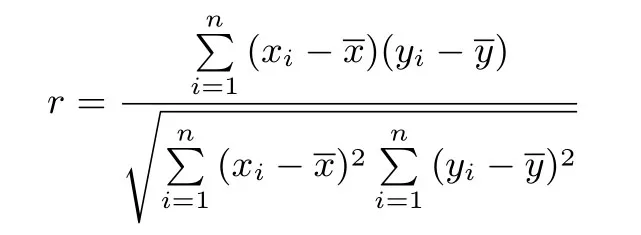
从而顺理成章的给出了相关系数的计算公式.但是个人觉得，这个公式的出现有点突然，很多师生对它的理解仅仅停留在会用的阶段，至于它怎么来的?分子分母的意义是什么?却知之甚少.

2 从几何直观上理解两个变量正(负)相关以及其相关性的强(弱)

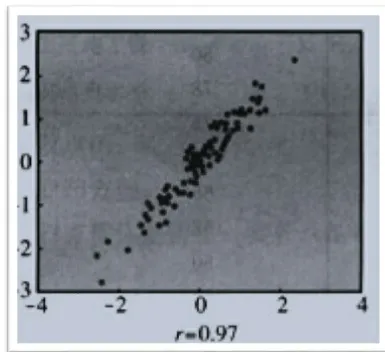
图1

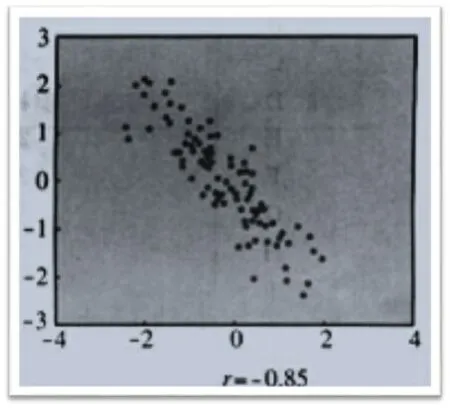
图2

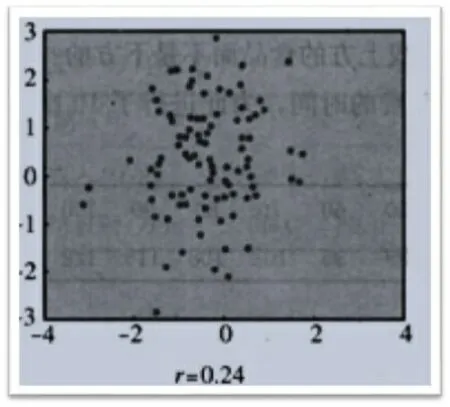
图3

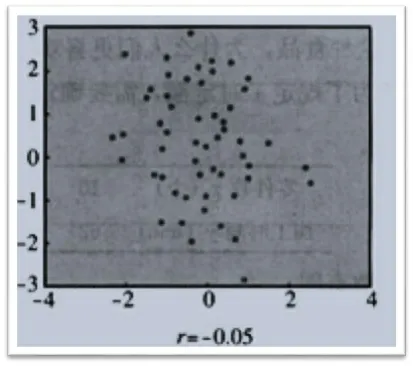
图4

(1)图1，图2中样本点都是带状分布，而且数据好像集中在某一条线附近，反映了变量x和y之间很强的线性相关关系.而图3，图4中样本点分布无明显规律，杂乱无章，所以两个变量的线性相关关系很弱.

(2)图1中这些点散布在从左下角到右上角的区域，所以是正相关.图2中这些点散布在从左上角到右下角的区域，所以是负相关.

另外上面的每个图中都对应了相关系数r的一个值，或大或小，或正或负.这个值怎么解读呢?教材中介绍说：“当r为正时，表明变量x和y正相关；当r为负时，表明变量x和y负相关”.另外教材还写到：“统计学认为，对于变量x,y，如果r ∈[-1,-0.75]，那么负相关很强；如果r ∈[0.75,1]，那么正相关很强”.

这里我们很容易产生个疑问，为什么|r| →1时相关性越强呢?但是教材中却没有介绍.

3 如何理性的理解正相关，负相关与的符号的关系

下面我们从公式本身出发尝试解释正负相关和的符号之间的关系.

(1)正相关：事实上，从样本的总体角度来看，对于每一个数对(xi,yi)，如果中求和项大部分是正数的话，也可以理解为xi和yi同时同方向偏离各自的平均值，即使有少数样本点不同向偏离，如果样本点足够多也不会影响即r ＞0.所以我们说变量x,y为正相关.

(2)负相关：从变化趋势上来看，对于每一个数对(xi,yi)，如果中求和项大部分是负数的话，也可以理解为当xi大于其均值时，yi却小于其均值.也就是二者反方向偏离各自的平均值，即使有少数同向偏离，如果样本点足够多也不会影响解为xi和yi同时同方向偏离各自的平均值，即使有少数样本点不同向偏离，如果样本点足够多也不会影响即r ＜0.所以我们说变量x,y为负相关.

(3)不相关：如果样本中同方向偏离的和反方向偏离的样本点的个数相当时，此时解为xi和yi同时同方向偏离各自的平均值，即使有少数样本点不同向偏离，如果样本点足够多也不会影响的值接近于零.我们认为二者不相关或者相关关系很弱.

4 如何理性理解相关关系的强弱和的大小关系

笔者查阅了相关资料有两种解释方式比较容易使高中师生接受.

(1)从柯西不等式的角度解读

从r的计算公式可以看出，分子和分母刚好与柯西不等式的两端相似.即其中ai,bi ∈R，并且当且仅当bi=0或存在一个数k，使得ai=kbi时等号成立.

(2)从最小二乘法的角度解读

在教材《普通高中课程标准实验教科书数学选修2-3》第80页中，为了让所有样本点离直线的“整体距离”的值最小，构造了函数

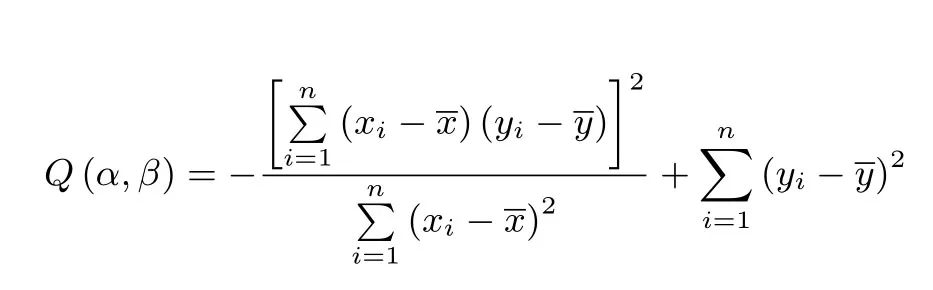
从而可知：

5 相关系数r和相关指数R2的关系

(1)相关指数R2的介绍

《普通高中课程标准实验教科书数学选修2-3》中介绍说：

(2)相关系数r和相关指数R2区别和联系.