互换利差的横向与纵向交易策略

程昊　李鹤然

摘   要：在理论分析的基础上，分别构建互换利差的横向交易策略和纵向交易策略，实证检验结果显示：对于横向交易策略，无论构建多因子模型还是统计套利策略均不能盈利。因此，投资者基于市场基本面对互换利差的供需关系和未来走势进行主观判断最适用于互换利差的横向交易策略。对于纵向交易策略，通过分析互换利差的利率期限结构发现，构建骑乘策略可以获得较为稳定的超额回报。

关  键  词：互换利差;横向交易策略;纵向交易策略;统计套利;骑乘策略

中图分类号：F830.593     文献标识码：A      文章编号：2096-2517（2020）01-0019-13

DOI：10.16620/j.cnki.jrjy.2020.01.003

一、引言及文献回顾

随着我国利率互换市场的发展，利率互换逐渐成为债券市场重要的交易品种。对于相同期限的国债和利率互换，二者信用资质相仿、现金流实现方式相似、流动性相差无几。因此，互换固定利率与国债利率之间可能存在稳定的相关关系，而互换利差（互换交易中固定利率报价与同期限国债利率的差额）交易策略，也逐渐成为债券市场中重要的交易策略。

国内外学者对互换利差的影响因素进行了深入的研究。国外方面，He（2000）从融资成本差异、流动性风险溢价和持有长期利率互换的风险溢价角度，对互换利差的期限结构进行了探讨[1]。Lekkos等（2001）通过建立VAR模型，从实证角度验证了流动性、利率水平、期限结构斜率、利率波动性和违约风险因素对美国利率互换利差的影响[2]。Hui等（2008）发现在不同时期，流动性风险和信用风险对于互换利差的影响程度存在差异[3]。国内方面，杨辉等（2008）通过回归分析，探讨了融资成本、流动性风险溢价、违约风险、利率期限结构和股票市场波动性对5年期互换利差的影响[4]。程昊等（2018）构建无套利定价分析框架，分别分析了无套利定价成立和失效时互换利差的影响因素[5]。

本文首先对无套利定价理论进行回顾，探讨互换利差的构成因素，然后从横向角度，分别构建多因子模型和统计套利策略，检验对于某一期限互换利差的交易策略效果;从纵向角度，利用互换利差期限结构形态，检验综合多个期限构建交易策略的效果。

二、理论分析

对于期限相同的国债和互换交易，当两者信用资质相仿、现金流实现方式相似、流动性都比较好时，可以通过无套利定价方式得到二者利率之间的关系。若投资者想获得固定利率，有两种选择：一是在回购市场中融资并购入国债;二是进入相同期限的互换，收取固定端利率，支付浮动端利率。因此，在无套利定价的思想下，互换利差的理论价值应等于合约期内一系列互换浮动端利率现值之和减去一系列国债回购利率现值之和。然而，无套利定价需要满足两个条件，即不存在隐形交易成本和市场供需关系保持稳定。

在真实的市场中，由于交易约束和残留风险等隐性成本的存在，投资者可能很难在互换市场和国债市场之间进行无成本套利。交易约束包括投资者参与互换交易的限制、考核期與利差收敛区间的错位等。残留风险包括现金流错配、借券逼空等套利退出风险。由于交易约束和残留风险在真实市场中无法被彻底解决和完美规避，投资者不能有效参与互换利差套利，或者参与套利交易获得的收益与预期不符，因此无套利定价失效。

即使交易约束和残留风险等阻碍套利机制发挥作用的市场摩擦不存在，互换市场和国债市场中的供需失衡依然可能使互换利差偏离其公允价值。如（1）式所示，互换利差（rswap-rtreasury）可以拆分为：一是利率互换固定端利率与其未来一系列浮动端利率现值之和的差异（rswap-rfloat）;二是未来一系列利率互换浮动端利率现值之和与国债回购市场中回购利率现值之和之间的差异（rfloat-rrepo）;三是未来一系列国债回购利率的现值之和与国债收益率之间的差异（rrepo-rtreasury）。当市场供需平衡时，（1）式中的第一项和第三项均为0，互换利差完全由未来一系列互换浮动端利率现值之和与国债回购利率现值之和差异决定（后文中简称互换浮动利率与国债回购利率之差）。

rswap-rtreasury=（rswap-rfloat）+（rfloat-rrepo）+（rrepo-rtreasury）（1）

当市场供需关系稳定时，互换浮动利率与国债回购利率之差可能受到信用风险和流动性等多方面因素的影响。就信用风险而言，由于互换浮动端参考利率FR007由信用债和利率债的回购利率两方面共同决定，而国债回购利率仅由利率债回购利率决定，因此当市场信用风险上升时，利率债由于其高安全性，相对于信用债更容易融入资金，国债回购利率与FR007之间的利差被拉大， 互换利差上升。就流动性因素而言，一方面，在利率互换诞生初期，其流动性较国债稍差，因而互换利差中包含一部分流动性溢价，然而近年来互换市场逐步发展完善，活跃程度日益上升，流动性溢价对于互换利差的影响逐渐减弱;另一方面，由于国债回购需要不断滚动融资，而利率互换协议一旦签订即可锁定未来一段时间的交易期，在不考虑信用风险的情况下，国债回购相对于利率互换存在一定的操作风险溢价，回购市场流动性越紧张，操作成本越高，则互换利差越小。

由（1）式可知，互换市场与国债市场的供需关系也会对互换利差产生影响。利率互换市场与利率期限结构有关。 从期限结构的水平因素角度看，当利率水平上升时， 投资者为了对冲利率上升风险，选择支付固定利率，互换多头方需求上升，互换利率上升，互换利差扩大。此外，在国外市场，抵押支持债券（MBS）的投资者可能面临提前偿付风险：当市场利率下降时， 借款者可能会执行提前偿付权，投资者的组合久期下降。 为了对冲提前偿付风险，投资者希望收取固定利率， 收取固定端需求上升，互换利率降低，互换利差下降[6]。从期限结构的斜率因素角度看，一方面，当收益率曲线陡峭时，预期浮动端在未来需要支付的利率增加， 其违约概率增大，固定端会要求支付更低的利率作为对手方违约风险的补偿[7];另一方面，收益率曲线斜率下降时往往预示着宏观经济条件恶化，为了规避利率变动的不确定性，部分企业更愿意支付固定利率，互换利率上升，互换利差扩大[2]。国债回购市场的供需关系主要考虑债券市场与股票市场的替代关系，当股票市场表现较差时， 投资者会更偏好债券市场，而国债相对于互换更具有风险规避作用，其需求量会增加，价格上升而收益率下降，从而互换利差扩大。因此，股票市场预期收益率可能与互换利差存在负相关关系。

三、横向交易策略

由上述的理论分析可知，互换利差的影响因素比较复杂。具体而言，隐形约束和残留风险可能使无套利定价失效;当无套利定价成立时，互换利率会受到互换浮动利率与国债回购利率之差、信用风险、流动性因素、利率期限结构和股票市场替代效应等多方面因素的影响。基于此，本文首先从横向角度，分别构建多因子模型和统计套利策略，检验某一期限互换利差的交易策略效果。

（一）多元回归分析

由理论分析可知， 互换利差的影响因素众多，且大多不可量化， 本文选取一些具有代表性的变量，分析其对互换利差影响的情况，分别为互换浮动利率与国债回购利率之差、市场信用风险、利率水平、利率波动率、利率期限结构的斜率和股票市场预期收益率。本文分别选择1年和5年以衡量短期和长期互换利差的影响因素。

1.变量选取

以互换利差差分序列构建回归模型，具体的变量选取如下：

（1）互换利差（spread）：以市场中最活跃的互换品种——参考FR007的互换固定利率与国开债收益率之差作为互换利差。选取国开债而非国债不仅是为了规避税收因素，更是出于实用角度，因为投资者大多通过交易国开债实现与互换之间的套利。

（2）互换浮动利率与国开债回购利率之差（cost）：在无套利定价成立且供需平衡时，互换利差应由两个浮动利率之差决定[5][8]。Repo互换浮动端利率以FR007表示， 由于利率债融资的便利性， 金融机构一般采取隔夜滚动融资，回购成本约为R001+xbp。由于xbp在计算差值时被抵消，本文以FR007-R001作为回购利率之差的代理变量。

（3）市场信用风险（default）：利率互换和国开债由于其发行/交易主体的差异，当市场信用风险上升时，互换利差扩大[1][9]。由于国内利率互换市场的交易主体大多为银行、证券等金融机构， 本文使用AAA商业银行普通债收益率与国开债收益率的利差作为信用风险的衡量指标。

（4）利率水平（level）：为了与投资者的交易习惯相符， 本文选择10年国债收益率来衡量市场利率水平。

（5）利率期限结构斜率（slope）：利率期限结构的斜率对于互换利差的影响通过市场信用风险和互换交易供需关系两方面来体现[10]。本文使用5年期国债收益率与1年期国债收益率之差作为利率期限结构斜率的代理变量。

（6）利率波动性（vol）：利率波动性通过影响市场信用风险影响互换利差[11]。本文以10年期国债收益率的30天滚动标准差作为利率波动性的衡量指标。

（7）股票指数（stock）：考虑到股票投资与债券投资可能存在的替代效应[9]，本文选择沪深300的日收盘价作为股票市场表现的衡量指标。

除上述因素外，影响互换利差的因素还包括隐性成本、市场流动性、市场供需关系等很多难以量化的因素，为了保证研究结论的可靠性，本文没有尝试为这些指标选取代理变量。

2.回归结果

本文首先对各变量进行差分处理，以各解释变量的滞后项预测未来互换利差的变动。此外，考虑到自身变动对互换利差的影响，本文将互换利差变动的滞后项作为被解释变量代入模型。由于债券市场估值收益率公布时间较晚，投资者不能以当日估值收益率进行交易，投资者以上一日收益率预测的当日收益率无法实现，因此本文选择以滞后二阶的被解释变量预测互换利差的变动。 样本区间选择2012年11月1日至2018年7月31日。

（1）短期互换利差

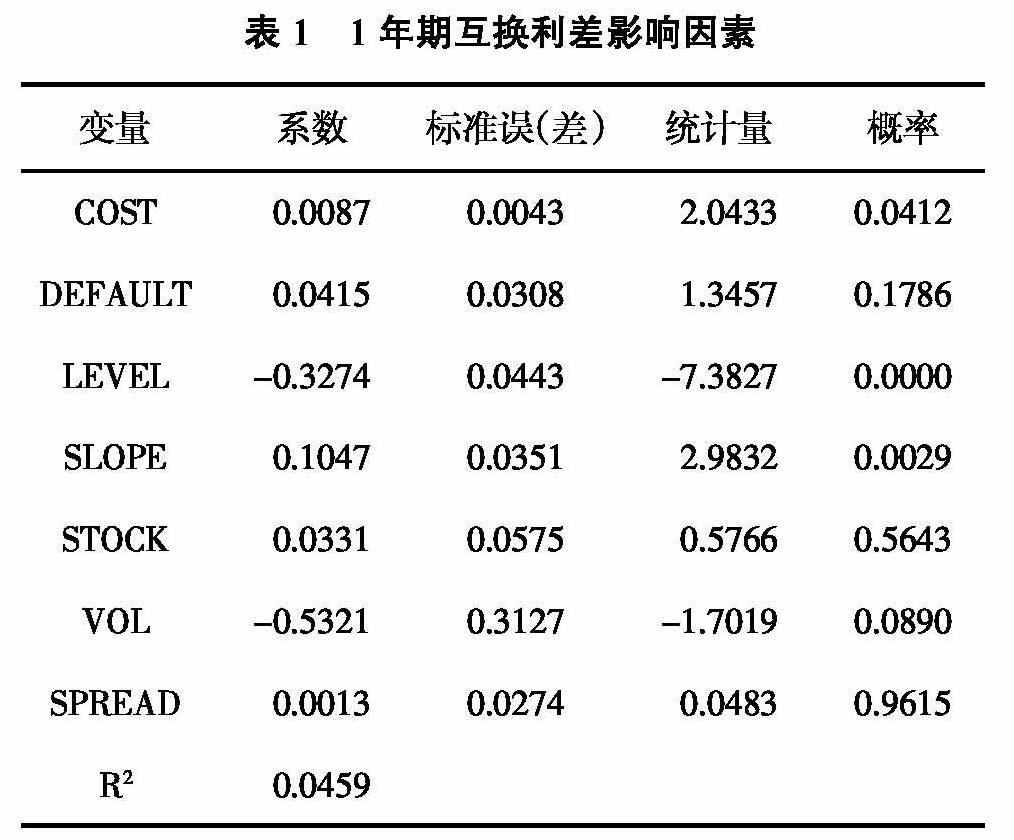
表1给出了各变量对1年期互换利差变动的影响情况。由表1可知，对于互换利差有显著预测效果的变量是利率水平值和利率期限结构的斜率。

实证结果与理论分析结论存在较大差异。a.互换浮动利率与国开债回购利率之差。在理想情况下，未来一系列互换浮动利率与国开债回购利率之差的现值之和是互换利差的内在价值，因此两个变量应正相关。实证结果显示，这一结论成立，然而其显著性程度并不高。一方面，由于国开债回购利率数据无法获得，本文以R001+xbp作为国开债回购利率的代理变量，存在一定偏误。另一方面，此处的收益率之差应为互换存续期内未来每笔现金流的现值，然而受限于數据可得性，本文只能以两个浮动利率之差的滞后项作为代理变量，因而产生较大偏差。b.信用风险。理论分析认为，信用风险与互换利差正相关。然而，就我国互换市场而言，市场参与者多为国有企业， 主体违约概率本身处于较低水平，且互换市场发展逐步完善，投资者的违约损失率大大降低，因此市场信用风险的影响不显著。c.利率水平。理论分析认为投资者可能为了对冲利率上升风险而支付固定利率，互换利差与利率水平正相关。然而实证结果显示二者之间存在显著的负相关关系，图1也证明了这一结论。这种现象可能源于互换与国开债市场交易性质和定价机制的差异。就交易特性而言， 互换与国开债参与者的需求不同，国开债参与者较为单一，投资目的相对一致;而互换参与者较为多元化，以套期保值、投机等多种目的参与市场，其趋势性较国开债稍弱。就定价机制而言，互换的参考利率为FR007，采用每日9：00至11：00盘中银行间质押式回购利率取中位数得到，由于回购市场上午成交的多为银行，且银行R007交易量在全天占比也近一半， 因此FR007大多会落在银行回购利率上限内。 银行回购利率受SLF利率走廊上限等因素限制，相比于非银行机构交易利率的市场化程度低，波动性较小。因此，互换利率的趋势性也相对较弱。在这两个因素的共同作用下，当利率上升时，国开债上升的幅度高于互换利率上升的幅度，互换利差下降，互换利率与利率水平呈现负相关关系。d.利率期限结构的斜率。利率期限结构的斜率与互换利差正相关，与理论分析结论相反。可能源于互换期限与利率期限结构的期限不匹配。理论分析中互换利差与利率期限结构斜率负相关描述的是长期利率期限与互换期限相一致的情况，本文短期互换利差的期限为1年，而利率期限结构的斜率以5年与1年国债收益率之差表示。可能的原因为，5年和1年期的互换具有替代效应，当期限结构的斜率上升时，即5年期相对于1年期的利率较高，则投资者偏好收取5年期的固定利率， 支付1年期的固定利率，1年期互换的需求增加，互换利率上升，互换利差扩大。因此，互换期限之外的利率期限结构斜率与互换利差正相关①。e.股票预期收益率。金融市场中，股票与债券之间并不是简单的替代关系，互换利差与股票收益率之间的关系并不显著。f.利率波动。由于信用风险对于互换利差的影响并不明显，而利率波动主要通过影响信用风险影响互换利差，因此，利率波动对于互换利差的影响亦不显著。

3.对比分析

上文分别给出了对价差序列运用简单的反转策略和动量策略的结果。由此可知，反转策略比动量策略更适合运用于价差序列，然而一旦考虑交易成本，两种策略均失效。

针对动量策略，由于本文检验的是互换利率与国开债收益率的价差序列，即使互换利率或国开债收益率本身的价格序列由于投资者的非理性认知或投资者的追涨杀跌行为而产生一定的趋势，但是二者价格相减后，其趋势性被大大抵消，动量策略缺乏内在的逻辑，因此动量策略失效。

针对反转策略，互换利差存在内在的均值回复特性。相同期限的互换利率与国开债收益率具有相似的信用资质， 且二者的现金流实现方式相仿，因此，互换利率与国开债收益率应具有相似的定价机制，二者的利差存在内在的回归机制（互换利差的公允价值应为未来一系列互换浮动利率与国开债回购利率之差的现值之和）， 一旦其大幅偏离公允价值， 套利者即会进行反向操作使其回复公允价值， 因此互换利差应围绕其公允价值上下波动，在不考虑交易成本时反转策略有效。然而，一方面，互换利差的公允价值难以定价（未来一系列利差的现值之和难以准确量化）;另一方面，与期限利差在期货合约到期时一定会归零不同，互换利差尽管存在内在的回归逻辑， 却缺乏到期交割的硬性回归要求，而且投资者在互换与国开债之间套利存在如交易约束和残留风险等市场摩擦，套利交易可能无法完成，互换利差是否会回归公允价值以及何时回归均存在一定的不确定性。因此，互换利差的反转效应较弱，在现实的金融市场中，反转效应的盈利不足以抵消交易成本，反转策略不可用。

此外，利率互换作为市场中重要的套期保值工具，其价格较易受到市场中供需关系的影响。若互换市场的供需关系发生变化而国开债市场的供需關系保持不变，互换利率变动而国开债收益率保持稳定，则统计套利的理论基础“一价定律”失效，因此统计套利无法捕捉供需关系变动对互换利差的影响。相似地，国开债供需关系变化会对互换利差带来相反的影响。

四、纵向交易策略

上文主要探讨了横向交易策略，即针对某种期限互换利差的交易策略，接下来，结合互换利差的期限结构特点，从纵向角度构建交易策略。

纵向角度的策略涉及到互换利差的期限结构问题。 图5给出了1年、2年和5年的互换利差曲线。由图5可知，大多数时候，1年期的互换利差高于其他期限，而其他期限之间的互换利差没有显著差异。图6进一步给出了2年期互换利差与1年期互换利差之差，该差值基本在0以下波动，说明2年与1年互换利差的期限结构是向下倾斜的。

在大多数情况下，1年期的互换利差高于2年期的互换利差，这主要是国开债的期限结构斜率要高于互换利率的期限结构斜率导致。如图7所示，2年期与1年期国开债的利差在大多数情况下高于互换的利差，且其波动更为剧烈。这可能源于国开债与互换定价机制的差异。互换浮动端参考利率为FR007， 与国开债收益率相比，FR007由于参与者结构、定价机制以及央行利率走廊的控制等原因波动较小，投资者不愿意为其支付较高的溢价，因此，远期市场互换利率（Repo）互换的期限结构相比国开债的期限结构更加平坦。

投资者可以针对这一现象，利用2年期与1年期的互换利差，构建持有期为1年的骑乘策略赚取超额收益（持有期为1年与一般公司考核期相对应）。参考袁志辉（2018）[12]，骑乘策略的数学推导如下：

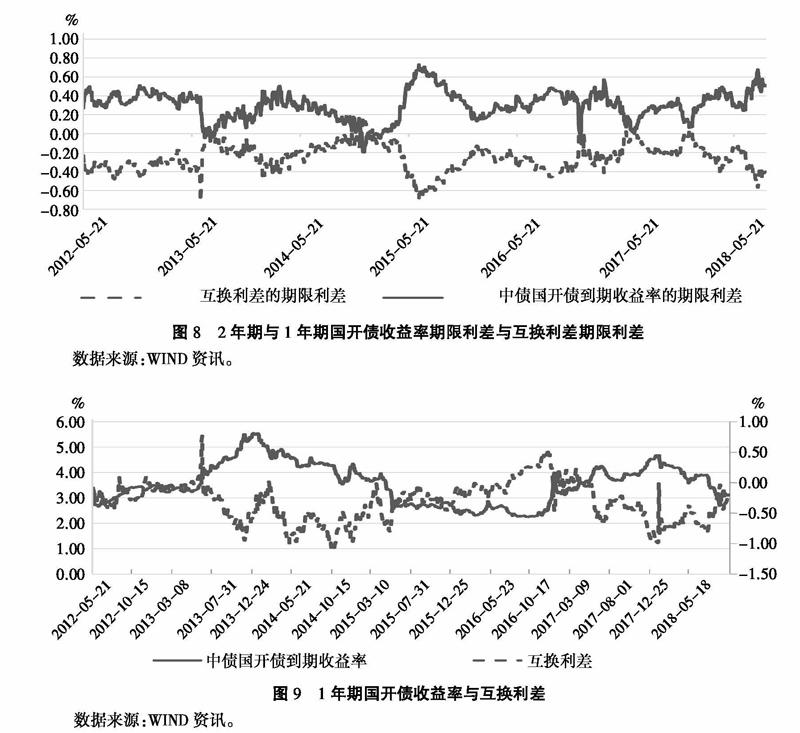
由图8和图9可知，2年期和1年期互换利差的期限利差走势与国开债收益率的期限利差走势基本一致，然而由于互换利差是两个收益率之差，趋势性被消除，利率风险在一定程度上被规避，因此其波动比国开债的波动小很多。这表明在具有相似斜率的情况下，互换利差上行的概率比国开债收益率上行的概率小，因此本文预计利用互换利差构建的骑乘策略比国开债构建的骑乘策略更为稳定。

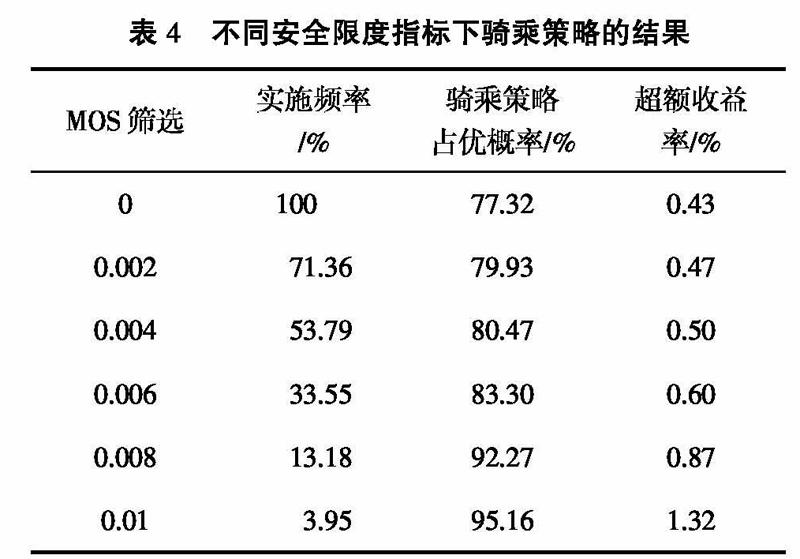
本文分别设置0、0.002、0.004、0.006、0.008和0.01为安全筛选指标，表4给出了根据不同安全筛选指标构建骑乘策略的结果。 由表4可知，即使不设置安全筛选指标， 骑乘策略的胜率也高达77.32%， 说明利用互换利差构建骑乘策略可以获得较好且较为稳定的回报，且MOS取值越大，骑乘策略的实施频率越低，策略胜率越大，骑乘策略的超额收益率越高， 说明MOS确实可以起到“安全垫”的作用。

基于此，本文构建了更贴合实际的投资策略，如图10所示。在t=0时刻，投资者需判断是否开仓：一方面，当安全限度指标满足一定条件时，投资者可以选择利用骑乘策略赚取超额收益; 另一方面，当互换利差大幅偏离其公允价值，偏离程度足以弥补套利交易的交易成本时，投资者也可以通过套利策略赚取超额收益（此处仅考虑国开债收益率大幅高于互换利率的情形，相反情形暂不纳入策略构建范围）。若满足上述两个条件之一，投资者可以买入2年期国开债，卖出2年期互换（支付固定利率，收取浮动利率），进行开仓操作。一旦开仓，投资者要在t=1时刻判断骑乘策略收益率是否高于套利策略收益率，若骑乘策略收益较高，则在t=1时刻平仓获得骑乘超额收益; 若套利策略收益较高，则选择持有到期，在t=2时刻获得套利交易超额收益。在实际操作中，投资者需检验利差序列的特性，根据序列特征更严谨地设置相应开平仓条件。

五、结论

基于无套利定价理论，对互换利差的影响因素进行了深入剖析，并对横向交易策略和纵向交易策略进行实证研究，结论如下：

第一，在横向策略方面，本文分别利用多因子模型和统计套利方法对互换利差的交易策略进行实证分析。多因子模型的结果显示：对于短期市场，利率水平因素、市场流动性和利率期限斜率因素对互换利差有显著影响;对于长期市场，仅有利率水平因素会显著影响长期互换利差。此外，受限于数据可得性， 一些因素的指标选取存在一定偏误，因此，基于多因子模型构建互换利差交易策略不可行。利用统计套利方法检验反转策略和动量策略应用于5年期互换利差的效果显示：若不考虑交易成本，反转策略有效而动量策略失效; 然而互换利差的反转效应较弱， 盈利不足以弥补交易成本。因此，统计策略方法亦不可行。

第二，在纵向策略方面，本文观察互换利差期限结构的特点，利用利差曲线的骑乘特点，综合套利策略，设计了针对2年期互换利差的骑乘交易策略。骑乘策略若想获得较好回报，需要满足条件Ⅰ：收益率曲线较为陡峭和条件Ⅱ：策略执行期间利率没有上行。互换利差期限结构与国开债期限结构陡峭程度相似，而互换利差波动较小，利率上升风险较小，即互换利差对于条件Ⅰ的满足程度与国开债相似，且比国开债更可能符合条件Ⅱ的要求，因此由互换利差构建的骑乘策略比由国开债构建的骑乘策略更为稳定。

第三，多因子模型和统计套利模型应用于互换利差的效果并不好，两种方法均无法考虑市场中一些不可量化的主观因素对于互换利差的影响。然而很多情况下，正是这些不可量化因素导致了互换利差的变动。企业的公司金融因素、投资者对于未来宏观经济和利率走势的预期等多重因素决定了利率互换的供给和需求，然而这些因素难以用量化指标衡量（多因子模型失效），且无法从历史数据中获得（统计套利方法失效）。因此本文认为，若针对某一期限的互换利差，投资者基于市场基本面，对互换利差的供需关系和未来走势进行主观判断是最适用于互换利差的交易策略。此外，投资者可以将互换利差作为相对价值的观测指标。即基于基本面观点，结合利差大小，选择要介入的品种。实证结果肯定了将骑乘策略应用于互换利差的效果，然而在真实交易中，策略涉及的因素比较复杂，投资者的主观判断、 交易开仓频率等因素均会影响策略效果，因此实证结果的参考价值有限，本文仅提供一个大致的策略框架。

第四，通过理论分析和实证检验，本文为投资者投资于互换利差提供了理论和数据支持。 然而，真实的债券市场缤纷错杂，尤其是对于互换利差这一交易品种，众多不可量化因素决定了市场供需关系，仅凭历史数据制定的静态交易策略无法完美拟合市场走势，根据市场基本面状况及互换市场发展情况，进行全面透彻分析，制定动态交易策略才是投资之道。因此，本文的目的并不在于给予投资者具体的投资策略，而是针对互换利差，为投资者展示一个切实可行并可以长期应用的思维框架。

参考文献：

[1]HE H.Modeling Term Structures of Swap Spreads[R].Yale School of Management Working Papers，2000，3.

[2]LEKKOS I，MILAS C.Identifying the Factors that Affect Interest Rate Swap Spreads[J].Journal of Futures Markets 2001，21（8）： 737-768.

[3]HUI C H，LAM L.What Drives Hong Kong Dollar Swap Spreads：Credit or Liquidity？[J].Working Papers，2008（2）.

[4]杨辉，韩冬.互换利差特征与影响因素——基于人民币利率互换市场的研究[J].中国货币市场，2008（1）：18-23.

[5]程昊，李鹤然.无套利框架下互换利差影响因素分析[J].金融市场研究，2018（9）：50-62.

[6]FELDH？譈TTER P，LANDO D.Decomposing Swap Spreads[J].Journal of Financial Economics，2008，88（2）：375-405.

[7]FEHLE F.The Components of Interest Rate Swap Spreads： Theory and International Evidence[J].Journal of Futures Markets：Futures，Options，and Other Derivative Products，2003，23（4）：347-387.

[8]张戡，李小兰.利率互换套利交易模式及其影响因素研究——基于我国银行间同业拆放利率[J].金融理论探索，2016（1）：5-11.

[9]CHUNG H L，CHAN W S.Impact of Credit Spreads，Monetary Policy and Convergence Trading on Swap Spreads[J].International Review of Financial Analysis，2010，19（2）：118-126.

[10]LEKKOS I，MILAS C.Common Risk Factors in the U.S.and UK Interest Rate Swap Markets：Evidence From a Nonlinear Vector Autoregression Approach[J].Journal of Futures Markets：Futures，Options，and Other Derivative Products，2004，24（3）：221-250.

[11]SORENSEN E H，BOLLIER T F.Pricing Swap Default Risk[J].Financial Analysts Journal，1994，50（3）：23-33.

[12]袁志輝.骑乘策略在中国债券市场的应用探讨[J].债券，2018（4）：42-48.