浅谈数形结合在高年级教学中的应用

陈曙平

[摘 要]在小学数学的教学过程中，教师可以根据教学内容的特点，适当引入数形结合来帮助学生理解相应的知识。将代数知识与几何图形有效结合，可以巧妙地解决数学中的很多难题，还可以激发学生的学习兴趣，帮助学生深入理解所学内容，从而实现高效学习。

[关键词]小学高段;数学教学;数形结合

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2020）05-0042-02

现如今，无论是教师还是家长，都在寻找可以使学生高效学习的方法，笔者也不例外。想要帮助学生找到高效的学习方法，教师就必须深入研究教学，找到一些讲题技巧。下文中，笔者从3个方面谈一谈数形结合在小学高年级数学教学中的应用，分享有助于学生高效学习的方法。

一、通过数形结合掌握计算方法

计算在小学数学中占了很大一部分，然而在小学数学高年级的教学中，很多教师忽略了算理的重要性，导致部分学生计算能力不过关。教学过程中，教师不仅要教授学生计算的方法，还要让学生经历算理形成的过程，这样才能让学生深刻理解相应算理的具体含义，形成扎实的计算技能。

例如，小学五、六年级的学生经常会遇到这样的计算题：[12]+[14]+[18]+[116]。学生都知道可以用“首项×2-末项”这个公式计算，但是在具体计算时经常会出现计算错误。究其原因，是学生没有真正明白这个公式包含的算理。因此笔者将此类题目与图形相结合，以数形结合的方式进行教学。

为了增加题目的趣味性，笔者设计了一个情境：“现在有一堆沙子，我第一天装了一个箱子的[12]，第二天装了这个箱子的[14]，第三天装了这个箱子的[18]，第四天装了这个箱子的[116]，请问我一共装了这个箱子的几分之几？”在叙述的过程中，笔者画出图1，这样学生不仅明白了算理，还知道了这个算式是如何形成的，深化了理解。本题是把分数转化为图形，数与形巧妙结合，使得学生很容易就能发现其中的规律：如果前一个分数是后一个分数的2倍，这样一组分数的和，就等于第一个分数的2倍减去最后一个分数。

二、通过数形结合理解数量关系

接触过新版北师大版小学数学教材的教师都知道，新教材的特点是重视数学知识与生活实际之间的联系，而这有利也有弊。新教材與旧教材相比，淡化了问题解决和数量之间的关系，这对学生来说无疑增加了难度。因此，在教学过程中，教师需要巧妙地利用数形结合的思想，帮助和引导学生整理题目中的数量关系，从而对题目形成更深层次的理解，提高解决问题的效度。

例如，在给学生拓展和差问题的时候，笔者补充了一道题目：“波利老师像我（多利）现在这么大时，我才4岁;当我像波利老师现在这么大时，老师就28岁了。你知道我现在多少岁吗？”

师：同学们先独立思考2分钟，然后小组讨论3分钟，看看这道题目该怎么解决呢？

师：同学们，这是一个什么问题？

生（齐）：年龄问题。

师：在年龄问题中，什么是始终不变的？

生（齐）：年龄差。

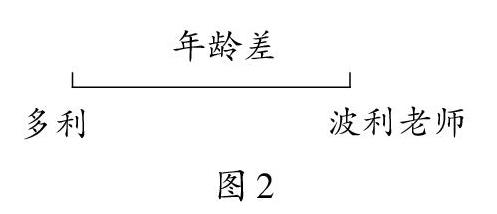
师：为了方便理解，我们利用一个线段图（如图2）来表示，线段左端点表示多利今年的年龄，线段右端点表示波利老师今年的年龄，线段长度表示两人的年龄差。

师：思考一下，要在这个线段图中表示出“波利老师像我现在这么大时，我才4岁”，可以怎么画？

师：以图2的线段为基准，对于“波利老师像我现在这么大时，我才4岁”，我们可以在图2下方增加一条表示年龄差的线段（长度同图2，用虚线画，如图3），将线段的右端点与多利今年年龄对齐。仿照这个做法，还可以在这个线段图中表示出“当我像波利老师现在这么大时，老师就28岁了”（如图3中右侧虚线）。

师：从图3中，你能得到什么信息？

生1：多利4岁和波利老师28岁相差了3个年龄差，可以计算出1个年龄差是多少。

师：那么多利今年的年龄该如何计算呢？

学生本来对这道题无从下手，但经过笔者的引导，学生慢慢有了方向。其中，真正帮助学生深入理解的是图3，它让学生厘清了4岁和28岁之间的关系，从而顺利解答此题。

三、通过数形结合发展数学思维

数形结合可以帮助学生有效解题，更能培养学生的数学思维。由于单纯的数学与数学运算大多都是抽象的，而小学生的抽象思维能力较弱，形象思维能力相对较强，因此，教师在教学中可以将“数”与“形”相互转化，找到适合小学生的学习方式。

例如，教学“平均数”时，笔者补充了一道题目：“学校组织跳绳比赛，10名选手按跳绳成绩从高到低排序，排名靠后的4名选手被淘汰。这时余下选手的平均成绩比10名选手的平均成绩高2分。那么淘汰的4名选手的平均成绩比10名选手的平均成绩少多少分？”以下是部分教学环节展示。

师：从题干中你能获取哪些有用信息？

生1：前6名选手的平均成绩比10名选手的平均成绩高2分。

师：所求问题是什么？

生2：后4名选手的平均成绩比10名选手的平均成绩少多少分。

师：这样看题目已知信息少，单个选手的成绩以及平均成绩都是未知的。我们应该从哪里下手呢？

生3：找不变量。

师：对！那么这道题的不变量是什么呢？

生4：10名选手的总成绩。前6名选手的总成绩+后4名选手的总成绩=10名选手的总成绩。

师：依次说说这里每一个总成绩如何表示？尝试将它与已知信息相联系。

生5：前6名选手的总成绩=前6名选手的平均成绩×6，后4名选手的总成绩=后4名选手的平均成绩×4，10名选手的总成绩=10名选手的平均成绩×10。

师：能不能借助图形来表示数据呢？

师：根据几人的平均成绩×人数=几人的总成绩，可以利用长和宽分别表示人数和平均成绩，那么面积就表示总成绩。

师：你能画出图形吗？

生6：以10名选手的平均成绩为宽，人数10为长，构造长方形ABCO，这个长方形的面积就是这10名选手的总成绩。前6名选手的平均成绩比10名选手的平均成绩高2分，即将宽增加2，长缩小4构造长方形DEFO，这个长方形的面积就是前6名选手的总成绩。假设后4名选手的平均成绩为G，那么长方形GHCF的面积就是后4名选手的总成绩。

师：根据前面的分析，可以得到哪些结论？

生7：（1）长方形DEFO的面积+长方形GHCF的面积=长方形ABCO的面积;（2）甲处面积=乙处面积;（3）后4名选手的平均成绩比10名选手的平均成绩少的部分是2×6=12（分），所以后4名选手的平均成绩比10名选手的平均成绩少12÷4=3（分）。

以上教学过程，教师通过构造长方形面积表示数量变化，可以从较少的题干信息中转化出新的信息，便于解决问题。

总之，在教学过程中，我们要深入研究教材，深度挖掘隐藏知识背后的数学思想，将数形结合落到实处，丰富学生的思维活动，为学生的终身学习打好基础。

（责编 李琪琦）