正交偏振双色激光场作用下高次谐波的椭偏特性研究

张 军，刘学深

（吉林大学原子与分子物理研究所，长春 130012）

1 引言

极紫外（XUV）光谱范围内的椭圆偏振阿秒脉冲在阿秒科学中有着非常重要的应用［1，2］，引起了研究人员极大的研究兴趣.随着激光技术的飞快发展，强激光与原子、分子相互作用获得了广泛关注，例如：高次谐波发射、阈上电离、隧穿电离、多光子电离、库仑爆炸等［3-6］.高次谐波理论有广泛的应用，例如产生相干阿秒脉冲和探测超快动力学，这其中，由于高次谐波具有平台区等特性，使其成为获得孤立阿秒脉冲的有效手段之一.时间尺度极小的阿秒脉冲可以用来探测原子及分子内部电子运动过程，对电子动力学研究起到了重要的作用［7-9］.对于高次谐波的理论解释有很多，其中1993 年Corkum等人［10］首次提出的半经典三步模型得到了广泛认同：首先，激光与原子分子相互作用时原子势垒的一侧被压得很低，使得处于基态的电子通过隧穿电离或多光子电离跃迁到连续态；其次，跃迁到连续态上的电子在激光场中加速并获得额外的动能；最后当激光场反向时，电子在激光场中减速直到速度减为零，部分电子反向加速返回到母核附近与母核复合并释放出高能光子，产生高次谐波.

近年来，分子高次谐波的研究因其在探索复杂分子结构中的应用而成为焦点话题［11-13］.分子高次谐波的一个特殊部分是来自不同原子中心贡献之间的干涉现象，这一现象受到了广泛关注.Lein等人［14，15］理论上研究了玻恩奥本海默近似下，激光偏振方向与分子轴之间夹角的变化会引起谐波强度上的变化，结果表明干涉效应的产生会引起H2+分子的谐波谱强度出现极大值和极小值.由于分子核间的双中心干涉和不同复合电子轨迹间的干涉现象，可以导致一些谐波阶次强度的异常增强或抑制［16］.谐波强度极小值的出现依赖于分子间的干涉效应、激光载波包络相位［17］以及不同的分子间核间距的变化［18］，这些因素可以导致谐波强度极小值位置的改变.此外，分子基态与激发态之间的干涉也可以影响谐波强度极值位置的变化［19］.最近Hu等人［20］利用密度泛函理论研究了CO分子的奇、偶次谐波的偏振方向，发现奇次谐波的偏振方向与驱动场的偏振方向相同，而偶次谐波的偏振方向与分子轴方向相同，这与先前对于奇偶次谐波具有相同的偏振方向的结论有所不同.实验上发现线偏振驱动场与分子相互作用可以产生椭圆偏振的高次谐波［21］.Son等人［22］研究了任意取向角下H2+分子谐波的振幅、相位以及偏振态等特性，发现高椭偏率的出现依赖于分子轨道对称性和双中心干涉效应，这一发现适用于一般情况下的准直线性分子.由此，谐波椭偏率的研究逐渐成为热点［23-26］.

通过引入正交偏振场的二次谐波场可以更好地控制谐波的产生，使得电子轨迹发生横向偏移.利用正交偏振双色场可以引导离子核附近具有阿秒精度的隧穿电子，从可调的方向以阿秒分辨率探测离子波包动力学，为利用高次谐波辐射产生阿秒脉冲提供了新的途径［27］.当二次谐波场相对较弱时，基频场决定了高次谐波的时频，通过观测和分析两个场之间的延迟，可以重建电离与重碰时刻［28］.在由基频场和有时间延迟的较弱二次谐波场组成的正交偏振双色场中，不对称分子的高次谐波有明显的取向依赖性，干涉效应只在分子的一侧可见［29］.

本文通过求解二维含时薛定谔方程研究了正交偏振双色激光场下H2+分子的高次谐波发射以及阿秒脉冲的产生.计算结果表明，激光场强度比的变化可以调控谐波强度以及两个方向上所产生的奇偶次谐波的椭偏率.随着激光场强度比的增加，y方向上的谐波强度不断提高.当场强比为1：2.5 时发现x、y方向上分别只有奇次谐波、偶次谐波产生，奇次谐波的椭偏率可以达到0.3，偶次谐波的椭偏率接近于0.此外，改变分子准直角也可以调控谐波的椭偏率，利用椭圆偏振高次谐波的平台区可以合成椭圆偏振阿秒脉冲链.

2 理论模型

我们通过数值求解二维含时薛定谔方程（TDSE）研究了H2+分子的高次谐波发射.2DTDSE写成如下形式（在原子单位下）

其中θ为分子轴与x轴之间的夹角，R=2 a.u.是核间距，a=0.735 为软核参数，对应的H2+的电离势为Ip=1.09 a.u.［26］.通过求解TDSE，利用虚时演化的方法构造初始波函数.外部电场为正交偏振双色场，它是由基频场Ex（t）和二倍频场Ey（t）组成.其表达式为为激光场的峰值强度，ω0是基频场的频率.激光脉冲采取的是具有3 个光学周期的梯形包络，其中上升沿、下降沿和平台区均为1 个光学周期.通过二阶分裂算符的方法［30］计算含时波函数，所用到的空间步长为0.4 a.u.，时间步长为0.05 a.u.，空间网格为409.6 a.u..为了抑制边界反射，使用了面具函数，其表达形式为

根据埃伦费斯特理论，偶极加速度的表达式可写成［31］

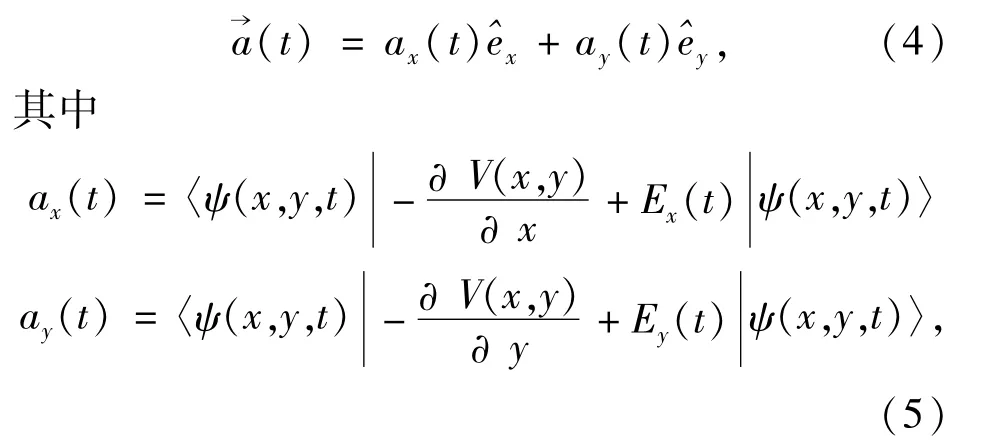
高次谐波谱的强度正比于→a（t）的傅里叶变换模的平方

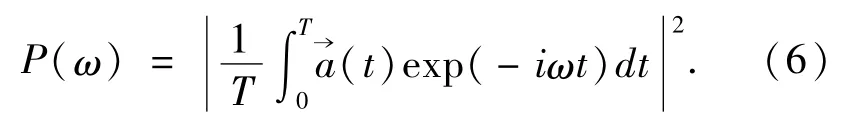
高次谐波椭偏率的表达式为

3 结果与讨论

本文研究了正交偏振双色激光场与H2+分子的相互作用，所选x方向的激光场强度为5 ×1013W/cm2，激光频率为0.043 a.u..图1 展示了由x方向激光电场和不同激光场强度比下y方向二次谐波场随时间的变化.黑色实线表示基频场，红、蓝、紫、绿色虚线分别表示激光场强度比为0.1、1.0、1.6、2.5 情况下的倍频场.我们发现随着激光场强度比的增大，倍频场峰值强度逐渐增大.

图1 正交偏振双色场示意图.黑色实线表示x方向的激光电场，红色、蓝色、紫色、绿色虚线分别表示激光场强度比γ为0.1、1.0、1.6、2.5时y方向的二次谐波场.其中，x方向的激光强度为5 ×1013 W/cm2，激光频率为0.043 a.u..Fig.1 The diagram of OTClaser field.The black solid line represents the laser field in the x direction，the red，blue，purple and green dotted lines represent the second harmonic field in the y direction where the laser intensity ratios are 0.1，1.0，1.6 and 2.5.The laser intensity in the xdirection is 5 ×1013 W/cm2 and the laser frequency is 0.043 a.u..

图2（a）-2（d）展示了不同激光强度对高次谐波发射的影响，对应的准直角为0 度.其中，x方向和y方向的谐波谱分别用红色和黑色线条表示.当γ=0.1 时，从图2（a）我们可以看出x方向的高次谐波强度要高于y方向的谐波强度，这可以通过x方向的电场强度较大来解释.随着场强比的增加，y方向的谐波强度不断提高.当γ=2.5时，x方向的谐波强度与y方向的谐波强度相比，会有两到三个数量级的下降.同时，y方向（垂直于分子轴的方向）产生偶次谐波，而x方向（平行于分子轴的方向）产生奇次谐波，如图2（d）中的插图所示.

图2 正交偏振双色激光场中，不同激光强度比下H2+分子的高次谐波的产生.红色和黑色的线分别表示x，y两个分量的高次谐波.其中，激光场的强度比分别为（a）γ=0.1，（b）γ=1.0，（c）γ=1.6，（d）γ=2.5.图（d）中的插图为20th-40th阶次的谐波.对应的准直角为0度.Fig.2 The HHG of H2+molecule with different laser intensity ratios in the OTC laser field.The red and black lines represent the HHG of x and y components，respectively.The laser intensity ratios are（a）γ=0.1，（b）γ=1.0，（c）γ=1.6，（d）γ=2.5，respectively.The inset in（d）shows the HHG spectra from 20th to 40th harmonic.

图3 显示了不同激光强度比下不同谐波阶次的椭偏率.当强度比γ=0.1 时，在20 -30th 阶次之间谐波的椭偏率较大，最大值可以达到0.34.在30 -40th阶次之间，谐波的椭偏率较小.对于谐波椭偏率的变化我们可以通过图2（a）中的谐波谱来理解，在30th阶次之前x，y方向的谐波强度相当，谐波近似为圆谐波，从而导致椭偏率较大.当30th阶次之后，x方向的谐波强度明显要强于y方向的谐波强度，对应的谐波椭偏率较小.当γ=1.0和γ=1.6时，30 -40th阶次之间的椭偏率要大于20 -30th 阶次之间，这与图2（b）和2（c）中随着阶次的增加，x，y方向谐波的强度差逐渐减小相符合.当γ=2.5 时，在整个光谱中奇次谐波比偶次谐波的椭偏率大，y方向的激光场强度比较大相符合.我们还可以看出，当激光场的强度比相等即γ=1.0 时，在40th 阶次时我们可以得到谐波椭偏率的最大值.

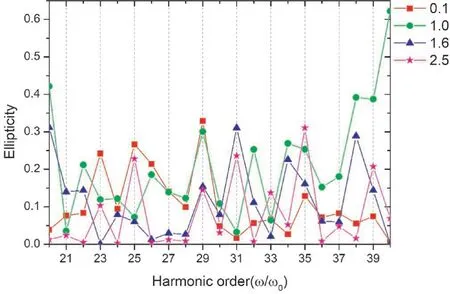
图3 正交偏振双色场中，不同激光强度比下高次谐波的椭偏率.其中，x方向的激光强度为5×1013 W/cm2，激光场的强度比分别为γ=0.1，γ=1.0，γ=1.6，γ=2.5.对应的准直角为0度.Fig.3 The ellipticity of HHG with different laser intensity ratios in the OTC laser field.The laser intensity in the x direction is 5 ×1013 W/cm2，the laser intensity ratios areγ=0.1，γ=1.0，γ=1.6 and γ=2.5，respectively.

图4（a）和4（b）分别展示了场强比为2.5 时的偶次谐波和奇次谐波的椭偏率随准直角度的变化.从图4（a）中我们可以看出当准直角为0 度时，偶次谐波的椭偏率很小.同时，准直角的变化对谐波椭偏率的影响很大，使得高次谐波在左圆偏振、线性偏振和右圆偏振之间发生转换.我们还可以看出不同阶次的偶次谐波的椭偏率变化趋势是比较一致的，在30 度、72 度和114 度左右时椭偏率存在拐点.对于30th 阶次和32th 阶次，分别在117 度和72 度左右椭偏率可以达到极大值.在图4（b）中我们能够看到当准直角为0 度时，不同阶次的奇次谐波的椭偏率是不同的，这与图3 中椭偏率主要出现在奇次谐波位置是符合的.随着准直角的增加，奇次谐波椭偏率的变化趋势比较杂乱.对于35th 阶次，在72 度左右时椭偏率达到极大值.

图4 场强比γ=2.5时，不同准直角下高次谐波的椭偏率.（a）和（b）分别对应偶次谐波和奇次谐波.Fig.4 The ellipticity of HHG with different alignment angles，when the laser intensity ratio isγ=2.5.（a）and（b）correspond to the even and odd order harmonics，respectively.

图5 正交偏振双色场下叠加30th到40th阶次谐波合成的阿秒脉冲，（a）和（b）对应的准直角分别为18°和72°.Fig.5 Attosecond pulse synthesized by superposing 30th to 40th harmonics under the OTC laser field，（a）and（b）correspond to the alignment angles are 18°and 72°，respectively.

通过上图的分析我们可以看出，偶次谐波的椭偏率变化趋势是比较一致的，而奇次谐波的椭偏率分布是比较无规律的.因此，接下来我们主要分析一下谐波为奇数阶次时椭偏率的情况.我们发现，在准直角为18°时奇次谐波的椭偏率分布比较集中，椭偏率之间相差不大.相反，在准直角为72°时椭偏率分布是不规律的，不同阶次之间椭偏率相差的比较大，尤其是35th 阶次相差的更大.于是，我们主要分析这两个角度，并对这两个角度条件下合成的阿秒脉冲进行比较，如图5（a）和5（b）所示.图5（a）和5（b）分别给出了在准直角分别为18°和72°时，通过叠加30 到40th阶次谐波合成的阿秒脉冲.从图5（a）中我们能够发现，准直角为18°时产生了两个相对孤立的阿秒脉冲.从图5（b）中可以看出，在准直角为72°时产生了很多子脉冲，无法形成孤立的阿秒脉冲.由此可以说明椭偏率比较相近时更有利于合成孤立的阿秒脉冲.同时，我们也计算了在这两个角度时阿秒脉冲的椭偏率，我们得到，在准直角为18°时阿秒脉冲椭偏率为0.05 以及72°时椭偏率为0.8.也就是说，在准直角为18°时各阶次椭偏率相近，可以合成几乎是椭圆偏振的阿秒脉冲.

4 结论

本文理论研究了正交偏振双色场驱动下的二维H2+分子的高次谐波发射和阿秒脉冲的产生.研究结果表明，提高二倍频与基频场的场强比，y方向的谐波强度不断提高.并且我们发现偶次谐波和奇次谐波都具有很高的椭偏率.当场强比γ=2.5时，偶次谐波的效率比奇次谐波的效率高2-3 个数量级，并且奇次谐波的椭偏率最大可以达到0.3.此外，通过调整分子的准直角度，可以对谐波的椭偏率进行控制，使其在左圆、线性和右圆偏振之间转换.基于这一现象，利用椭圆偏振HHG的平台区合成了椭偏率为0.05 的椭圆偏振阿秒脉冲链.