F+HD→DF+H在中等碰撞能量下的反应立体动力学研究
王晓驰,解廷献
(1.大连交通大学机械工程学院,大连 116028;2.大连交通大学理学院,大连 116028)
1 引言
F+H2→HF+H及其同位素反应是非常经典的放热反应[1-7],作为最重要的一个同位素反应,F+HD收到广泛的关注,科学家从实验和理论两方面对这个体系进行了大量研究[8-11].2000年刘国平等使用交叉分子束方法测量了F+HD反应的两个通道的反应截面,发现了该反应的许多共振特性[12-14].这些研究成果促进了对该体系的理论研究[10,11,15,16].
从动力学计算角度讲,势能面对于理解反应机制非常重要,在1971 年Muckerman 构建了F+H2的半经验势能面(M5)[17].F+H2→HF+H第一个高精度的势能面由Stark 和Werner构建的(SW势能面),这个势能面是通过拟合从头算数据得到的[18],随后在这个势能面上进行了大量的理论计算[19-22].由于SW势能面没有考虑自旋与轨道耦合相互作用,所以Alexander等考虑自旋与轨道耦合相互作用拟合了一个新的势能面(ASW势能面)[7],本文的计算就是在ASW势能面上进行的.
对一个体系的反应而言,它的标量属性很重要,在某些情况下他的反应矢量性质同样起着重要的作用.杨学明等在2001 年使用交叉分子束技术测量了F+HD几个能量点的反应的立体动力学特性[23].虽然对F+HD体系进行了大量的理论计算,但是到现在为止还没有看到关于这个实验测量的在碰撞能3.987 Kcal/mol时F+HD反应立体动力学特性的理论计算.为了便于和实验数据比较,我们计算了碰撞能为3.987 Kcal/mol时F+HD→DF+H反应的立体动力学性质.准经典轨线(QCT)是一种研究反应体系矢量性质的有效方法,这种方法物理概念清晰,计算量少,多年来得到人们的广泛应用[24,25],本文采用准经典轨线方法研究F+HD→DF+H反应的立体动力学性质.
2 理论方法
QCT详细描述参见文献[26-30].我们选用质心坐标系如图1,z轴平行于反应物相对速度k,y轴垂直于含有反应物相对速度k 和产物相对速度k'的xz平面.

图1 质心坐标系下描述k,k'和j'相关图.Fig.1 The center-of-mass coordinate system used to describe the k,k'and j'correlations.
本文采用准经典轨线方法对反应物分子转动量子数为j=0,1,2 时进行了详细的立体动力学研究,反应物的相对速度k与产物的转动角动量j'的夹角θr从0°到180°.描述反应物相对速度k、产物相对速度k'和产物的转动角动量j'三矢量相关性质的角φr的范围覆盖0°到360°,反应中FHD距离选为10 Å积分步长为0.1 fs,运行轨线50000 条使该反应得到了较好的收敛.
相应的矢量相关函数p(θr),p(φr)由下面公式定义[31-34].在质心坐标系下,描述三原子反应中两矢量相关的分布函数p(θr)可以展开为一系列的Legendre多项式

描述三矢量相关的函数p(φr)可以用傅里叶级数展开
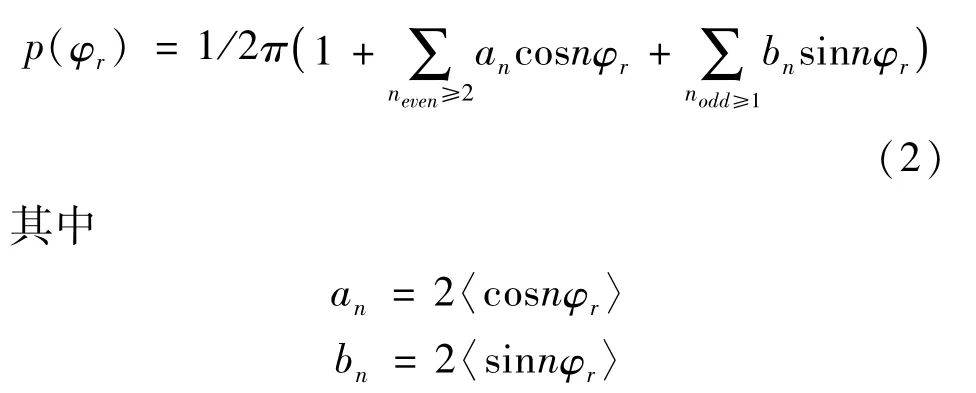
描述k、k'、j'三矢量的全三维角分布函数写为:

3 结果与讨论
极化微分反应截面(2π/σ)(dσ00/dσωt)对应实验可以测量的微分散射截面(DCS),图2 给出了我们QCT的计算结果和实验结果[23].实验测量的微分散射截面是相对值,理论可以乘以系数和实验数据比较,通过图2 可以看出理论和实验的结果的趋势基本一致,在小角度时产物基本为零,产物集中在大角度,现出比较强的前向散射.产物振动态分布主要集中v'=2,3,在大角度都有峰值.我们的计算结果与实验结果的在峰值的位置上有较大差别,理论的峰值位置比实验的峰值位置小15o左右,例如总的散射截面实验峰值在135o,理论计算结果在121o.其次产物v'=1 微分散射截面与实验的差别比较大,实验上v'=1 的微分散射截面非常小,我们的计算结果偏大.可能是由于ASW势能面的势垒偏高,在ASW势能面上计算的F+HD→HF+D通道的共振位置与实验相比向高能偏移了0.346 Kcal/mol[15].
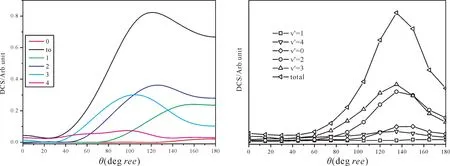
图2 反应物DF+H在不同振动量子数的微分散射截面,左边为QCT结果,右边为实验结果[23].Fig.2 Differential cross sectionsof the reagent vibrational quantum numbers,QCT results(left),Experimental data(right)[23].
我们给出了反应转动量子数分别为0 -2 时的反应物相对速度矢量k 和产物的转动角动量矢量j'两矢量相关的函P(θr)分布,P(θr)的分布直接反映了k,j'的两矢量相关.从图3 可以很清晰地看出,P(θr)分布的峰值均位于θr=90°,同时每一个反应都关于θr=90°对称.随着反应物转动量子数的增加,峰值越来越小,半高宽变宽表明反应的产物的转动角动量的取向性减弱.

图3 反应物在不同转动态时k-j'相关的p(θr)分布图Fig.3 The distributions of p(θr)reflecting k-j'correlations at different rotational levels j=0 -2 for the reagent rotational excitation.
反应产物的方位角p(φr)分布是描述三矢量相关k-k'-j'[35-37],结果如图4 所示.从图4中可以看出,p(φr)关于φr=180°是非对称的,说明标题反应产物角动量具有强烈的极化,在φr=270°峰值表明产物转动角动量j'在y轴负方向有强烈的定向效应.P(φr)随着产物转动量子数的增加,峰值越来越小,表明反应的产物的角动量的定向性减弱.
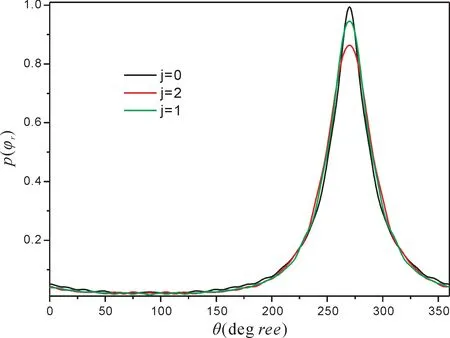
图4 反应物在不同转动态时相应于k-k'-j'平面的p(φr)分布图Fig.4 The dihedral angle distribution of p(φr)with respect to the k-k'-j'plane plotted at reagent rotational quantum numbers.
为了更深理解p(φr)分布的这种特点,必须考虑到产物更多的转动取向及定向效应.根据A+BC→AB+C分子反应的排斥模型[32,33],矢量j',有公式j'=L sin2β +j cos2β +J1mA/mB,L是反应物的轨道角动量,J1=(uBCR)1/2(rAB·rCB),uBC是B,C分子的约化质量,R是排斥能.在标题反应中,L sin2β +j cos2β是对称的,而J1mA/mB更容易受到排斥能的影响,倾向于某一方向,从而导致了产物具有定向效应趋势的原因[38-45].
4 结论
基于ASW基态势能面,采用准经典轨线方法,对反应F+HD(j=0,1,2)→DF+H的立体动力学进行了研究,计算了反应物转动量子数分别为0,1,2 时的极化微分反应截面,两矢量相关分布p(θr)以及三矢量相关分布p(φr).此外极化微分反应截面(2π/σ)(dσ00/dσωt)显示产物主要集中在大角度,小角度处产物分布非常小,验证了该反应的前向散射特性.随着反应物转动量子数增加,两矢量相关分布p(θr)峰值越来越低,半宽度变宽,取向程度逐渐减弱.三矢量相关分布p(φr)只有在2700时有峰值表明产物转动量子数j'定向于y轴负方向.
——《势能》

