第Ⅲ族元素磷化物热力学性质理论研究
吴杰,李嘉辉,于燕梅,于养信
(清华大学化工系化工热力学实验室,北京100084)
引 言
在过去几十年中,Ⅲ-Ⅴ族化合物因其独特的物理性质而在半导体材料领域受到广泛的研究和应用[1],其中第Ⅲ族磷化物半导体因为具备高热导率及独特的光电性质等优点,被广泛用于高温技术、新型电子产品及光催化等领域中,成为目前最具发展前景的材料之一[2-5]。
第Ⅲ族二元磷化物通常为闪锌矿结构[6],这一结构也是自然界最丰富的矿物资源之一。实验测定的BP、AlP、GaP 和InP 的熔点分别为1100、2000、1480、1070℃,说明其在高温下也能维持一定形状,而且除了InP 之外,均为间接带隙。具有直接带隙的InP 非常适合应用于将光电子与高速电子相结合的设备中,例如大直径的InP 基质已经成为推动光纤维通讯快速发展的重要材料,而且目前在太阳能电池中也有重要应用[7-8]。此外,Li等[9]最近发现BAs及BP 与Si、GaAs 等大多数常用于电子产品中的半导体在高温下有很小的晶格不匹配度,可有效降低材料间热应力,而且因其热导率高,是未来高能量电子产品的理想散热器。通过掺杂或功能化的AlP在气体传感器和新型电池中可以发挥重要作用[10-11],具有间接带隙的GaP 也在发光二极管、光电化学电极等光学领域占据重要地位[12-13]。由此可见第Ⅲ族元素磷化物作为一种新能源材料扮演着越来越重要的角色,对缓解和解决当前能源危机提供了一条十分有效的途径。为了充分发挥其潜能,许多研究开始制备第Ⅲ族三元磷化物从而不断改善其性能[14-16]。应用于高能量电子设备中的第Ⅲ族磷化物半导体材料,通常要面临高温条件,为了更好地开发这类磷化物半导体的应用,对于它们热力学性质的研究是十分必要的。
材料的热力学性质,如热容、自由能、热膨胀系数和熵等,通常与其弹性及力学等物理性质紧密相关,决定着材料在高温下的性能及存在形式[17-20]。目前许多理论和实验研究已经对第Ⅲ族元素磷化物的电子结构和光学性质做出了系统研究[1,5],但对于这类材料的热力学性质研究报道得较少。Daoud等[21]利用准谐Debye 模型详细研究了AlP 在0~2000 K 和0~10 GPa 范围内的熵、Debye 温度、热容等热力学性质,发现AlP 的热力学性质随着温度或压力做单调变化,而且一些计算结果与实验结果一致。Settouf 等[22]也在密度泛函理论框架下利用准谐近似Debye 模型分析比较BxAl1-xP 三元合金的热容和热膨胀系数,发现三元合金的等容热容更加接近Dulong-Petit 定律,而且可以通过改变x来调节金属磷化物的热膨胀系数,这也为今后磷化物的发展提供一条新途径。目前对于第Ⅲ族磷化物热力学性质还没有一个系统的研究,所以本文将通过第一性原理计算,利用声子模型详细计算比较BP、AlP、GaP、InP 的热容、自由能、熵、热膨胀系数等热力学性质,为第Ⅲ族磷化物在光电材料领域的研究和应用提供参考数据。
1 理论计算方法
1.1 结构优化理论及其参数设置
研究的BP、AlP、GaP 和InP 的空间群均为F-43m,结构为常见的闪锌矿结构,这一结构也是自然界最丰富的矿物资源之一。本文所有涉及的第一性原理计算都是利用CASTEP 模块[23]完成,而且使用的是包含自旋极化的密度泛函理论计算框架。使用OTFG 超软赝势[24]描述原子实和价电子之间的相互作用,交换关联能使用广义梯度近似下的Perdew-Burke-Ernzerhof(PBE)泛函[25],同时Grimme-D2方法[26]被用于考虑长程色散校正,其中B、Al、Ga、In 和P 元 素 的C6 参 数 分 别 为32.440、111.830、176.089、386.794、81.2559 eV·Å6,R0 参数分别为1.485、1.639、1.650、1.672、1.705 Å(1 Å=0.1 nm)。由图1 收敛性测试可知,为了平衡计算时间和计算精度,赝势截断半径可选为550 eV,在布里渊区选取的k点为8×8×8。此外,自洽场迭代中每个原子能量收敛值设为5.0×10-7eV,结构优化中力的收敛值为0.01 eV·Å-1,应力和位移的收敛值分别为0.02 GPa和5.0×10-2Å。
1.2 热力学性质计算
本文将首先通过CASTEP 中有限位移方法来计算得到磷化物单胞的声子态密度,然后利用式(1)~式(6)计算得到热容、熵等热力学性质[27]。等容热容的计算公式为
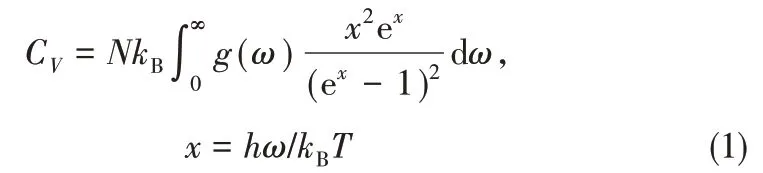
式 中,kB为Boltzmann 常 数;N为 自 由 度;h为Planck 常数;ω为声子频率;g(ω)为声子态密度;T为热力学温度。等压热容也可以在式(1)的基础上获得

式中,α为体积热膨胀系数,α=(1/V)(∂V/∂T);V为温度T下的体系平衡体积;B为相应体积模量。与温度相关的内能也可以借助式(3)由声子态密度计算获得。
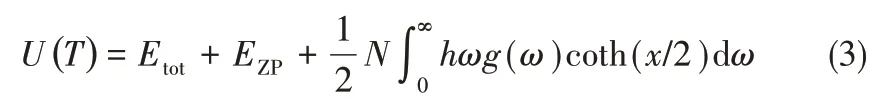
式中,Etot为由密度泛函理论计算得到的体系在0 K 时能量;EZP为由声子态密度计算得到的零点振动能。
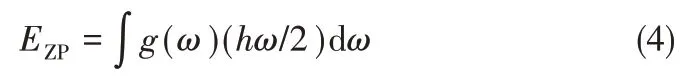
固体的熵S和Helmholtz 自由能F可利用式(5)和式(6)计算得到
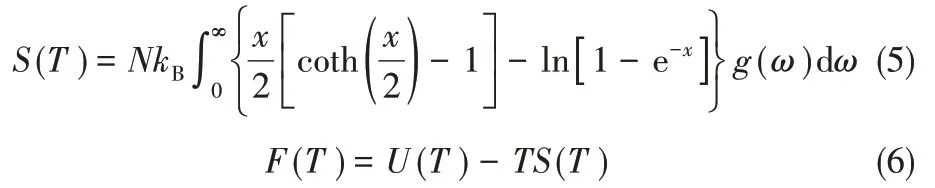
对于固体,与内能和Helmholtz 自由能相比,低压反应前后的Δ(PV)数值可以忽略不计,因此可以认为固体的内能U近似等于焓H,近似把Helmholtz自由能F当作Gibbs自由能G。
2 结果与讨论
2.1 结构性质
固体材料的形成本质上是原子间力相互作用的结果,而原子间的力又与材料的化学组成和晶格参数密切相关,所以结构性质的计算研究对于从微观角度理解材料性质是十分重要的。B、Al、Ga、In和P 原子的电子结构分别为[He]2s22p1、[Ne]3s23p1、[Ar]3d103s24p1、[Kr]4d105s25p1、[Ne]3s23p3,可以看到B、Al、Ga、In具有相同的价电子数,P的外层轨道具有5个价电子,但是由于原子质量以及原子半径的不同,从而造成在形成化合物时,空间价电子密度分布还是有所差异,这也就造成了键长以及晶格参数的不同。
图2 为0 K 时电子基态能量及零点振动能加和的相对值随晶胞体积的变化,通过能量对体积的一阶导数可以找到晶胞平衡体积及相应的结构性质。其结果总结列于表1,可以看到,B-P、Al-P、Ga-P 和In-P 键长分别为1.96、2.36、2.34、2.53 Å,基本呈现一个逐渐增加的趋势,这是因为一方面电负性B >P >Ga >In >Al,另一方面原子半径In >Ga >Al >B,故Ga和P的电负性差虽然较Al更小,即GaP的共价键成分更多,但由于原子半径也更大,两者键长相近;而In 和P 的电负性差虽然也较Al 更小,但是原子半径显著大于Al,所以InP 的键长要高于AlP。晶胞边长是固体材料最基本的结构性质之一,并且和键长直接相关。由表1 可知BP、AlP、GaP、InP 在0 K 的晶胞边长分别为4.530、5.449、5.422、5.848 Å,与化合物键长有着相同变化趋势,总体呈现逐渐增加的变化。此外,通过声子频率的计算可以获得晶胞在不同温度下的Gibbs 自由能及此温度下稳定结构,如300 K 时BP、AlP、GaP 和InP 的晶胞边长分别为4.531、5.450、5.427、5.850 Å。可以看到表1 中晶胞边长和体积模量的计算值与实验值及其他理论计算值的一致性很好,这也从侧面说明本文的计算参数设置比较合理。此外,还可以看到晶胞边长会随着温度升高而增大,说明金属磷化物可能属于热膨胀类材料。
2.2 热力学性质
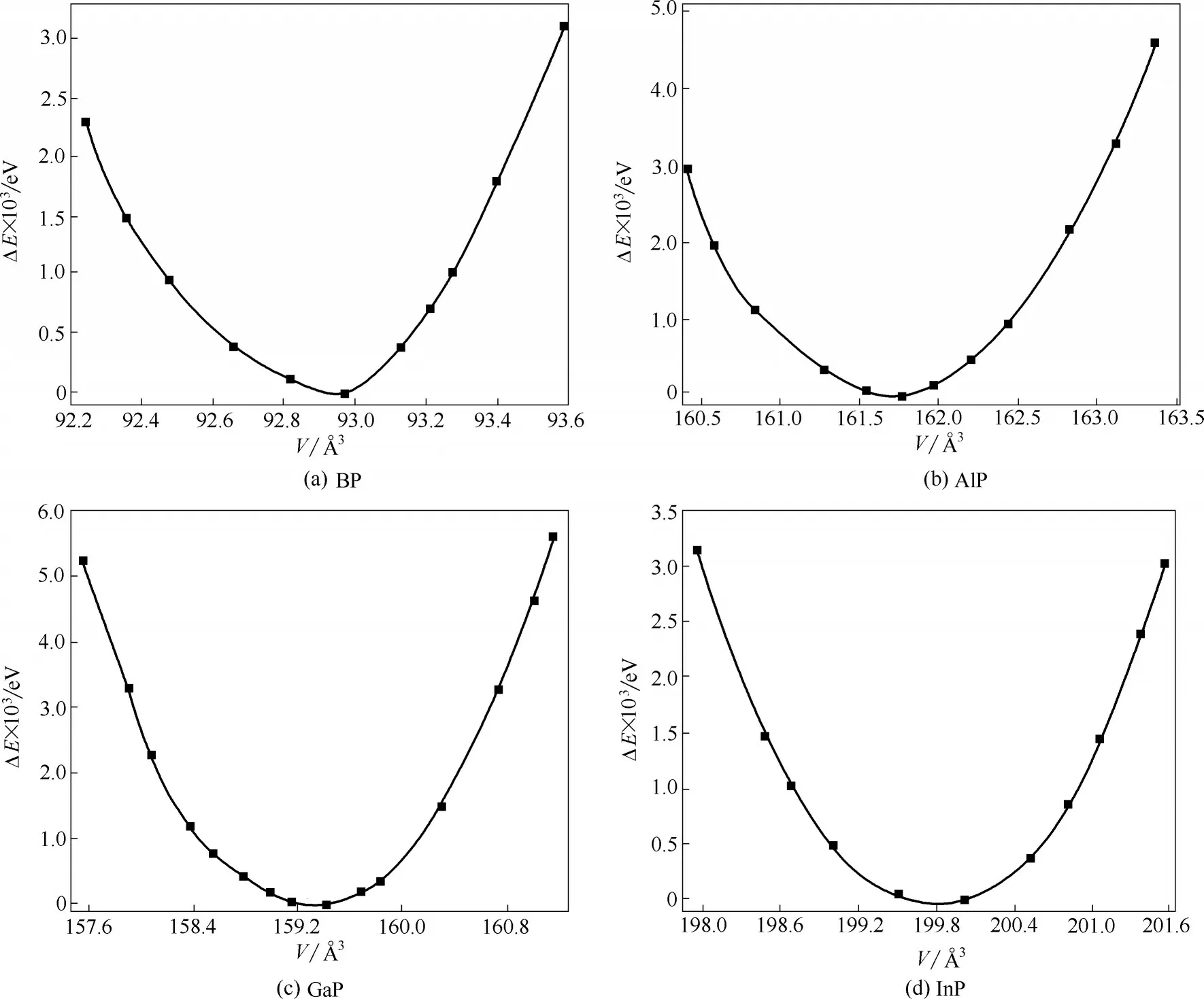
图2 第Ⅲ族元素磷化物的相对能量计算值(0 K)随体积变化曲线Fig.2 Calculated relative energy(0 K)for group Ⅲphosphides as a function of volume
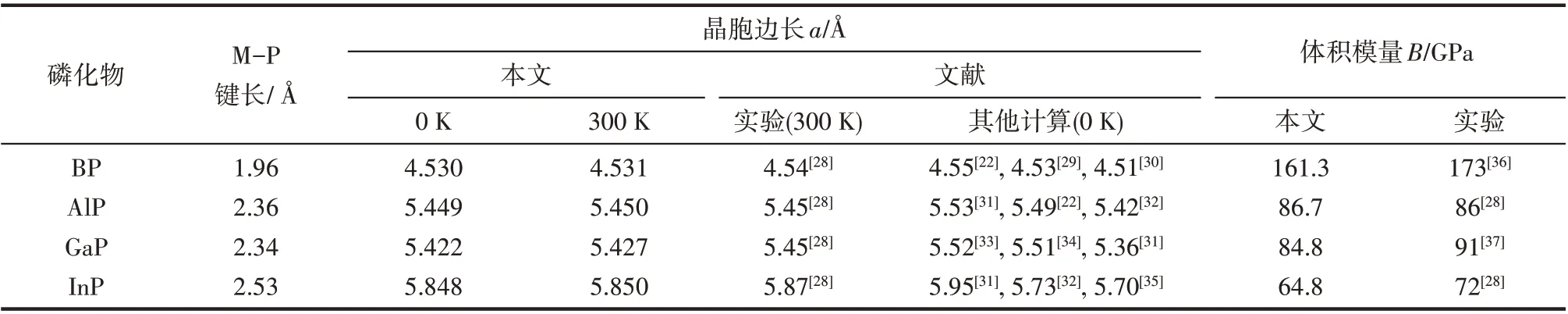
表1 闪锌矿结构金属磷化物的键长、晶胞边长和体积模量Table 1 Bond lengths,lattice constants a and bulk modulus for zinc-blende metal phosphides
对固体热容、熵、热膨胀系数等热力学性质的研究可以帮助研究者更好地理解材料在高温下所表现的性能、更充分地探索材料的应用潜能[21,38]。为了研究BP、AlP、GaP 和InP 的热力学性质,首先计算了它们单胞的声子色散曲线和声子态密度。图3为第Ⅲ族磷化物在理论平衡体积时的声子色散曲线,可以看到四种化合物在所有高对称点处均无虚频,这说明它们均具有动态稳定性,有助于材料在实际应用中的结构及性能稳定。此外,声子曲线中的声学分支和光学分支间存在一定带隙,这主要是因为磷原子和第Ⅲ族原子间存在质量差,而且由于第Ⅲ族磷化物的原胞中只有两个原子,所以总共有6 个振动模式在gamma高对称点处汇聚。
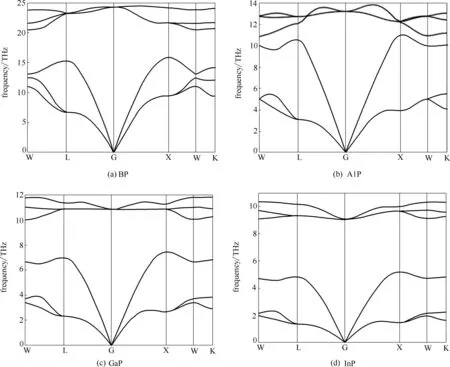
图3 第Ⅲ族元素磷化物在0 K时的声子色散曲线Fig.3 Calculated phonon dispersion curves for group Ⅲphosphides at 0 K
本文将在声子模型获得的声子态密度基础上,通过非简谐近似,利用式(1)~式(6)计算了相应热力学性质。图4 为BP、AlP、GaP 和InP 的焓值随温度变化的曲线,可以看到四种物质的焓值均随温度的升高而单调递增,但在低温时增速较慢,随着温度的升高曲线斜率也会显著提高,而且通过BP 和AlP的实验值[39]与本文计算值进行比较发现两者比较接近。图5为第Ⅲ族元素磷化物的熵值随温度变化曲线,可以看到在每一温度下均有InP 的熵值差最大,BP 的熵值差最小,且随着温度升高,熵值差先在低温下快速增加,然后会在高温时趋于平缓,这和焓的变化趋势相反。此外,图5 中还将本文计算值与文献实验值[39]进行比较,BP、AlP、GaP 和InP 在常温下计算值分别为20、42.3、52.3、66.4 J·(mol·K)-1,从图中可以看到AlP 和GaP 的计算值与实验值符合较好,而BP的计算值略低于实验值,InP的计算值略高于实验值,且随着温度升高这种差距稍有增加,这可能是因为实验材料中会存在空穴和其他晶格缺陷,从而造成一定的实验误差。总体而言,本文对于金属磷化物熵的计算值与实验值符合良好,说明理论计算是可靠的。
材料的热容CV是最重要的热力学参数之一,作为对声子密度的衡量,它不仅可以提供基质振动性质的本质信息,而且在许多应用中都有着重要影响[40],所以热容的研究对理解金属磷化物性质也是十分必要的。如图6 所示为BP、AlP、GaP 和InP 在一定体积下的热容计算值随温度变化曲线,它们具有相同的变化趋势,在低温下热容会随着温度升高呈现指数式增长,当温度上升到一定值时热容会趋于一个稳定值。可以看到当T>700 K 时,BP、AlP、GaP 和InP 的热容分别趋近于为47.0、49.0、49.2、49.3 J·(mol·K)-1,这和Dulong-Petit 极限值(CV=49.9 J·(mol·K)-1)非常接近,相同的定性变化行为也出现在AlN、NbN2等物质的研究中[40-42]。
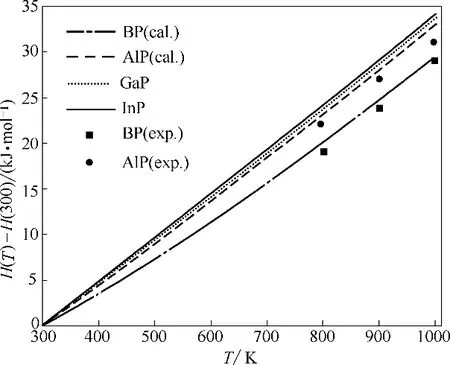
图4 BP、AlP、GaP和InP的焓随温度的变化(H(300)表示300 K时物质的焓)Fig.4 Calculated enthalpy as a function of temperature for BP,AlP,GaP and InP(H(300)is enthalpy at 300 K)
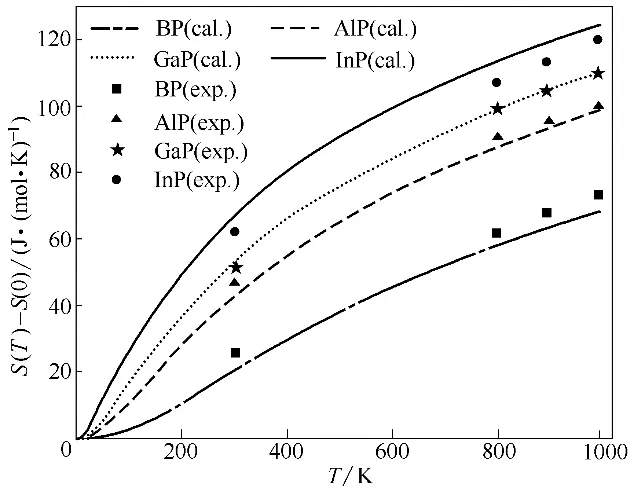
图5 BP、AlP、GaP和InP的熵随温度的变化(S(0)表示0 K时物质的熵)Fig.5 Calculated entropy as a function of temperature for BP,AlP,GaP and InP(S(0)is entropy at 0 K)
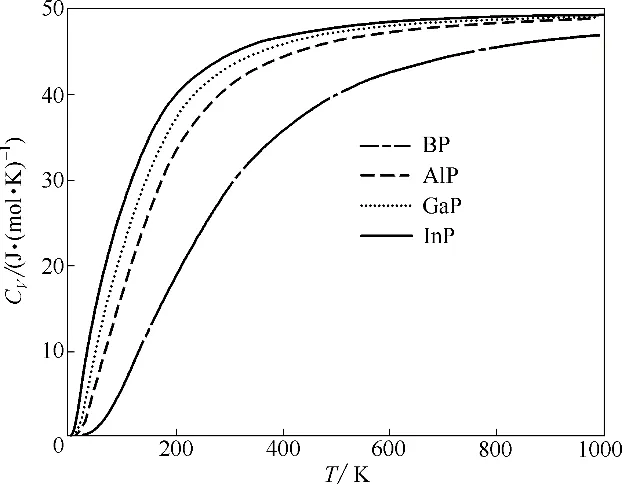
图6 BP、AlP、GaP和InP的计算热容随温度的变化Fig.6 Calculated heat capacity as a function of temperature for BP,AlP,GaP and InP
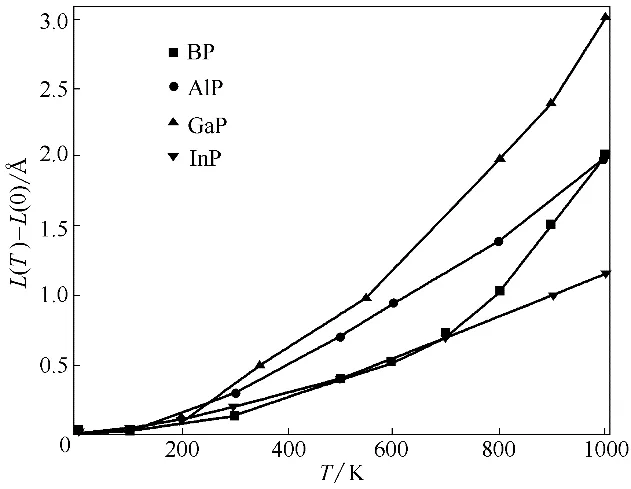
图7 BP、AlP、GaP和InP的平衡晶胞边长随温度的变化(L(0)表示0 K时晶胞平衡边长)Fig.7 Calculated equilibrium lattice parameter as a function of temperature for BP,AlP,GaP and InP(L(0)is equilibrium lattice parameter at 0 K)
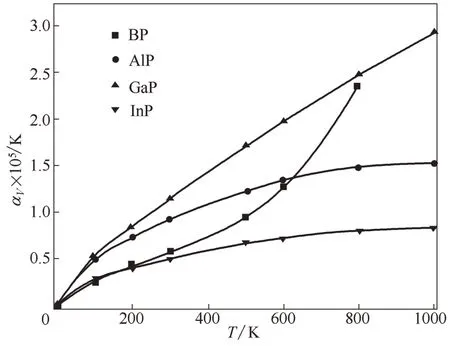
图8 BP、AlP、GaP和InP的体积热膨胀系数随温度的变化Fig.8 Calculated volume thermal-expansion coefficient as a function of temperature for BP,AlP,GaP and InP
热膨胀系数通常用于描述物体尺寸随着温度变化剧烈程度[43],这对于衡量高温下物体的工程实用性十分重要,因为两种物质的热膨胀系数相差很大时会在高温下产生很强的热应力,这对于系统稳定十分不利。在本文计算中,首先将晶胞压缩或膨胀到一系列体积,找到各个温度下的平衡体积,图7为BP、AlP、GaP 和InP 的平衡晶胞边长相对值随温度变化曲线,其中各个温度下的晶胞边长的大小次序为InP >AlP ≈GaP >BP,且随着温度升高各物质晶胞边长均有微小增大。由于体积热膨胀系数α为线性热膨胀系数[α=(1/L)(∂L/∂T)]的3 倍,所以在图7的基础上可获得BP、AlP、GaP 和InP 的体积热膨胀系数(图8)。由结构性质计算中的Hirshfeld 电荷可知BP、AlP、GaP 和InP 化合物中转移的电荷分别为0.11 e、0.19 e、0.15 e、0.22 e,所以InP 和AlP 的离子性更明显,原子间相互作用力最强,热膨胀系数相对较小且随温度变化趋势更为平缓,而GaP 的热膨胀系数随着温度升高基本呈现线性增加。BP 的热膨胀系数在500 K 以下时变化趋势缓慢,但在500 K以上时会急剧增加,有着独特的变化趋势,一方面这是因为B 元素的电负性(2.00)要大于P 元素电负性(1.64),且BP是Ⅲ-Ⅴ族二元半导体材料中共价性最强的化合物,另一方面B 的原子半径小且无p 型价电子,这些特点使BP通常会展现出不同于其他磷化物的性质[44]。此外,在300 K 时,本文InP 热膨胀系数的计算值为4.89×10-6K-1,这与实验值4.6×106K-1非常接近。
3 结 论
本文通过密度泛函理论以及声子模型,系统研究了第Ⅲ族元素磷化物BP、AlP、GaP 和InP 的结构性质及其在0~1000 K 温度范围内的热膨胀系数和热力学函数。计算了四种磷化物的晶胞边长和化学键长,并与实验及其他理论计算值进行了比较,发现结果比较接近,晶胞边长大小次序为InP >AlP ≈GaP >BP,这主要是原子半径及电负性共同作用的结果。计算了四种磷化物的声子曲线,发现均无虚频,说明物质具有动态稳定性,并且因为磷原子和第Ⅲ族原子间存在质量差,可以看到声子曲线中的声学分支和光学分支间存在一定带隙。利用声子态密度计算了焓、熵、热容这些热力学性质,焓和熵会随着温度升高而单调递增,而热容则会在低温时呈现指数增长,在T>700 K 时BP、AlP、GaP 和InP 的热容均近似趋于Dulong-Petit 极限值49.9 J·(mol·K)-1。通过不同温度下的平衡体积计算了材料的热膨胀系数,由于InP和AlP中原子间相互作用力最强,热膨胀系数相对较小且随温度变化趋势更为平缓,而GaP 的热膨胀系数随着温度升高基本呈现线性增加,BP 的热膨胀系数在500 K 以下时变化趋势缓慢,但在500 K 以上时会急剧增加。这些数据的计算值有助于研究人员很好地理解第Ⅲ族磷化物在高温下的特定行为,开发其在光电材料领域的应用。
符 号 说 明
B——材料在温度为T时的体积模量,Pa
CV——材料在温度为T时的等容热容,J·(mol·K)-1
Cp——材料在温度为T时的等压热容,J·(mol·K)-1
Etot——第一性原理计算的体系在0 K 时能量,kJ·mol-1
EZP——由声子态密度计算得到的零点振动能,kJ·mol-1
F(T)——温度为T时的Helmholtz自由能,kJ·mol-1
G(T)——温度为T时的Gibbs自由能,kJ·mol-1
h——Planck常数,6.63×10-34J·s
kB——Boltzmann常数,1.38×10-23J·K-1
N——体系自由度
S(T)——材料在温度为T时的熵,J·(mol·K)-1
U(T)——材料在温度为T时的内能,kJ·mol-1
α——体积热膨胀系数,K-1
ω——声子频率,Hz
g(ω)——声子态密度

