立体几何中的动点轨迹问题

福建省南安国光中学 黄清波 362321

立体几何中的动点轨迹问题是较为新颖的一种创新命题形式，它重点体现了在解析几何与立体几何的知识交汇处设计图形.不但考查了立体几何点、线、面之间的位置关系，而且又能巧妙地考查求轨迹的基本方法，是表现最为活跃的一种创新题型.这类题型因涉及动点的轨迹问题从而使得要解决的问题处于动态变化之中，需要学生有敏捷的数学观察力和熟练的转化能力，技巧性强且难以操控，对学生知识以及思维能力要求较高.本文以福建省泉州市2020届普通中学高中毕业班质量检查理科卷第12题为例,对这类问题的解法进行剖析，希望对大家有所帮助.

题目：直四棱柱ABCD-A1B1C1D1中，底面ABCD是边长为4的正方形，AA1=23．点M是侧面BCC1B1内的动点（不含边界），AM⊥MC，则A1M与平面BCC1B1所成角的正切值的取值范围为．

命题意图：本题涉及到动点的轨迹问题，表面上是求线面角，实际是转化为考查空间图形的截面轨迹问题，考查了化归与转化的思想，考查直观想象、逻辑推理和数学运算核心素养，体现基础性与创新性，有一定难度,本次质检得分率极低.

策略一：降维法

思路分析：根据题意，画出图形，对于平面BCC1B1来说，AM是斜线，点M是斜足，AB是垂线，点B是垂足，所以BM是射影，因为AM⊥MC,得到MC⊥BM，所以点M在平面BCC1B1内的轨迹是以BC为直径的半圆（不包含B,C点）.因为A1B1⊥平面BCC1B1,所以∠A1MB1为A1M与平面BCC1B1所成角.结合B1M的取值范围，即可得正切值的取值范围.

解法1:如图1，已知四棱柱ABCDA1B1C1D1是正四棱柱，所以AB⊥平面BCC1B1.又MC⊂平面BCC1B1,所以AB⊥MC.因为AM⊥MC，AB⋂AM=M,所以MC⊥平面ABM.又BM⊂平面ABM，所以MC⊥BM.因为点M是动点，点B,C是定点，所以在平面BCC1B1内点M的轨迹是以BC为直径的半圆（不包含B,C点）.因为A1B1⊥平面BCC1B1，所以∠A1MB1为A1M与平面BCC1B1所成角.在RT△A1MB1中，.取BC的中点N，由已知得又A1B1=4，所以tan∠A1MB1的取值范围为

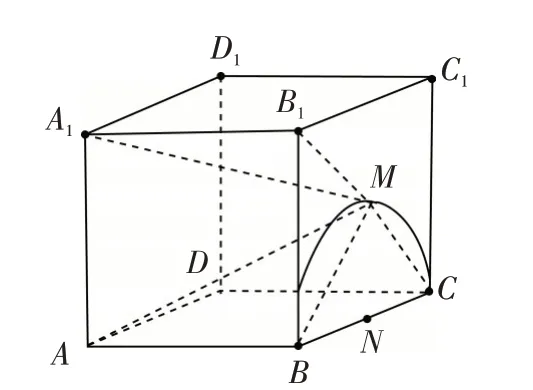
图1

归纳：降维法，即空间问题平面化法，利用立体几何的相关知识把空间的几何量关系、位置关系等转化到同一平面内，空间问题平面化，然后结合解析几何中有关轨迹定义（如圆、椭圆、双曲线、抛物线、线段垂直平分线、角平分线等），求出对应的轨迹.常用的方法有：平移法、射影法、展开法、辅助面法等.

变式：如图2，在正方体ABCD-A1B1C1D1中，点P为BCC1B1面内一动点，若点P到直线BC与直线C1D1的距离相等，则动点P的轨迹所在的曲线是（ ）.

A．直线 B．圆

图2

C．双曲线 D．抛物线

解：因为点P到C1D1的距离即为点P到C1的距离，所以在平面BCC1B1内，点P到定点C1的距离与点P到定直线BC的距离相等.由圆锥曲线的定义可知，动点P的轨迹为抛物线，故选D.

策略二：交轨法

思路分析：根据题意，画出图形，在空间中，AM⊥MC，取AC的中点O,则点M的轨迹是以AC为直径的球面O.点M是侧面BCC1B1内的动点，所以点M是球面O与平面BCC1B1的公共点.则点M在平面BCC1B1内的轨迹是以BC为直径的半圆（不包含B,C点）.以下同解法1.

解法2：如图3，在空间中，AM⊥MC，点M是动点，点A,C是定点，取AC的中点O,所以点M的轨迹是以AC为直径的球面O.

图 3

又点M是侧面BCC1B1内的动点，所以点M是球面O与平面BCC1B1的公共点.取BC的中点N，则ON⊥平面BCC1B1,OB=OC.所以在平面BCC1B1内点M的轨迹是以BC为直径的半圆（不包含B,C点）.

后续同解法1.

归纳：在平面几何、解析几何中已有“交轨法”的运用，若对此有一定的知识迁移能力，则在空间图形轨迹问题中也可涉及这种重要的思考方法——交轨法，即从集合的“交”来确定兼备有关集合特性的元素.解题基本思路是：先找出符合各条件对应的点的轨迹，然后求出符合各条件对应点的公共部分.即化“动”为“静”，化“整”为“零”，各个击破.

变式：在正方体ABCD-A1B1C1D1中，点P在侧面BCC1B1及其边界上运动，总有AP⊥BD1，则动点P的轨迹为.

解：如图4，连接AC,AB1,B1C，在正方体ABCD-A1B1C1D1中，易证得BD1⊥平面ACB1，所以点P在平面ACB1上.又点P在侧面BCC1B1及其边界上运动，所以点P的轨迹为平面ACB1与平面BCC1B1的交线段CB1.

图4

策略三：空间向量法

思路分析：依题意，四棱柱ABCDA1B1C1D1是正四棱柱，以D为坐标原点，以DA方向为x轴的正方向，建立空间直角坐标系，由已知，设M(a,4,b)(0＜a＜4,0＜b＜23)，因为AM⊥MC，可得点M的轨迹方程：(a-2)2+b2=4，即点M的轨迹是以BC为直径的半圆（不包含B,C点）.以下同解法一，也可结合圆的参数方程继续求解.

解法3：依题意，四棱柱ABCD-A1B1C1D1是正四棱柱，以D为坐标原点，以DA方向为x轴的正方向，建立空间直角坐标系，则A(4,0,0),C(0,4,0),设M(a,4,b)(0＜a＜4,0＜b由AM⊥MC，有，得(a-2)2+b2=4.即点M的轨迹方程：(a-2)2+b2=4.因为A1B1⊥平面BCC1B1，所以∠A1MB1为A1M与平面BCC1B1所成角.在RT△A1MB1中，由B1(4,4,23)，M(a,4,b),得B1，设a=2cosθ+2，b=2sinθ,其中0＜θ＜π.得且，所以2≤B1M＜27.又A1B1=4，所以tan∠A1MB1的取值范围为

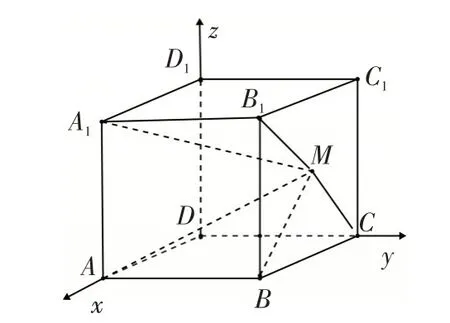
图5

归纳：立体几何中的动点问题，有些时候如果按立体几何的传统方法几乎无法入手，空间向量巧妙地解决了这一难题，将数与形完美地结合起来，降低了立几的思维难度，解题有一定的规律性，便于学生掌握.其步骤：①建系；②找点的坐标；③写出向量坐标；④结合公式进行论证、计算；⑤下结论.不规则的坐标系的建立较为灵活，但还是有“法”可依，平时教学过程中，应加强建不规则坐标系的练习，帮助学生消除心理障碍.

变式：如图6所示，正方体ABCD-A1B1C1D1中，点M是底面正方形ABCD内的一个动点，若直线C1D,C1M所成的角等于30o，则以下说法正确的是（ ）.

图6

图7

以上是几种方法各有所长，适合求解立体几何中的动点轨迹问题.一般来说，坐标法比较容易操作，但有时计算繁杂，对于那些不规则坐标系的习题尤其如此；降维法、交轨法技巧性强，但也是有规律可循，平时学习备考中坚持多法并举，择优而取，以增强解题的技术水平和效益.