平余式运算规则
——从平面数到孙子共数的求解
张国平
(福建省南平市福州大学 353416)
在孙子算经中:“今有物不知共数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何”.
那么,由题我们首先转换成数学思考则是:
假设其共数为y,则y=3x1+2;y=5x2+3;y=7x3+2;由于数之是次数,故x1,x2,x3为整数.
现将上述思考转换成‘平余式’表达式则为[3,2];[5,3];[7,2].则我们要寻求的就是关于平余式的运算规则,但在此,我只给出解题过程,而把平余式的运算规则附在后面.
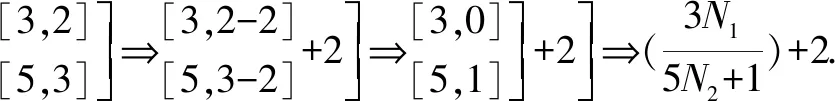
寻找3N1与5N2+1的最小公倍数⟹6+2=8.
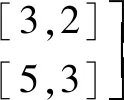
再由[15,8]与[7,2]运用平余式规则进行如下运算:
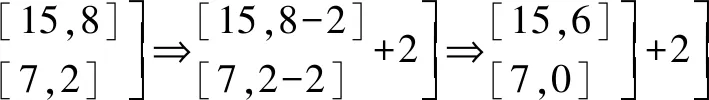
寻找15N1+6与7N2的最小公倍数⟹21+2=23.
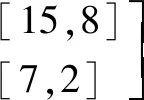
即孙子共数 [3,2];[5,3];[7,2] 运用平余式规则求解的共数为[105,23]或是y=105x+23的整数值,所以,它的解不是一个数而是一类数.
附:平余式运算规则原始思考如下:
假设平余式[a1,k1];[a2,k2](其中k1,k2,a1,a2∈Z且a1≠0,a2≠0,a1,a2不可约(互质)).
①若a1=a2,k1=k2(即k1=k2±a1).
则条件组合为复式,其本身就是类解.若a1=a2,k1≠k2(即k1≠k2±a1)则条件组无共数或共数为空.
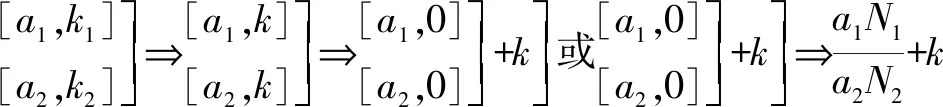
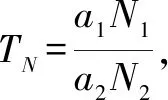
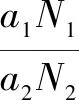
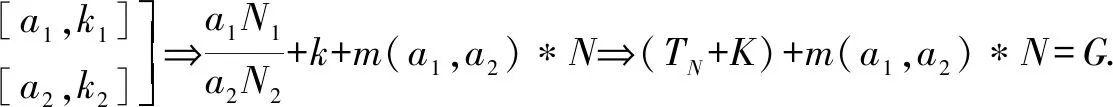
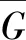

所以:G=(TN+K1)+m(a1,a2)*N(跳跃数).

故而,当平余式(条件式)运算规则确立后,素数的递推式也就由此呈现,但里面并不是单一和纯粹的.
平余式运算法则:[a,b]相与y=ax+b的整数值
[a,b]= [a,b±a];
[a,b]±m= [a,b±a] ±m=[a,b±a±m]= [a,b±m]
[a,b]*m= [a,b*m]; [a,b]n= [a,bn];
[a,b]±[a,c]= [a,b]±c= [a,b±c];

平余式运算的逆运算——共数的逆向求解
设平余式[a,b],[c,d],[e,f].
假若[a,b][c,d]=[e,f](a与c互质).
现已知:[c,d],[e,f] (a,c互质),求[a,b].
解由平余式公式知e=a*c⟹a=e÷c,a*N=f-b(0≤b

