数形表征 猜验递进

王志艳 马天红

摘  要：探索性学习过程中学生经历观察、比较、猜想、验证等一系列活动，其中猜想验证活动能有效促进学生学习能力、知识系统、思维的发展。教师提供的学习材料以什么形式出现？怎样突出材料的特征才能有效促进学生提出问题、合理猜想并积极验证呢？经过两次不同的教学设计，笔者认为数形结合表征，逐步实现猜验递进更有助于学生自主探索学习。

关键词：数形;猜验;树叶中的比;教学设计

■【教学内容】

苏教版六年级上册第66-67页综合与实践“树叶中的比”。

【教学片段一】观察比较，提出问题。

第一次教学设计：

出示教材主题图，观察这些树叶的形状，你有什么想法？

预设：形状和大小各不相同。同一种树叶有大有小，形状都差不多;有些不同种类的树叶形状也很像。

师：可以用什么描述树叶形状呢？讨论。

第二次教学设计：

1. 认识树叶，观察比较。

课件出示树叶形状，除了呈现教材中的主题图，还增加了树叶拓印画和剪影画。

师：辨认时你是怎么想的？

2. 怎样表示一片树叶的形状？

预设：长或宽，长与宽的比值。

师：用哪个数表示更合适？组织讨论，鼓励举例子说明。

3. 介绍柳叶长、宽以及测量的方法。

师：如果计算出它们长与宽的比值，你能想到什么问题？

预设：树叶形状与长宽的比值之间有什么联系？

评析：问题是数学的核心，是激发学习兴趣的重要因素，而问题来自对现象的观察与思考。第一次的设计直接呈现教材中各种各样的树叶：色彩丰富，形状各异，有单生叶也有复生叶，但对于提出“用什么来表示树叶的形状”这一问题有干扰。学生根据已有知识经验，自然想到用长、宽来表示树叶形状。老师只好尴尬地引导学生：用长、宽的比值来表征更简便。第二次设计中，教师呈现树叶实物图、拓画图片以及剪影图片，在观察比较树叶的大小形状时凸显了形状的相似与不同，由此提出问题，能有效地激发学生的探究欲望。在讨论的过程中，鼓励学生用实例表达自己的观点，用类比的方法阐述长、宽的比值是最合理的方式。数与形状对照是研究树叶形状，激发数学思考的重要方法。

【教学片段二】观察比较，引导猜想。

第一次教学设计：

师：这些树叶长与宽的比值可能会怎样？

预设：同一种树叶长与宽的比值相近，不同种类的可能接近。

第二次教学设计：

1. 形状与长和宽的比值之间有什么联系？

预设：形状特别的可以不研究。有的树叶相似，长与宽的比值有没有可能相同或相近呢？

2. 数形结合启发思考。

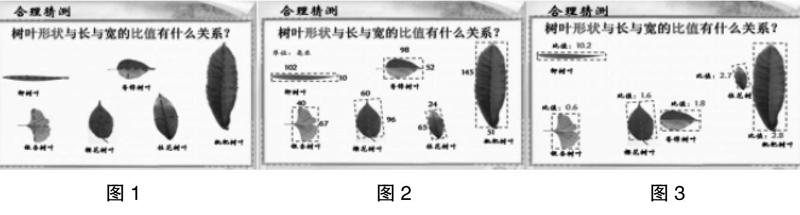
我们描出长与宽，大家算一算比值。（呈现图1）

师：算出比值后，你能把这些树叶分一分吗？（呈现图2）

出示分的结果（呈现图3）。

师：这时，你想到什么？

根据回答依次出示——

同一种树叶：①长与宽的比值相近？

不同种类：②形状不同，比值不同？

③形状相似，比值相近？

④比值越大，形状越（    ）。

评析：教学中教师应努力打开文字、图形与符号之间的通道，让学生获得这些不同信息之间的内在联系，让形象思维和抽象思维和谐共舞，促使有思维深度的数学猜想成为可能。第一次的设计在学生还没有充分理解长宽比值与树叶形状之间联系的时候，教师紧接着引导学生对比值进行猜想，显得非常仓促。经过分析得出，学生思考形状与长宽比值有什么联系，需要强烈的信息刺激，使直觉易于产生作用，产生跟树叶形状与长宽比值相关的直接想法。所以第二次的设计，教师将研究的对象以数形结合的形式出现时，学生的已有知识和生活经验更容易被充分调动，尤其是借助长方形的长与宽的构图以及长与宽的具体数据来想、来猜。学生自然地经历了从经验中想、从知识中想、从数据中猜的过程。当然，从数据中来的猜想最有价值，也最可靠。

【教学片段三】表征数据，设法验证。

第一次教学设计：

1. 研究同一种树叶。

（1）算出柳树叶长与宽的比值。

师：观察大家计算的比值，你有什么想法？

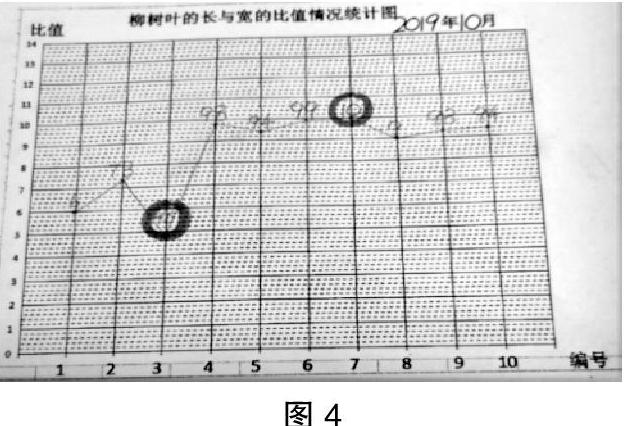
活动：把10片柳树叶长与宽的比值制成折线统计图，用红笔圈出最大值，用蓝笔圈出最小值（如图4）。

思考：用哪个数来描述柳树叶长与宽的比值更合适？（平均数）

师：算一算平均数。汇报平均值最大、最小分别是多少。

（2）比较平均数。

师：老师在电脑上用统计图表示大家的平均值在哪个范围。（只出示最大、最小值）

师：观察从每一片柳叶到10片平均值的数据变化，你想说什么？（范围变小，更集中，更有代表性，片数再多一点会怎么样呢）

算出一组6个人的平均数。在统计图中呈现最大值和最小值并比较。

算出全班同学的平均数，呈现在统计图中。

问：通过计算、比较和分析，你有什么收获？

2. 研究不同的树叶。（略）

评析：第一次设计利用统计图表示两个极值，经历从10片到60片，再到几百片树叶的长宽比值平均数的变化，使学生感受统计的数量越多，平均数的最大值和最小值数值越接近。这有助于发展学生的数据观念，以寻找更合适的表示树叶形状的比值。一般为了促进学生研究，形状与数值的内在联系应该直观外显，可这里的数据与树叶形状是分割的，数据与树叶形状之间的内在联系学生无法体会，导致思维活动低效，不利于发现规律，形成与猜想相應的结论。开展数学实践活动，要使学生从多角度体验、了解数学（如比值）的价值。课堂上教师虽适当引导启发，有利于活动走向深入，学生的确也经历了用动手实践、自主探索、合作交流等方式去探索相关规律，但偏重于统计数据的比较，无论从观察、比较还是分析的角度来看，都无法将学生的思维向数形关系的深处引导。

第二次教学设计：

1. 讨论验证方法。

师：怎样验证呢？

预设：测量、计算、比较。

2. 小组合作，验证猜想。（选择一条猜想进行验证）

3. 交流分享。

将研究的树叶贴出，分享：本组验证哪条猜想？发现了什么？

形成过程性板书，如图5。

提醒学生将树叶实物图按照一定的顺序排列。用一个数轴（纵轴）呈现所有研究的树叶实物图和长宽比值。

评析：苏霍姆林斯基说，“在人的心灵深处，都有一种根深蒂固的需要，这就是希望自己是一个发现者、探索者”，验证猜想的活动给予学生充分自由的学习空间。小组合作既有利于学生共享树叶资源，进行不同猜想内容的验证，又能在验证同一个猜想时获得更多数据，更能体现研究对象的特点。验证方式可以有：①举例子，举例子的操作核心是找到反例，如果没有反例，那就猜对了，如果有反例就可以否定;②说理，说理可以用不同的形式进行表征，也可以进行证明等。在与学生交流分享同步进行的板书中，数据呈现也可以为学生的验证提供更直观的感悟：用一个数轴（纵轴）呈现所有研究对象及其分享的数据（长宽比值），通过观察发现有的数据接近，同时将树叶图片也呈现在相应的位置，数形对照，验证猜想。

总体来说，第一次教学设计，学生不能主动理解用“长、宽比值”表示树叶形状;学生对“树叶形状与长宽比值的大小之间有什么规律”的猜想比较被动。整个学习活动中，教师引导过多，学生比较盲从。修改的重点是：更换学习素材和素材呈现方式，以启发学生提出有针对性的问题;突出树叶与其长、宽、长宽比值的对照，采用数形结合的方式帮助学生理解、分析和猜想;舍弃统计图的呈现方式，改用数轴的方式出示树叶形状与长、宽比值，让规律看得见、说得出、想得清。

数学猜想与验证需要每一个学生都亲历“提出疑问、大胆猜想、合理验证、完善结论”的实践过程，更需要教师引导学生对研究对象进行数形结合的观察、思考、比较、计算等活动。学生建立在对物质世界直接经验之上的真正的学习，使数学活动成为有趣的、深受学生喜爱的、能被学生理解的学科性活动。“树叶中的比”这一“综合与实践”活动仅凭一片树叶长与宽的比值，难以得出任何结论，但是当我们把多片的同种树叶进行比较、把不同种类而形状相似的树叶放在一起比较、把不同种类且形状不同的树叶放在一起比较时，数据就会有规律，与数据相应的形状便随之呈现出一些明显的有规律的现象。在材料数据从长、宽到长宽比值，再到結合数形比较和分类的过程中，猜想活动不断推进。几次进行猜想，经历验证、归纳和发现其中隐含的数学规律，是学生重要的学习手段。