在合理猜想设法验证中发展学生思维

刘芸

摘  要：新课程标准倡导自主发现式学习，猜想验证是自主发现学习模式中的一个重要组成部分，在培养学生自主学习能力和发展学生思维等方面具有重要作用。文章重点阐述了猜想验证在小学数学课堂中的运用，通过合理猜想设法验证活动发展学生思维，提升小学生的数学学习水平。

关键词：合理猜想;设法验证

■【案例背景】

新课程标准指出：“归纳概括得到猜想和规律，并加以验证，是创新的重要方法。”由此可见，“提出问题―合理猜想―设法验证―得出结论”既是一种有效的教学模式，更是一种学生需要掌握的重要学习方法。让学生在问题情境中进行大胆假设，有了合理的猜想后，再设法用各种验证的方法验证猜想是否正确，通过这样的一个探究过程，得出最后的结论。作为教师，我们应该在教学中有意识地培养学生猜想和验证的能力，通过我们不断地研究和尝试，探索形成学生猜想和验证能力的模式，从小培养学生合理猜想与设法验证的意识和能力，引领学生投入高效的探究活动中，在教学实践中逐步发展学生的思维，提升学生的数学素养。

■【案例描述】

在教学苏教版五年级上册《钉子板上的多边形》时，笔者采用的是合理猜想设法验证式的教学模式，引导学生在自主探索中加深对知识的理解，在潜移默化中不断发展自己的思维。

一、提出问题，引发思考

本节课一开始，笔者给学生出示一块钉子板，让学生猜一猜今天可能要研究什么问题，接着提出问题：“多边形的面积可能与什么有关？”

学生大胆猜想：多边形的面积可能和围成的图形里面的钉子数有关，还可能和围成的图形边上的钉子数有关。

二、开展研究，揭示规律

1. 初步探究，发现规律。

（1）出示图片（如圖1），填写表格。

师：请你算出这4个图形的面积和边上的钉子数并填写表格。

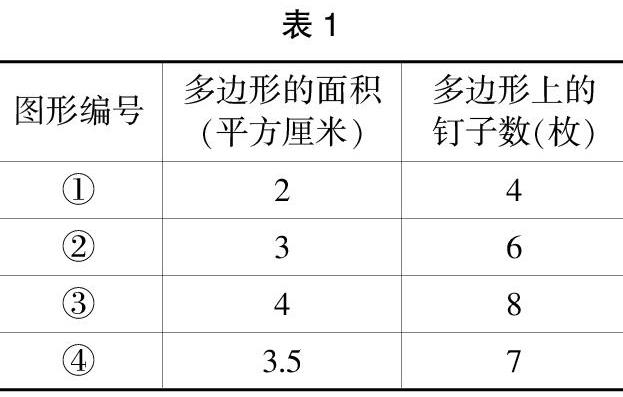
（2）观察表格（见表1），合理猜想。

生：我发现多边形边上的钉子数是多边形面积的两倍。

师：如果用S表示多边形的面积，n表示边上钉子数，你能用字母简洁地表示出它们之间的关系吗？（S=n÷2）

（3）设法验证，质疑反思。

师：分别计算下面三个图形的面积和边上钉子数，验证刚刚的猜想是否正确。（图2）

（4）观察反思，得出结论。

师：现在把两组图形放在一起，请你观察比较，想一想为什么刚刚没有验证成功。（图3）

生：上面一排的多边形里面钉子数是1，下面一排的多边形里面钉子数是2，我发现只有当多边形里面只有一颗钉子时，S=n÷2才成立。

师：从上面几个多边形中我们得到了这样的结论，那是不是只要多边形里面有一颗钉子，就都符合S=n÷2？请你任意画一个里面钉子数是1的多边形，验证这个猜想对不对。

集中交流学生验证的结果并提问：有没有谁的验证是不符合S=n÷2的？

通过再次验证且没有找到反例，最终得出结论：当多边形里面只有一颗钉子时，S=n÷2。

师：请你猜想，当多边形里面有2颗钉子时，多边形的面积和边上钉子数有怎样的关系？

学生猜想：S=n÷2+1。

师：请你设计一个里面有2颗钉子的多边形，验证你的猜想是否正确。

学生集中汇报验证的成果，注意寻找有没有验证不成功的例子，在交流反馈中确认设法验证后的结论。

2. 深入探究，完善规律。

师：请你继续猜想，当多边形里面有3颗钉子时，多边形的面积和边上钉子数又会有怎样的关系？若多边形里面的钉子数是4呢？是5呢？是6呢？……

出示活动要求： ①猜一猜：当里面钉子数是（   ）时，S=（         ）

②验一验：画一个多边形验证你的猜想。

学生依次说出自己的猜想，并验证猜想是否正确。

3. 拓展延伸，揭示规律。

（1）总结规律，得出结论。

师：通过刚才的验证，我们发现这些猜想都是正确的。当多边形里面钉子数就是a的时候，S=n÷2+a-1。通过今天的合理猜想和设法验证，我们最终得出了这个结论。

（2）交流提升，应用拓展。

师：孩子们，你们知道吗，你们今天做的事情，数学家们也在做。1899年，有一个伟大的数学家用了一种数学归纳法，证明这些结论都是正确的。播放音频，介绍皮克定理的相关知识。

三、回顾反思，交流提升

师：本节课的最后请你说一说，我们是怎样探究和发现规律的？你有哪些收获？你会用今天学习的猜想验证的方法探究事物的规律吗？

师：回顾今天这节课，我们是先提出问题，然后进行合理猜想，设法验证，得出结论，通过猜想验证式的探究模式发现了数学家们也在研究的皮克定理。

■【案例反思】

本节课笔者创新教学，用猜想验证式的学习模式贯穿始终，引导学生在多次的猜想和验证中发现了皮克定理。回顾本节课，笔者始终在思考：如何才能让学生的猜想合理？如何才能让学生的验证有效？如何才能开展高效的“猜想验证”活动？要想解决这些问题，需要在实际教学中注意以下几个方面的内容。

一、重视情境的有效性，激发学生的猜想欲望

本节课一开始，笔者给学生出示一块钉子板，让学生猜一猜今天可能要研究什么问题，接着提出问题：“多边形的面积可能与什么有关？”学生大胆的猜想开启了本节课的教学，通过从生活实例中抽象出数学问题，开门见山式的导入，激发了学生的好奇心和求知欲。要想激发学生合理猜想的欲望，一是要求所选的问题都对学生的猜想具有一定的启发性和暗示性，这样在猜想时，学生就不会做出漫无目的的猜想;二是要给学生充足的时间观察和思考，表达自己的发现，并引导学生在发现的基础上提出自己的猜想。

如果教师想要学生做出有一定的科学依据和针对性的猜想，那么就要重视问题情境的有效性，并且鼓励学生先仔细观察再提出猜想，这样的“猜想”一定是有根有据的。在本节课中，学生通过观察四个图形，猜想：S=n÷2，并继续让学生猜想是不是所有图形都有这个规律？怎么来验证这个猜想呢？首先出示三个图形让学生验证猜想是否正确，当学生产生认知冲突时，教师继续引导学生在观察比较中完善自己的猜想，接着通过举例继续验证猜想的正确性。

选择与运用恰当的情境，能够引导学生自主参与到探索的活动中去，这对于学生兴趣的激发、经验的唤醒、数学的理解、思维的深刻等方面都起到了至关重要的作用，真正使课堂教学潜移默化、润物无声！

二、重视验证的过程性，提升学生的验证能力

如何使验证的过程真实有效，是教学《钉子板上的多边形》时一个值得深思的问题。

在本节课中，当學生初步感知得出S=n÷2后，笔者又出示了三个图形让学生验证这个猜想是否正确，当学生产生认知冲突时，引导学生仔细观察图形，深入思考为什么没有验证成功，从而得出只有当多边形里面仅有一颗钉子时，S=n÷2才成立。紧接着，笔者让学生猜想当多边形里面有2颗钉子时，多边形的面积和边上钉子数又有怎样的关系。学生大胆猜想后，再自行设计一个里面有2颗钉子的多边形，验证猜想是否正确。接着，笔者继续让学生猜想当多边形里面钉子数是3、4、5……又会有怎样的规律，并设法一一进行验证。通过这样反复的猜想和严谨的验证，最终得出规律：当多边形里面钉子数是a的时候，S=n÷2+a-1。

验证过程如果仅仅停留于表面，依样画葫芦，那么仅仅只是一种“伪验证”或“形式验证”，起不到真正的作用。只有真正为得出结论服务的，与结论紧密结合的严谨的过程才是真正的验证过程。

三、重视结论的反思性，激发学生的质疑能力

结论的验证过程必须是科学的、严谨的，并且是具有一定挑战性的。爱因斯坦曾言：“探索真理比占有真理更为可贵。”仅仅满足于得到一个结论，那么依旧是老师“给”的，而不是自己“得”的，学生的学习能力便得不到发展。在本节课中，当学生发现S=n÷2后，笔者通过出示三个图形让学生验证这个猜想是否正确，成功激起了学生的认知冲突，引导学生思考：为什么没有验证成功？学生在反思质疑中得出：只有当多边形里面有一颗钉子时，S=n÷2才成立。在学生得出结论的过程中，笔者引导学生反思整个猜想验证的过程，说一说“我们是怎样探究和发现规律的？你会用今天学习的猜想验证方法进行验证吗？”通过这一环节，让学生感受验证过程对得出结论的支撑作用，激发学生思考问题和解决问题时的质疑能力。

在新课程理念的影响下，数学课堂正在发生着悄然的质的变化，教学内容应具备数学思维性与数学研究的理性精神。学生学习的过程应该经历这样几个步骤：提出问题―合理猜想―设法验证―得出结论―回顾反思。作为教师，一定要践行这样的教学模式，让学生在“猜想”“验证”“归纳”到最后得出结论的过程中发展自己的思维，提升自我的数学素养，实现数学水平的大飞跃。