基于余弦自卷积窗的高精度介质损耗角测量算法

张超，邱衍江，王维庆，王海云

(1．广东电网有限责任公司广州供电局，广东 广州 510620；2．可再生能源发电与并网技术教育部工程研究中心(新疆大学 电气工程学院)，新疆 乌鲁木齐 830047；3．广东电网有限责任公司江门供电局，广东 江门 529030)

在电力系统中，系统的安全稳定运行与绝缘条件有关。当高压设备发生绝缘事故时，不仅会损坏设备，还会造成重大经济损失[1]。电容型器件绝缘状况可以通过介质损耗角(dielectric loss angle，DLA)这个重要指标进行衡量，它是目前预防性试验的主要内容。快速准确的DLA监测和计算可为电气设备故障诊断提供可靠依据，为电力系统安全经济运行提供重要保障。

目前主要通过硬件法和数字测量法对DLA进行测量，前者易受噪声等外部条件干扰，导致不可忽略的测量误差。后者主要包括高阶正弦拟合法、过零时差法、滤波法和快速傅里叶变换(fast Fourier transform，FFT)及其改进算法。其中，FFT因为计算量小、易实现且直流分量和谐波分量影响小，应用最为广泛[2-4]；然而，使用FFT方法测量设备的DLA很容易发生频谱泄漏和栅栏效应[5-6]。为了减少异步采样下的检测误差，一般采用截断窗对信号进行加权，以减少谱泄漏对测量精度带来的影响，最常用的截断窗函数包括包括Hamming窗[7]、Hanning窗[8]、Nuttall窗以及各种余弦组合窗[9]。对于栅栏效应，通常使用双谱线[10]、三谱线和四谱线插值校正算法[11-12]。

电容器件的DLA是一个微小的值，通常为0.001～0.02 rad；因此，测量算法必须在满足检测效率的前提下具有较高的分析精度。目前常用单窗函数旁瓣性能较差，虽运用简便但无法达到高精度的工程要求；因此，通过卷积运算并以8项余弦窗为母窗构造余弦自卷积窗(cosine self-convolution window，CSCW)函数，同时考虑到主瓣性能和旁瓣性能指标，选用2阶CSCW函数对信号进行截断。多谱线插值算法检测精度略高于双谱线插值校正算法，但分析时延与计算量也随之增加，无法实现高效、高精度检测功能；因此，提出一种基于2阶CSCW函数的双谱线插值FFT高精度DLA测量方法，利用曲线拟合函数推导出实用的校正公式。通过仿真及对比分析，对所提DLA测量算法的检测精度和实用性进行验证。

1 基于CSCW的DLA测量原理

交流电压下的电容型器件等效模型如图1所示。其中：R为介质的等效电阻；C为介质的等效电容；IC为流过电容元件电流；IR为流过电阻元件电流；I(t)为流过电容型器件干路电流；U(t)为电容型器件端口电压；I与U为I(t)和U(t)的模值；θ为通过电介质的电流与施加的电压之间所夹相位角；δ为θ的余角，即DLA[13-14]。在实际应用中，δ的正切值tanδ(介质损耗因数)常用于表征介质损耗水平的特征值，对tanδ的测量可转换为对δ的测量。在图1中的电容性设备中加入电压u(t)与电流i(t)：

u(t)=Umsin(ωt+φu)，

(1)

i(t)=Imsin(ωt+φi).

(2)

式中：φu、φi为电压、电流的基波相位；Um、Im为所加电压、电流的峰值；ω为角频率；t为时间。

图1 电容型设备绝缘等效电路与相量图Fig.1 Equivalent circuit and phasor diagram of capacitive equipment insulation

根据图1所示的电容器件等效模型，δ的测量公式由式(3)表示，即将δ的测量变换为求解电压与电流基波相位的差值：

(3)

如上所述，DLA是一个微小的值，对算法的测量精度要求严苛。当电网中存在谐波或发生频率波动时，由于频谱泄漏现象及栅栏效应，会大幅度降低传统FFT对于初相位参数的提取精度。为了提高DLA的测量精度，本文提出一种基于CSCW函数的双谱线插值DLA测量算法。

余弦截断窗是一种具有出色旁瓣性能的组合函数，相比于其他窗函数，可以很好地抑制远程与近程频谱泄漏，其时域表达式为[15-16]

(4)

式中：n=0,1,2,…,N-1，N为窗函数数据长度；M为函数的项数；bm为窗函数中第m项的参数系数，通过改变bm的取值，可以得到不同的余弦组合截断窗。

余弦窗的离散傅里叶变换(discrete Fourier transform，DFT)为

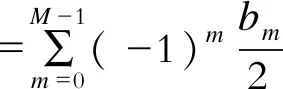
(5)

(6)

式中：WN(ω)为余弦窗函数的频域表达式；WR(ω)为矩形窗函数的谱函数。通常，数据长度N远大于1，则余弦截断窗的DFT为

(7)

CSCW可定义为几个余弦窗函数的自卷积运算结果。p阶CSCW序列由p个长度相同的余弦窗序列作p-1次离散卷积，并首尾补零所得，即

wp(n)=w(n)*w(n)*…*w(n).

(8)

式中wp(n)表示p阶CSCW离散序列。

时域中的函数作卷积运算后再进行FFT运算，相当于分别进行FFT运算后得到的结果再进行乘积运算。简而述之，时域卷积对应着频域作乘积，则p阶余弦自卷积窗的离散频率响应

Wp(ω)=[W(ω)]p.

(9)

基于CSCW函数的插值FFT DLA测量算法主要包括加截断窗、DFT、插值校正和DLA计算等步骤，算法流程如图2所示。

图2 算法流程Fig.2 Algorithm flow chart

待分析数据加CSCW窗并通过插值FFT运算，可有效降低谱泄漏和栅栏现象对参数检测精度的影响，提高电压、电流的基波相位参数的提取精度，实现高精度DLA测量。

2 基于CSCW的DLA测量算法

2.1 CSCW的频域特性

根据式(7)绘制如图3所示的典型余弦窗函数幅频响应曲线。在0.5 Hz时，8项余弦截断窗的旁瓣峰值电平为89.69 dB，旁瓣衰减率最大，相比于其他窗函数，其具有更加优良的旁瓣特性；因此，本文以8项余弦窗为卷积窗函数的原始母窗[17-18]。

基于8项余弦窗的1～4阶自卷积窗函数的归一化对数谱(N=128)如图4所示。可以看出，随着卷积阶数p的增加，CSCW函数的旁瓣性能迅速提高，但主瓣宽度也随之降低，且3阶与4阶卷积

图3 典型余弦窗的幅频响应曲线Fig.3 Frequency response of typical cosine windows

窗函数频谱已经发生失真现象。考虑到这2个因素，本文使用2阶CSCW函数对信号进行加权，以有效地抑制谱泄漏对检测精度的影响。

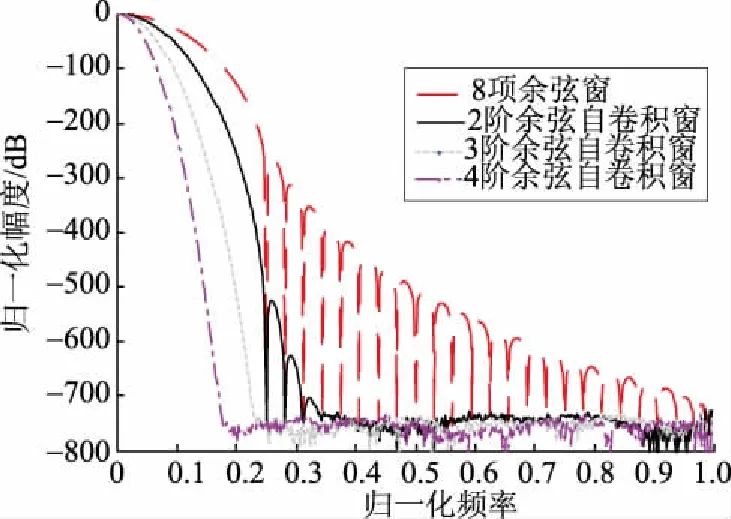
图4 基于8项余弦窗的自卷积窗函数幅频响应曲线Fig.4 Amplitude-frequency response curves of self-convolution window functions based on 8-term cosine window

2.2 基于2阶CSCW双谱线插值DLA测量算法

栅栏效应在异步采样时发生，且待检测的信号频率不是采样频率fs的整数倍；因此第k个谐波频率分析结果与之相对应频点的真实频率值不一致，需要进行插值校正。由于选用8项余弦窗为母窗，且以2阶卷积窗为截断窗，检测精度在一定程度上已得到极大改善。为了减少计算量并改善延迟特性，本文选择双谱线插值校正算法。设第h次谐波准确频点kh附近的2根谱线分别为kh-1和kh+1，谱线的幅值分别为y1与y2[19]，设共含H次谐波信号采样后离散序列

(10)

式中Ah、fh、φh分别为第h次谐波的幅值、频率、相位。

首先采用2阶CSCW函数wp(n)对信号进行截断，则信号的频谱函数

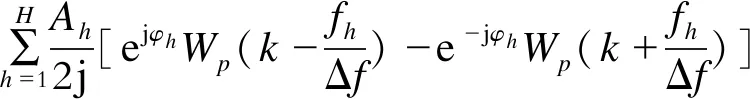
胜利油田坚持线上线下融合，用互联网思维全方位打造“身边的共青团”，先后运用“1+100”平台与883名青年建起了规模化的朋友圈，运用“胜利油田青年之声”系统实现了团的工作网上发布、青年的声音网上听取、青年的意见网上搜集，累计提问1378个，浏览48万次。北化院团委推出“春雨行动”，通过润物细无声的关心关爱和思想引领，帮助青年在成长道路上有新的发展。

(11)

式中：k=0,1,2,…,N-1；Δf为频率间隔。忽略负频点处谱峰的旁瓣影响，式(11)可简化为

(12)

为方便插值公式推导，忽略其他次谐波影响并单独分析第h次谐波信号参数，则式(12)变为

(13)

记α=kh-kh-1-0.5，由于0≤kh-kh-1≤1，则α取值范围是[-0.5, 0.5]。另记

(14)

将式(7)和式(9)代入式(14)，β可以被认为是α的函数，即β=f(α)。由于系数bm为实系数，频率响应是偶对称的，因此f(·)和f-1(·)均为奇数函数。在[-0.5, 0.5]区间取1组数据，代入可得1组β，利用MATLAB中polyfit(β,α, 7)函数对式(14)进行反拟合，表达式为

α≈0.300 5971β7+0.468 657 4β5+

0.937 500 4β3+3.750 000β.

(15)

求得频偏后，可以通过式(16)对第h次谐波频率参数进行校正：

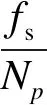
(16)

式中Np为p阶余弦窗函数长度。

第h次谐波的幅值与相位计算式为：

(17)

φh=arg(X(kh±1))-arg(Wp(-α±0.5)).

(18)

3 算法精度验证

3.1 稳态信号检测精确度对比分析

为了进行对比分析，分别采用加4项3阶Nuttall截断窗、Hanning截断窗三谱线插值校正算法，加8项余弦截断窗的四谱线插值校正算，加2阶Hanning自卷积截断窗(Hanning self-convolution window，HSCW)的双谱线插值校正算法作为对照组，与本文算法共同对谐波信号进行参数估计。幅值、频率及相位参数的检测结果如图5、6、7所示。

图5 幅值相对误差比较Fig.5 Comparison of relative errors of amplitudes

图6 频率相对误差比较Fig.6 Comparison of relative errors of frequencies

从图5可以看出，本文算法具有最高的基波和谐波幅度检测精度，相对误差小于10-14%。与其他分析算法相比，检测精度有数量级的提高。例如采用4项3阶Nuttall截断窗时，2次谐波信号的幅值检测相对误差为10-5%，使用本文算法进行幅度检测的相对误差为10-14%，改善效果非常明显。除此之外，虽然基于Hanning窗的DLA检测算法针对6～14次谐波幅值参数的分析结果整体波动性最小，但参数的估计效果远不如本文算法理想。

由图6与图7可见：采用本文算法对仿真信号的频率及相位检测相对误差分别小于10-15%和10-12%；针对频率参数检测结果，除对照组中个别算法检测误差较大之外，其余算法均能够实现高精度的频率参数检测功能；针对相位参数检测结果，采用其他对照组算法的相位检测相对误差均大于10-9%。例如250 Hz谐波信号的相位检测结果，采用基于2阶HSCW的双谱线插值校正算法的相对误差为10-6%，本文算法相对误差为10-13%，算法精度有了数量级的提高。因DLA测量精度主要依赖信号初相位参数的提取精度，本文算法的初相位参数检测相对误差为10-14%，可以高精度实现目标要求。

综上所述，本文算法显著提高了谐波信号参数检测的准确性，能够准确检测基波及谐波的频率特征值，实现较高精度的初相位提取功能，满足DLA的检测要求。

3.2 非稳态信号检测精确度对比分析

频率变动会导致频谱间泄漏量的变化，将影响谐波参数估计的精度，仍采用第3.1节所使用的谐波信号进行频率变动下的仿真分析。由于DLA的测量精度主要取决于电压和电流初始相位的参数提取精度，因此下文着重于相位参数的比较分析。当基频在49.5～50.5 Hz之间变化时，采用Nuttall窗的插值校正算法作为对照组与所提算法共同用于估计信号的相位参数，相对误差如图8所示。当信号频率变动时，相位参数估计相对误差比信号频率不变动时降低约2个数量级，但检测精度远高于对照组算法，说明本文算法能够有效克服频率变动对信号相位参数估计精度的影响。

图8 频率变动时相位参数仿真结果的相对误差分布Fig.8 Relative error distribution of the simulation results of phase parameters in frequency variation

在实际运用时，信号中往往含有丰富的噪声，这会对信号分析准确度产生很大的影响。在信号模型上添加具有不同信噪比的白噪声，并分别选择Blackman窗、2阶HSCW窗的双线插值校正算法，8项余弦窗的四线插值校正算法为对照组，与本文算法进行仿真对比分析。信号基波相位参数的相对误差分布曲线结果如图9所示。

图9 白噪声下基波相位估计Fig.9 Fundamental phase estimation under white noise

由图9可见，由于Blackman单窗的旁瓣性能较差，在添加白噪声之后，基波信号的相位参数估计误差变化很大。当噪声强度较大，即信噪比(signal-noise ratio, SNR)小于30 dB时，相对误差变化均较大，但是本文算法仍占据明显优势。例如：当SNR为30 dB时，本文算法的参数提取精度为10-4%，基于8项弦余弦单窗算法的检测精度为10-3%；当噪声强度较小时(SNR不小于40 dB)，所有算法的相位估计误差均随着SNR的增大而不断减小。仿真结果表明：本文算法能有效抑制白噪声对基波相位参数估计精度的影响，误差变化明显低于其他算法。

4 应用与讨论

为了进一步验证基于CSCW的双线插值FFT DLA分析算法的有效性，在Simulink中搭建电容设备模型，并在注入谐波及加入白噪声等情况下进行仿真分析。使用工具箱提取数据，分别采用加Hamming窗、加4项3阶Nuttall窗、2阶三角形自卷积窗(triangular self-convolution window，TSCW)插值校正算法为对照组，与本文算法进行仿真对比分析。

4.1 信号基频变动时的仿真实验与分析

在实际电网中，频率在一定范围内有波动性，因此必须考虑频率波动对DLA测量精度的影响。有频率波动但是无谐波且无噪声时，电容型设备的等效电路和数字信号产生模型如图10所示，其中C=50 μF，R2=10 kΩ，根据计算式δ=ωR2C得到δ理论值为0.006 366 1 rad。设电压源如式(19)所示，频率在±0.2 Hz范围内波动，步长为0.1 Hz，采样点数为512，分析结果如图11所示。

U=311sin(50×2πft+30°) V.

(19)

图10 基波频率变动时的仿真电路Fig.10 Simulated circuit in fundamental frequency variation

由图11可知，相同条件下本文算法的测量精度比对照组算法高。例如频率在49.9 Hz时，本文算法测量误差约为10-9%，比TSCW插值算法高了4个数量级。基于Hanning窗插值算法检测精度

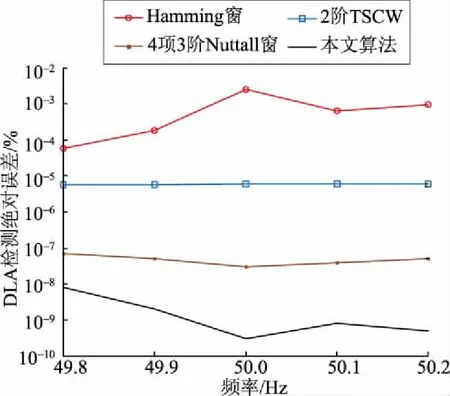
图11 基波频率变动时DLA检测值的绝对误差分布Fig.11 Absolute error distribution of DLA detection values in fundamental frequency variation

最低，在频偏较大时已产生严重检测误差。随着频率偏移，本文算法的DLA测量精度波动性较小。上述分析说明本文提出的算法克服了频率波动的影响，具有较高的DLA测量精度。

4.2 有谐波注入时的仿真实验与分析

在非同步采样的情况下，当待分析的信号中存在谐波分量时会发生谱干扰现象，增加DLA的测量误差。针对图12所示的仿真模型，采用式(20)的信号进行实验，设置同样的频率波动范围及变化步长，采样点数为512，仿真结果如图13所示。

U=[311sin(50×2πft+30°) +

0.01sin(150×2πft+45°)+

0.006sin(250×2πft+60°)] V.

(20)

由图13可以看出，当信号中存在谐波分量时，与第4.1节的检测结果相比，所有算法的测量精度均有所降低。如频率为50.1 Hz时，本文算法与基于Hamming窗插值算法的DLA检测误差值分别为10-9%和10-3%数量级，比无谐波干扰时均降低1个数量级。但横向比较，本文算法仍具有明显的精度优势。

图12 有谐波时的仿真电路Fig.12 Simulated circuit with harmonics

图13 注入谐波时DLA检测值的绝对误差分布Fig.13 Absolute error distribution of DLA detection values with harmonics

如果谐波注入比改变，则谐波对基波的泄漏量也会改变，进一步探讨谐波注入比例变化对DLA检测精度的影响。3次谐波占电压和电流谐波信号很大比例，因此将3次谐波的注入比例从0%提高至8%，并采用相同的仿真模型和测量方法，结果如图14所示。

图14 3次谐波注入比例变化对DLA测量的影响Fig.14 Influence of the 3th harmonic component on measurement of DLA

当3次谐波含量变化时，DLA测量误差也会发生变化。例如，基于4项3阶Nuttall窗插值校正算法在3次谐波比为8%时，检测精度降低约1个数量级。由于CSCW函数可以有效地抑制谐波对基波的泄漏干扰，本文算法测量精度高于其他算法，可以克服谐波成分变化对DLA测量精度的影响。

4.3 有白噪声时的仿真实验与分析

在非实验室条件下，噪声不可忽略，它会大幅降低DLA的测量精度。有噪声时电容型设备的等效电路如图15所示，在式(20)的信号中添加不同信躁比的白噪声，采用本文算法进行DLA测量。噪声是随机的，取100次测量的平均值以降低测量误差，分析结果如图16所示。

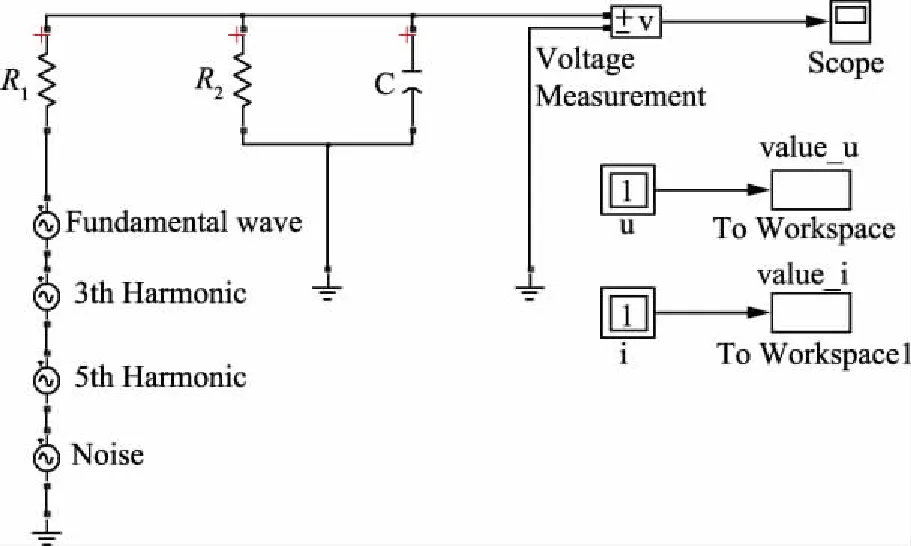
图15 有噪声时的仿真电路Fig.15 Simulated circuit with white noise

由图16可知，DLA的检测精度随着信噪比的不同而改变。当噪声强度较大时(SNR小于60 dB)，DLA测量误差较大，误差平均值约为10-2%～10-4%数量级；当噪声强度较小时(SNR不小于60 dB)，误差平均值小于10-6%数量级；本文算法误差随着信噪比的增大而不断减小。仿真结果表明，本文算法能有效抑制白噪声对DLA测量精度的影响。

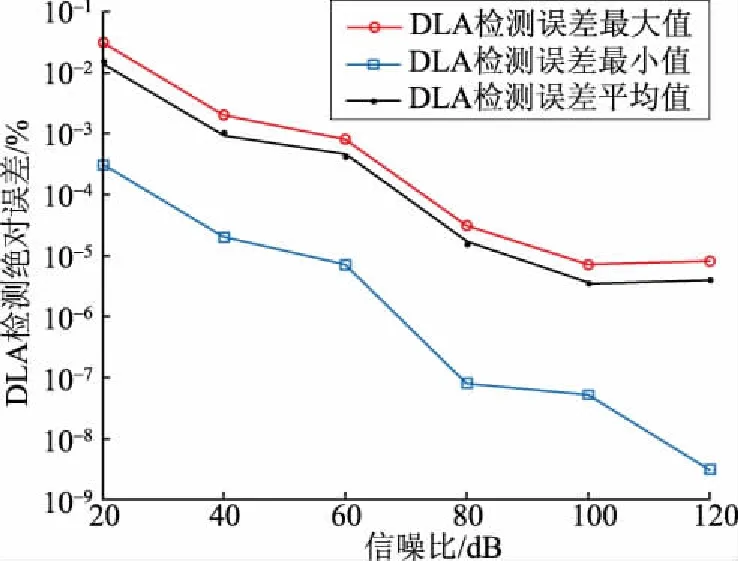
图16 存在白噪声时DLA检测值的绝对误差分布Fig.16 Absolute error distribution of DLA detection values with white noise

4.4 不同采样长度情况下的仿真实验与分析

信号采样长度对采用DFT算法的DLA测量结果有直接影响，增加采样点数可提高频率分辨率，同时伴随着计算量的增加。采用第4.1节的电路模型及电压信号进行仿真，设卷积窗长为256点、512点、1 024点、2 048点及4 096点对信号进行加权，DLA测量结果的绝对误差如图17所示。

图17 不同采样点数的DLA检测值的绝对误差分布Fig.17 Absolute error distribution of DLA detection values at different sampling points

由图17可知，采样点数为512时，DLA测量的绝对误差为10-10%数量级，满足检测要求，之后随着点数增加，测量精度不会显著提高；因此，当实际工程要求不是很高时，选择合适点数可以实现较高的计算精度，还可以减少计算量和分析延迟。

5 结束语

在非同步采样的情况下，频谱泄漏和栅栏效应会降低FFT对电容器件的DLA的测量精度，不能满足实际工程应用的需要。本文通过卷积运算，以8项余弦窗作为原始母窗构建p阶CSCW函数，所提出的窗函数具有比经典窗更好的旁瓣性能，并选用2阶CSCW对信号进行加权；然后基于双谱线插值原理，提出了一种加2阶CSCW函数的双谱线插值校正算法；利用MATLAB的polyfit函数求出插值校正公式，实现DLA的高精准测量分析。精度实验结果验证了本文算法的正确性和有效性，并且具有比其他算法更高的检测精度。最后，将本文算法应用于电容型设备的DLA测量并与对照组算法进行对比分析，结果表明该方法适合于DLA的精确测量。