一种基于DCM单元的高升压非隔离型DC/DC变换器
丁峰,王辉,李圣乾,杨剑,王寒
(三峡大学 电气与新能源学院,湖北 宜昌 443002)
目前,传统非可持续能源(如石油、天然气等)在全球能源消耗中依旧占主导地位,世界面临着资源匮乏、大气污染等诸多挑战,因此可再生能源的开发利用受到越来越多的研究和关注。其中太阳能源具有方便快捷、永不枯竭的特性,成为广大国内外研究学者的重点研究对象[1-5]。我国地域幅员辽阔,光照时间充足,更有利于光伏发电的研究与推广。
随着社会的高速发展,电力需求量越来越大,光伏发电进入全面规划研究阶段,呈现出良好的发展前景[6-11]。全球光伏系统的总装机容量到2020年将达到92 GW,光伏发电系统规模越来越大,系统总成本越来越高,而光伏系统中变换器的平均价格到2020年下降到0.09 元/W[12]。虽然光伏系统中变换器占总成本的十分之一左右,但变换器的性能关乎整个光伏系统的性能,其重要程度不言而喻[13]。在传统的光伏系统结构中,光伏电池组件经并联或串联后与DC/DC变换器相连,再由DC/DC变换器升压后,通过逆变器直接与电网或负载相连。该结构存在系统成本高、工作效率低、变换器使用数量多、输入输出增益低、器件应力高等缺点[14-20]。文献[21]提出的传统光伏系统结构包括集中型结构、组串型结构及多路组串型结构。集中型结构是先由多个光伏发电组件串联或者并联,再经过一个大功率的DC/AC变换器直接与电网相连;这种结构会引起电池组之间的不匹配,导致输出光伏模块的电压通常低于50 V。组串型结构是由多个光伏发电模块串联升压之后再与配套的逆变器相连,然后与电网或者负载相连;这种结构中某块光伏发电模块损坏将引起整个系统失灵,可靠性较低。多路组串型结构是在组串型结构中加入配套的DC/DC变换器,再通过公共的逆变器与电网或者负载相连;此类结构设计灵活,升压能力强,但仍然存在组串型结构可靠性低的缺点。为了解决以上问题,目前专家学者提出一种基于独立光伏组件的微型逆变系统,该系统与传统结构相比较具有效率高、可靠性高及系统成本低等特点。但是,无论哪种光伏发电结构,要想使系统结构最优,改善变换器的使用情况,用于光伏系统的变换器必须具备高升压能力。目前光伏系统中DC/DC变换器可分为隔离型与非隔离型。文献[22-23]提出了一种开关电容、电感变换器,此变换器效率高、集成度高,但是输入输出增益相对较低。文献[24]提出了一种谐振型变换器,该变换器功率密度高,系统利用率好,但控制策略相对复杂。文献[25]提出了一种隔离型DC/DC变换器,该变换器实现了零电压开通,提高了变换器效率;但是这种变换器使用了笨重的隔离变压器,增加了系统体积与成本,且引入了较大的漏感和寄生参数,引起变换器电压应力尖峰。文献[26]提出了一种改进的模块化多电平变换器,具有比传统模块化多电平变换器更多的输出电平数且无需滤波,降低了系统硬件成本。
本文提出了一种基于二极管-电容倍增器(diode-capacitor multiplier,DCM)单元的高升压非隔离型DC/DC变换器。首先对变换器的工作原理及工作性能进行阐述,然后通过仿真及实验对所提变换器具有的高输入输出增益、低器件应力及控制策略简单等优点进行验证,论述其在光伏发电系统的适用性,最后对变换器的损耗进行理论分析。
1 工作原理
变换器总拓扑如图1所示,图2是包含2组DCM单元的拓扑图,其中,uin为电源电压,L1—L4为输入电感,D1—D4为输入相二极管,C1、C2为输入相电容,S1、S2为开关管,C11—C1n、C21—C2n为DCM单元中电容,D11—D1n、D11—D2n为DCM单元中二极管,DO1、DO2为输出二极管,CO为输出电容,R为负载,uin、uout为输入、输出电压。为了便于分析,以下所有分析过程均作以下假设:①电感电流iL1、iL2、iL3、iL4连续;②所有电容容值足够大,忽略电容电压纹波影响。
本文采用交错并联控制,即开关管S1、S2相差180°导通,这种控制策略可以减小输入电流及其纹波影响。以图2为例,当开关S1导通、S2关断时,电感L3、L4,电容C2,二极管D21、D22,电容C11、C12构成给电容C11、C12充电的回路;当开关S2导通、S1关断时,电感L1、L2,电容C1,二极管D11、D12,电容C11、C12构成给电容C11、C12放电的回路。这样,电容C11、C12就实现了安秒平衡。同理,电容C21、C22也能实现安秒平衡,变换器实现了自动均流,省去了复杂的控制策略。
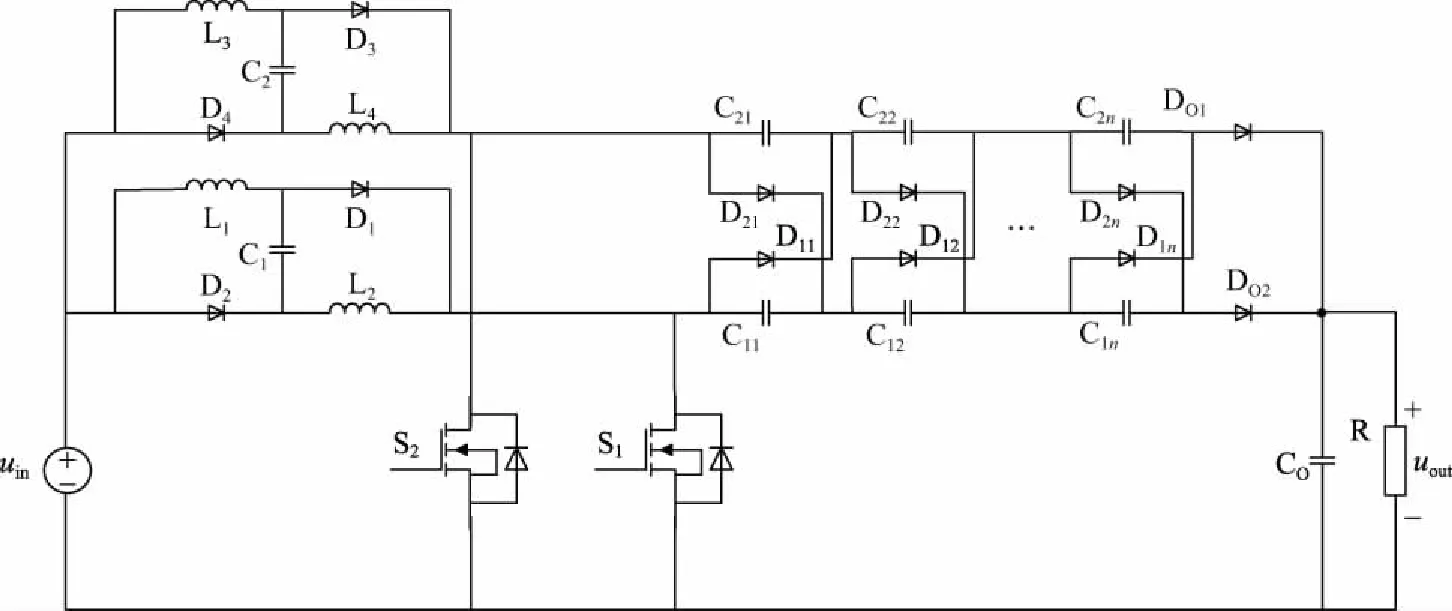
图1 变换器总拓扑Fig.1 General topology of the converter

图2 2组DCM拓扑Fig.2 2 sets of DCM topology
图3为变换器一个周期内的主要工作波形(占空比D=0.6),其中,uC11、uC12、uC21、uC22为DCM单元中电容电压,uS1、uS2为开关管电压,uD11、uD12、uD21、uD22为DCM单元中二极管电压,TS为总开关周期,DS1TS为开关管1开关周期,DS1为开关管S1的占空比,DS2TS为开关管2开关周期,DS2为开关管S2的占空比。

图3 一个开关周期内的主要波形Fig.3 Main waveforms in a switching cycle TS
图4为3种开关模态的等效电路。变换器工作模态如下:
开关模态1(t0—t1,t2—t3):开关S1、S2均导通,二极管D1—D4导通,其余二极管均关断;电感L1—L4充电,电容C1、C2充电;电流iL1、iL2、iL3、iL4均线性上升;输出电容CO单独给负载供电。
开关模态2(t1—t2):开关S1导通,S2关断,二极管D1、D2、D21、D22、DO1均导通,其余均关断;电感电流iL1、iL2继续上升,iL3、iL4线性下降,电感L3、L4,电容C2通过二极管D21、D22给电容C11、C12充电,同时又对电容C21、C22放电;电容电压uC11、uC12升高,电容电压uC21、uC22降低。
开关模态3(t3—t4):开关S2导通,S1关断,二极管D3、D4、D11、D12、DO2均导通,二极管D1、D2、D21、D22、DO1均关断;电感电流iL3、iL4线性上升,iL1、iL2线性下降,电感L1、L2,电容C1通过二极管D11、D12给电容C21、C22充电,同时又对电容C11、C12放电;电容电压uC21、uC22升高,电容电压uC11、uC12降低。此模态结束,开始下一个开关周期的工作。
2 性能分析与性能对比
本节根据上述变换器的工作模态,对所提变换器进行性能分析,将分析结果应用到n个DCM单元中,并将本文所提变换器与其他3种变换器的性能进行对比。
2.1 变换器输出增益
根据电感的伏秒平衡可得:
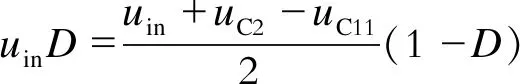
(1)
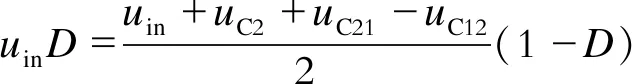
(2)
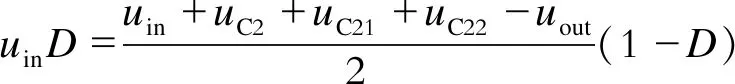
(3)
由开关模态1可得
uC1=uC2=uin.
(4)
由开关模态2可得
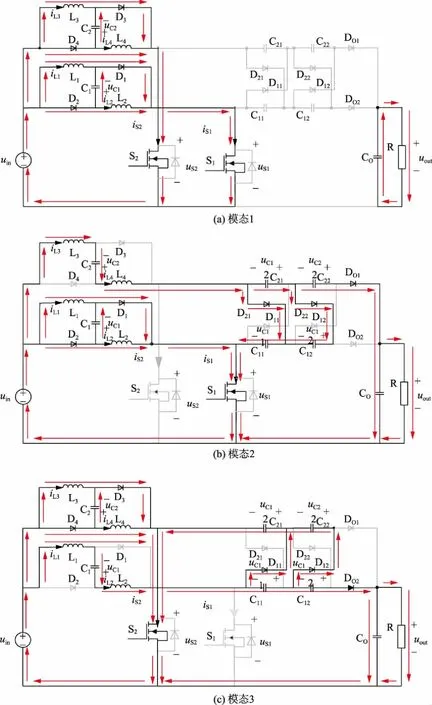
图4 3种开关模态的等效电路Fig.4 Equivalent circuits of three switching modes
uC21=uC12.
(5)
由开关模态3可得
uC11=uC22.
(6)
由式(1)—(4)可以得到

(7)

(8)
所提变换器的电压增益

(9)
同理,推广到n个DCM单元可得
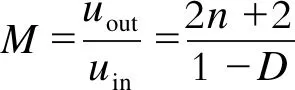
(10)
由式(10)可知,所提变换器的增益高且可调。
2.2 开关器件电压应力
根据图4所示变换器的工作原理及模态分析可知开关管电压应力

(11)
输出二极管DO1、DO2的电压应力
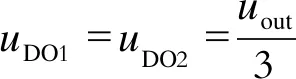
(12)
DCM单元中包含的二极管的电压应力
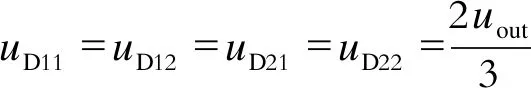
(13)
同理,应用到n个DCM单元可得

(14)
输出二极管DO1、DO2的电压应力

(15)
DCM单元中包含的二极管的电压应力
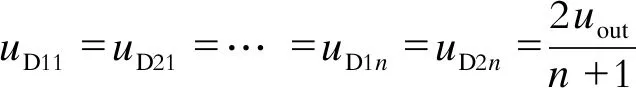
(16)
综上所述,与传统变换器相比,本文所提的基于n个DCM单元的变换器开关管及二极管的电压应力都得到了很大的降低,且可以随着DCM单元的变化调节,适用于对增益要求不同的场合,可以更自由地选择耐压较低的开关器件,降低变换器损耗,提高变换器效率。
2.3 开关器件电流应力
假设:①电感电流iL1、iL2、iL3、iL4连续,忽略纹波影响,设有效值分别为IL1、IL2、IL3、IL4;②本拓扑所有二极管电流均用平均值表示,且忽略其纹波影响;③输入电流平均值为Iin,忽略纹波影响。由DCM单元中电容的安秒平衡得:
IDO1(1-D)TS=ID12(1-D)TS.
(17)
IDO2(1-D)TS=ID22(1-D)TS.
(18)
(IDO2+ID12)(1-D)TS=(ID21+ID22)(1-D)TS.
(19)
(IDO1+ID22)(1-D)TS=(ID11+ID12)(1-D)TS.
(20)
由式(17)—(20)可得
ID11=ID12=ID21=ID22=IDO1=IDO2.
(21)
又有:
(22)
综上可得:
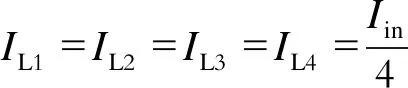
(23)

(24)
可知,电感电流实现了自动均流,不需要复杂的控制策略。
由上述分析,结合拓扑的工作原理易得开关管平均电流IS1、IS2为:
(25)
同理,推广到n个DCM单元可得:
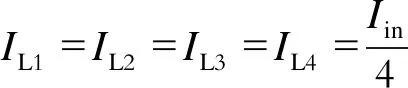
(26)

(27)
(28)
综上所述,本文所提变换器实现了自动均流,简化了控制策略。变换器输出增益高,开关器件电压、电流应力低,且随着DCM单元的变化而变化,变换器灵活,适用于高升压场合。
2.4 性能对比
本文所提变换器与其他3种变换器的对比见表1。

表1 本文变换器与其他3种变换器对比Tab.1 Comparison between the converter in this paper and the other three converters
由表1可知:本文所提变换器较其他3种变换器输入输出电压增益高;其他变换器虽然开关应力低,但所用开关器件多,变换器成本高,损耗大。因此,本文所提变换器较适用于光伏发电系统中的高输入输出增益场合。
该变换器与其他变换器相比较尚存在一些瑕疵。虽然该变换器在电压增益及器件应力方面存在优势,但在变换器利用率方面还有待提升。如目前应用于光伏发电中的多端口DC/DC变换器,该类变换器可连接若干个太阳能电池板,不仅可以实现资源的充分利用,还可以实现输入源的功率管理和控制。
3 仿真分析
本文基于PSIM搭建变换器仿真模型。基本仿真参数为:额定功率PO=600 W,输入电压uin=40 V,输出电压uout=600 V,负载R=600 Ω,开关频率fs=50 kHz,占空比D=0.6。主要器件选型为:电感值L1=L2=L3=L4=250 μH;电容值C1=C2=80 μF;DCM中电容值均为20 μF;输出电容值CO=50 μF。实验波形如图5所示。由图5(a)输入输出电压波形图可知,输入电压为 40 V,输出电压近似600 V,与理论值相似。由图 5(b)DCM单元中电容电压波形图可知,电容电压为200 V,与理论计算值一致。由图5(c)电感电流波形图可知,所有电感电流均为4.2 A,与理论值相似。L1、L3电流同相位,L2、L4电流同相位,且两两相差180°,符合开关管交错并联导通规则。由图5(d)开关管电压、电流波形图可知,2个开关管的电压应力均为200 V,为输出电压的1/3,与理论分析一致。由图5(e)二极管电压波形图可知,DCM单元中二极管电压均为400 V,与理论计算一致。由图5(f)二极管电压、电流波形图可知,二极管DO1、DO2电压均为200 V,二极管DO1、DO2电流均为2.5 A,与理论值相似。
4 实验样机关键参数计算
本节给出了所提变换器关键器件的参数计算。基本参数设定为:额定功率PO=300 W、开关频率fs=50 kHz、占空比D=0.6、负载R=300 Ω、输出电压uout=300 V、输出电流iout=1 A。则其输入电压uin=20 V、输入电流iin=15 A。
a)对于开关管:由第2节性能分析与性能对比可知,开关管电流iS=6.5 A、开关管电压uS=100 V;可见开关管电压为输出电压的1/3,有利于开关管的选型与散热器的设计。
b)对于二极管:由第2节性能分析与性能对比可知,二极管电流iD=2.5 A、二极管电压uD=200 V;二极管电压为输出电压的2/3,有利于二极管的选型与散热器的设计。
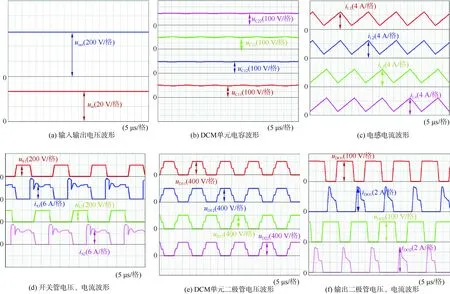
图5 仿真波形Fig.5 Simulationwaveforms

5 实验分析
为验证上述分析,搭建了额定功率PO=300 W的实验样机,基本参数为:输入电压uin=20 V,输出电压uout=300 V,负载R=300 Ω,开关频率fs=50 kHz,占空比D=0.6。主要器件选择为:电感L1=L2=L3=L4=250 μH;考虑到实验室电容规格,选取电容值C1=C2=40 μF;为设计电路简便,DCM中电容值均取为10 μF;输出电容值CO=50 μF。实验波形如图6所示。
由图6(a)输入输出电压波形图可知,输入电压为20 V,输出电压300 V,与理论值相似。由图6(b)DCM单元中电容电压波形图可知,电容电压均为100 V,与理论值一致。由图6(c)电感电流波形图可知,所有电感电流均为3.7 A,与理论值相似。由图6(d)开关管电压、电流波形图可知,2个开关管的电压应力均为100 V,为输出电压的1/3,与理论分析一致。由图6(e)二极管电压波形图可知,DCM单元中二极管电压均为200 V,与理论计算一致。由图6(f)二极管DO1、DO2电压、电流波形图可知,二极管DO1、DO2电压均为100 V,电流均为2.5 A,与理论值相似。图7是该变换器实测效率曲线,由图7可知,在输出功率为额定功率时效率最大为94.3%。
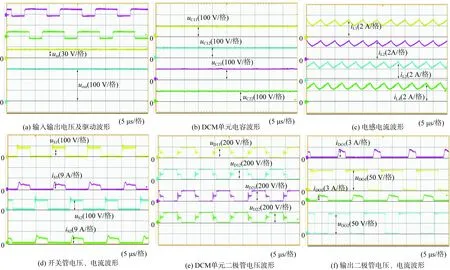
图6 实验波形Fig.6 Experimental waveforms

图7 效率曲线Fig.7 Efficiency curve
6 损耗分析
本节对变换器各元件进行了详细的损耗计算,给出了效率的理论分析值,计算所提变换器中每个器件的损耗,并给出各元件损耗占总损耗的百分比。
a)设PCON为所提变换器开关管的导通损耗,Ron为主开关管的导通电阻,Isrms为通过主开关管的电流有效值,则有:
Isrms=[(IL1+IL2)2D+
(IL1+IL2+ID21+ID22)2(1-D)]0.5=9.8 A.
(29)

(30)
b)开关管的开关损耗

(31)
式中:US为平均电压;IS为平均电流;tf为开关时间。
开关管的总损耗PS=PCON+PSW=8.3 W.
c)设PC为所提变换器电容损耗,因为电容本身存在导通时的电阻,会产生电阻的热效应,所以电容的损耗应该由其电流的有效值ICRMS来计算,即:
ICRMS=[(ID11+ID22)2(1-D)+
(ID12+IDo2)2(1-D)]0.5=3.3 A.
(32)

(33)
式中RSRC=6.9 mΩ为电容等效电阻。
d)所提变换器所有二极管的导通损耗
PDCON=10vFID=3.2 W.
(34)
式中:vF为二极管正向导通压降;ID为二极管平均电流。本文所选二极管为IDT12s60c,其反向恢复电流在工作时特别小,故忽略其反向恢复损耗。
e)设PL为所提变换器的电感损耗,电感选用KT157-45,其参数如下:磁心外径do=39.9 mm,磁心内径di=24.1 mm,磁心横截面积Ae=1.06 cm2,磁心体积V=10.7 cm3,电感因数AL=130 nH/N2(N为线圈匝数)。由本文第4节关键参数计算以及第5节实验分析可知所提变换器的开关频率fs=50 kHz,电感L=250 μH,电感电流为3.75 A,则其电流纹波
(35)
式中Imax为电感电流最大值。
线圈匝数

(36)
最大磁通密度

(37)
最大交流磁通密度

(38)
磁心损耗
PFe=VPL=1.39 W.
(39)
线圈损耗

(40)
电感损耗
PL=PFe+PCu=6.36 W.
(41)
f)设Pother为所提变换器的其他损耗。其他损耗包括导线损耗等,占总功率的0.5%。
本文所提变换器的效率理论值
η=Po·(Po+PCON+PSW+PDCON+
PC+PL+Pother)-1=93.6%.
(42)
综上所述,变换器在额定工况下效率最高为93.6%。
表2为主要功率器件损耗所占总损耗的百分比。由表2可知开关管损耗与电感损耗为本文所提变换器的主要损耗。

表2 损耗分析Tab.2 Power loss analysis
7 结论
本文提出一种基于DCM单元的高升压非隔离型DC/DC变换器,详细阐述了所提变换器的工作原理、工作模态、关键参数设计及各元件损耗计算,并通过仿真及300 W实验样机分析验证了该变换器的特性,结果表明:①该变换器具有很高的输入输出增益,在不同高升压应用场合,通过调节DCM单元数量即可改变输入输出增益及器件电压应力,适用于对增益要求不同的场合;②该变换器电感电流实现了自动均流,无需其他复杂控制策略;③与传统的变换器相比,该变换器开关管的电压、电流应力得到了较大的降低,器件选型容易。综上所述,该变换器输入输出增益高,器件应力低,控制策略简单,较适用于要求功率较高的光伏系统。

