考虑光伏无功分区计价的配电网无功优化

陆海强，吴秀英，周武，黄帅飞

(1. 嘉兴市恒创电力设备有限公司，浙江 嘉兴 314000；2. 南京旭电科技有限公司，江苏 南京 210012；3. 河海大学，江苏 南京 211100)

随着我国清洁能源市场日益完善，分布式发电装机容量稳步增长[1]，高渗透率的并网光伏(photovoltaic，PV)广泛接入到配电网之中，使原有的无功补偿设备的运行策略产生较大改变[2]。受源荷不确定性及线路参数较大影响，PV通过逆变器(inverter,INV)接入配电网后提供无功服务，配合原有无功调节设备进行联调优化，可降低有功网络损耗、减少电压越限，提升配电网运行的经济性[3-5]。传统并网PV有功功率控制方法，在并网点电压越限时增加/降低有功输出解决电压越限问题[6]，会带来严重的弃光问题，损害PV发电企业的利益。部分学者提出利用INV控制技术对光伏逆变器(photovoltaic inverter，PVINV)有功无功功率进行解耦控制，使INV按电网需求动态的发出/吸收无功功率进而调节电压[7-9]，但是在此策略下持续工作会导致INV过热，漏电流增大，不利于并网系统稳定运行。如文献[10]所述，采用INV优化调度(optimal inverter dispatch，OID)策略，可以减少弃光量，提高系统稳定性，但未考虑有载调压变压器(on-load tap changer，OLTC)的调节作用，且在运行中缺乏详细的无功分区控制策略，不利于无功市场的积极发展。

竞争电力市场环境中，无功服务对国家电网有序经营和社会稳定用电意义重大，需要通过市场竞争形成合理的无功定价，以形成规范化和科学化的辅助服务。在原有电容器(shunt capacity，SC)组、OLTC和静止无功补偿器(static var compensator, SVC)等无功调压设备的基础上，通过联调优化提升无功补偿设备的自动化水平，实现硬件资源的高效利用[11]。

文中对分布式PV网INV无功出力运行策略进行研究，考虑电力市场环境下无功成本，提出并网PV无功功率分区计价模型，构建含电力市场环境下考虑PV无功功率分区计价等多重主动管理措施的配电网无功优化模型；为求解混合整数二阶锥规划(mixed integer second order cone programming，MISOCP)模型，采用大M法等数学手段处理模型中的非线性项，考虑SC与OLTC的对偶变量采用奔德斯分解(Benders decomposition，BD)方法对模型分割求解；最后进行仿真验证。

1 并网PVINV调压及无功分区模型

1.1 PVINV无功分区方法

INV参与电压控制可提供不低于满载时(功率因数为0.9超前/滞后)的无功功率[12-13]。如图1所示，采用OID控制策略的PVINV可行域为O-A-B-C-D-E围成的区域。

图1 OID控制策略下PVINV的运行区域Fig.1 Operating region of PVINV under OID control strategy

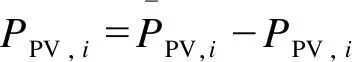
(1)

通过分析PV发电运行规律及其并网INV输出的P-Q容量曲线，本文对INV输出功率范围进行区域划分,即

(2)

式中：Qθmax、Qθlim分别为PVINV的最大功率因数角(点A、E)和最大容量约束角(点B、D)对应的无功功率。其中INV输出功率范围区域划分具体含义为：

a)区域OAB。QPV,i<0，调节无功出力时，会降低有功出力水平，为INV容量约束阶段，INV输出的容性无功功率随功率因数角增大而增大，满足-SPV,isinθmax≤QPV,i≤0，在A点达到无功最大值。若持续吸收大量无功可能引发INV过热、漏电流升高甚至引发电网无功波动和电压失稳。本运行区属于超额无功调节范围，为电力系统提供无功服务，降低有功出力收益，增大设备运行维护成本，电网需向PV电站支付无功服务费用与损失有功出力带来的机会成本。

b)区域OBC。QPV,i<0，INV从电网吸收无功功率，有功输出不受影响，在B点达到无功吸收上限，此时INV输出为最大功率Smax，功率因数角满足arccos(PPV,i/Smax)≤θi≤0；系统无功充裕时可参与无功优化降低无功电压，保障低负荷时段电网电压合格率并补偿线路电缆的充电功率，电网需向PV电站支付无功服务费用。

c)区域OCD。QPV,i>0，调节无功出力时，有功出力不受影响，可参与无功优化提高无功电压，在D点达到无功出力上限，INV输出为最大功率Smax，且0≤θi≤arccos(PPV,i/Smax)。此区域内INV无功出力除用于补偿PV运行时线路或升压变压器的无功损耗还向电网提供必要的无功支撑，需向PV电站支付无功服务费用。

d)区域ODE。QPV,i>0，调节无功出力时为INV容量约束阶段，会降低有功出力水平，INV输出的感性无功随功率因数角增大而增大，满足QPV,i≤SPV,isinθmax，在E点达到无功最大值。本运行区属于超额无功调节范围，需向PV发电站支付无功服务费与损失有功出力带来的机会成本。

1.2 市场环境下PVINV无功计价模型

并网PV参与无功优化的结构如图2所示。

图2 并网PV参与电力市场无功服务框架结构Fig.2 Structure of grid-connected PV participating in reactive power service in power market

本文在配电网无功优化运行时考虑并网PV在电力市场环境下的无功成本，竞争电力市场环境下无功定价是电力系统高效运行的关键因素[14]。以第1.1节分析为基础，结合无功电价理论得出竞争电力市场环境下PV无功辅助服务的无功分区定价方法[15]，PVINV各运行区域的无功价格表示为：

(3)

式中：CQ,PV为购买INV无功的成本；aOAB、aOBD、aODE和b分别为区域OAB、OBD、ODE的无功成本系数和损失有功的机会成本系数；ΔPPV,i,loss为保证无功功率输出而损失的有功功率。

2 考虑PV无功分区计价的配电网无功优化数学模型及其线性化

为方便对建立的数学模型线性化处理，定义

(4)

式中：Ui为节点i的电压幅值；Iij为流过支路ij的电流，形如下标ij的潮流参考方向为ij；N为网络节点集合。

2.1 目标函数

构建配电网日综合运维成本f最小为优化目标,即

minf=CQ+Closs+CU.

(5)

式中CQ、Closs、CU分别为无功成本、有功网络损耗和电压偏差成本。

无功综合运维成本CQ包括购买INV发出无功成本CQ,PV和原SC、OLTC的日运维成本CQ,VA：

CQ=CQ,PV+CQ,VA.

(6)

(7)

式中：cSC、cT分别为全寿命周期内SC、OLTC的单位调节代价；NSC,t为t时投入的电容器组数;NT,t为t时投入的OLTC档位;t为时间。

配电网络损耗成本为日内有功损耗成本,且

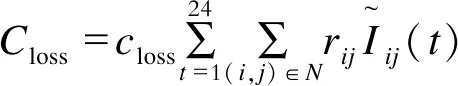
(8)

式中：rij为支路ij间电阻；closs为单位功率损耗成本系数；Δt为时间变化量。

将配电网络电压偏差成本进行松弛处理，即

(9)

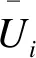
2.2 约束条件

2.2.1 配电系统潮流平衡与线路容量约束

采用distflow支路潮流方程满足等式约束：

(10)

QL,j-QPV,j-QSVC,i-QSC,j.

(11)

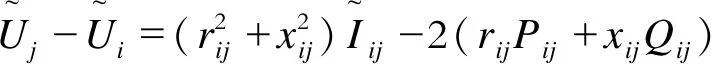
(12)

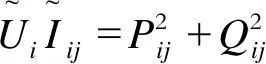
(13)

式中：j∈N;u(j)与v(j)分别为j节点的父节点集合和子节点集合；PL,j、QL,j分别为节点j负荷的有功功率与无功功率；Pij、Qij分别为对应支路ij有功功率与无功功率；PPV,j、QPV,j和QSC,j分别为节点j的PV有功出力、无功出力和SC无功出力；xij为支路ij上的电抗。

对二次方程进行松弛处理并转化为标准的SOC约束可得

(14)

松弛之后扩大了求解范围，保证其松弛为紧且仍可求得精确的最优解[16]。

系统安全运行不等式约束为：

(15)

式中：Ui,min、Ui,max分别为节点i电压的最小与最大值;Iij,max为支路ij电流的最大值。

2.2.2 常规无功控制变量及其约束

OLTC和SC是离散的无功电压调节设备，其动作指标为整数，为方便编码将其转换为0、1变量；同时从使用寿命、动作可靠性角度考虑，应限制其动作次数，并将其动作次数采用大M法等方式线性化处理。

设OLTC位于支路ij之间，在理想变压器与折算到高压侧的阻抗(线路阻抗与OLTC高压侧阻抗之和)之间设一虚拟点T0，电压为UT0。引入与分接头个数相等的nf个二进制变量ij,1，ij,2，…，σij, nf对应变比Tij{Tij,1，Tij,2，…，Tij, nf},同时引入较大正实数M1以及辅助变量hj,z。

(16)

OLTC操作次数去绝对值同式(9)处理类似，引入辅助变量Λk，转化为线性约束：

(17)

式中：σij,k(t)、σij,k(t-1)分别为t时段与t-1时段第k位二进制的状态取值；NT,lim,max为OLTC最大日动作次数限制。同一时刻有且仅有一个二进制变量能取1，相邻时段二进制变量差值的绝对值之和为2，则分接头动作，反之则无。

同理对于SC投入组数，引入一较大的正实数M2、辅助变量di,k、t时段二进制变量ε1i,t、ε2i,t和表示电容器投入组数的二进制数标志位δλi，可得：

(18)

(19)

式中：Ui、QSC,i、BSC,i、ΔBSC,i,0、KSC,i分别为节点i的电压、SC投入容量、SC投入电纳、单位SC电纳、电容器安装组数(可投入最大值)；kSC,i,t为t时刻第i组SC投入组数，满足式且ε1i,t⊕ε2i,t=1时SC动作，否则无动作；NSC,lim,max为SC最大日动作次数；λi为SC最大组数所需的最大二进制位数，KSC,i取8、9、16时，λi分别取3、4、4。

采用TCR-FC型的SVC作为动态、连续的无功补偿装置，以便更好地配合离散的SC组和谐波量较大的并网PV，减少设备投资，提高控制性能，满足约束：

QSVC,i,min≤QSVC,i≤QSVC,i,max.

(20)

式中：QSVC,i、QSVC,i,min、QSVC,i,max分别为安装在节点i的无功出力及其下限和上限值。

3 模型求解

3.1 模型的线性化

通过上述分析可知，模型中包含PV有功无功出力的连续变量，以及SC投切、OLTC分接头调整的离散变量，且潮流方程和目标函数存在非线性非凸函数，是一个混合整数非线性非凸的非确定性规划(non-deterministic programming，NP)模型，无法直接求解。综上，通过大M法[17]等技术将其转换为凸规划模型后，求解混合整数二阶锥规划问题，建立的市场环境下含并网PV的配电网有功无功优化MISOCP模型为：

(21)

3.2 模型的求解

二阶锥规划属于凸规划，虽可采用MATLAB/ GAMS等集成CPLEX、MOSEK求解器进行求解，但调试时间长。为提高复杂MISOCP模型的求解效率，采用BD法将模型分割为混合整数线性规划的主问题和二阶锥规划的子问题[18]。两者由Benders割相牵连，根据对偶原理，求主问题可得式的下界，求解子问题可获得其上界，交替迭代求解。其中子问题：

(22)

主问题：

(23)

式(22)、(23)中：Pr为引入的辅助变量；kSC,i,r、kij,r、ΘSC,i,r、Θij,r分别为SC、OLTC迭代r次的动作值及与其对应的对偶变量(相应函数依次类推)；fsub为子问题函数。

4 算例分析

4.1 网络结构与配置参数

采用基于IEEE-33节点改进的10 kV配电网架构验证本文优化模型和方法的正确性。改进后配电网总负荷为(3 720+j2 300) kVA，各节点负荷均值按日负荷预测曲线规律变化且各节点负荷功率因数不变。在节点1、2之间有5个档位装设OLTC，即[0，(1.0±2.5)%，(1.0±5)%]，日调节次数最大为4次。在末端节点18和33处分别接入 800 kW的分布式PV[19-22]，INV容量为842.10 kVA。PVINV运行区OBD无功输出范围为-262.95～262.95 kvar；运行区OAB、ODE无功输出范围为-484.32～484.32 kvar。PV并网点无功补偿在并网处分别接入容量为-200～300 kvar、-300～500 kvar的SVC。在节点8和节点25，分别配置单组容量为50 kvar的SC各25、15组，日投切次数最大为10次。网架结构、PV及无功调节设备安装位置如图3所示，其他计算用参数见表1。

图3 改进的IEEE-33网络拓扑结构图Fig.3 Improved IEEE-33 network topology

表1 结构与配置相关参数Tab.1 Structural and configuration parameters

为方便表示，简记以下4种方案：case1为未接入控制设备的基础对比计算方案；case2为考虑OLTC、SC、SVC调节的常规主动管理方案；case3为考虑PV无功出力与OLTC、SC、SVC调节的有功-无功协调优化方案；case4为考虑PV无功出力分区计价与OLTC、SC、SVC调节成本，响应电力市场下无功成本的有功-无功协调优化方案，即本文所提模型的优化方案。

4.2 不同策略下的配电网综合运维成本

通过仿真分析，得到不同运行策略下的优化结果见表2。

由表2可知：采用无功调节设备进行主动的无功电压调节可以降低系统的网络损耗28.49%和各节点同一时刻的电压偏移总和3.45%。计及PVINV的无功出力后，可在一定程度上降低无功调节设备调节次数，提升SVC备用容量并减少节点电压偏差，提高电能质量。为方便表示，选取PVINV的无功出力前后节点33电压分布与节点18处SVC运行状态如图4所示。虽然case3增加了部分无功备用，但是存在PVINV无功出力过大或不出力的情况，即运行区间不合理。

表2 不同运行策略下的优化结果Tab.2 Optimized results under different operation strategies

图4 case3节点33电压与SVC运行状态Fig.4 Node 33 voltage and SVC operating state in case3

采用考虑INV无功出力分区计价的无功成本优化控制后，减少INV持续大功率无功出力的时间，进一步提高系统稳定性和经济性。采用PV无功分区计价策略前后PV1-Q、SVC1的无功出力与SC1、SC2投入组数分别如图5，图6所示。

图5 case4下PVINV与SVC的无功出力Fig.5 Reactive power output of PVINV and SVC in case4

引入INV无功分区计价后，节点18的PVINV运行区域由OAB、ODE移动到区域OBD，避免了INV无功功率变化幅度过大、过频现象的发生，提高了系统安全稳定性。优化模型的目标函数计及无功成本，能够较好地解决高渗透率PV接入下节点电压越限问题，满足电压质量要求的同时减少了离散设备动作次数，增加离散设备使用寿命。在保证PV电站电力生产顺利进行的同时，减少了系统无功购买成本和PV电站设备的维护费用，有利于电力生产商积极参与无功市场建设。方案case3和case4的PV利用率分别为99.45%、98.67%，弃光率略微增加，但提高了系统和设备的安全经济运行能力，采用PV无功分区计价策略后网损与PV有功功率消纳情况如图7所示。

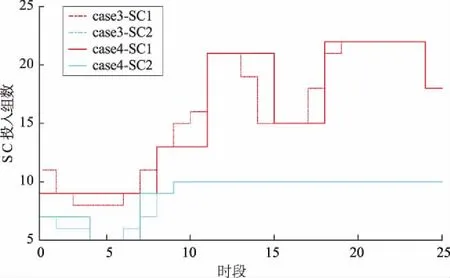
图6 case4与case3的SC的投入组数Fig.6 Input groups of SC in case4 and case3

图7 case4下网损与PV消纳情况Fig.7 Network loss and PV absorption in case4

不同优化模型计算时间见表3。

表3 模型求解对比Tab.3 Comparisons of model solutions

从表3可知：为了求解MINLP问题，在无功优化领域大量应用启发式智能算法，虽少于采用MOSEK算法所消耗的时间，但是并不能保证其为全局最优解，同时存在早熟问题；采用SOCP松弛线性化后的BD法将复杂MINLP拆解为2个简单模型，计算速度提高明显。

5 结束语

本文构建的电力市场环境下考虑PV无功功率分区计价的配电网有功-无功协调优化模型，计及了配电网运维综合成本，响应了PVINV无功分区计价、离散补偿设备操作次数和连续性无功设备的协调控制，保证了PV电站电力生产与配电网系统的安全稳定运行。有效调动PV电站积极参与无功市场竞争，可以合理并协调利用PVINV无功容量与配电网原有离散设备的无功支撑能力，保证用户电压质量，减少OLTC、SC操作成本，增加SVC备用容量。在模型求解方面，采用线性化手段，将复杂且不易求解的混合整数分线性优化模型线性化为MISOCP模型，并提出了基于BD法的求解策略，减少了计算复杂度，提高计算速度，有利于工程实际应用。