基于电力弹簧的微电网分布式发电协同控制
李天慧,周杨,张健,吕潇,马刚
(南京师范大学,江苏 南京 210023)
为了降低新能源发电并网对电网造成的不良影响并提高其利用率,美国电力可靠性技术解决方案联合会(Consortium for Electric Reliability Technology Solutions,CERTS)提出了微电网的概念:微电网是一种集成分布式能源、储能、能量转换装置、本地负荷以及能量管理系统的小型低压发配电系统,既可离网运行,也可并网运行[1-2]。目前在微电网控制技术方面的研究主要体现在保证系统的稳定运行方面[3-5]。文献[6]提出了基于协调控制器的微电网改进下垂控制策略,可以实现微电网有功负荷与无功负荷的优化配置;文献[7]提出一种不依赖于下垂控制的微电网协作二级控制策略,但该控制策略在通信网络出现故障时并不适用;为了避免通信问题,文献[8]设计了一种基于共识意识的分布式协调控制器,用于实现微电网中的电压调节以及无功功率共享,但是最终无法精确调节电压。
电力弹簧(electeic springs,ES)的概念在2012年由香港大学的许树源教授首次提出[9]。ES是一种能够快速实现需求响应的新技术,可以调节间歇性可再生能源接入大电网引起的系统波动问题[10],大量研究已经证实单个ES对配电网稳定电压[11-12]和改善电能质量[13-14]的作用。为了更好地应用ES解决电网存在的问题,越来越多学者开始研究多个ES接入对系统稳定性的影响,以及多个ES接入系统的协同控制策略。文献[15]介绍了一种动态的模块化ES模型用于调节智能电网的电压,提供了基于多个ES接入电网的实验结果。为了保证极端情况下关键性负载的快速恢复供电,文献[16]提出一种利用ES增强微电网与可再生能源弹性的控制策略。
由国内外已有的研究可以设想,如果ES大量应用在微电网中,可以为未来智能电网的发展提供强大支持。然而随着ES的应用,一方面,如果不能很好地协调接入微电网中的多个ES,可能给电网运行带来严重风险;另一方面,目前大多数学者仅从电压和频率调节中的一个角度进行考虑,无法实现电压和频率的同时有效控制。因此,本文建立了ES的有功/无功控制模型用于功率补偿,基于此,提出ES的四象限特性理论,用以设计ES的有功/无功综合控制模型;设计了基于PI控制器的ES有功/无功协同控制方法;考虑到传统下垂控制引起的误差以及集中控制的通信成本问题,提出一种基于离散一致性算法的分布式控制策略,以实现精确的电压和频率控制,并达到良好的动态响应效果;最后,建立了基于MATLAB/Simulink的九总线微电网系统模型,对比分析在电压突变、分布式发电功率突变、非关键性负载功率突变3种情况下,有无ES接入的系统电压和频率波动情况。
1 ES工作原理
ES是一种可以提供电压支持、电能储存以及抑制电压波动的电力装置[17],其基本结构如图1虚线框内所示,由2个单相半桥逆变器和1个电容电感(LC)低通滤波器组成。其中,Lf和Cf分别为低通滤波器中的电感和电容,US为系统电压,UNC为非关键性负载(non-critical load,NCL)两端电压幅值,Io为流过NCL的电流,Ic为电容电流,If为流过低通滤波器的电感电流,φNC为NCL阻抗角,ZNC为NCL阻抗。1号变流器作为分流补偿器,并联在电路中控制直流链路上的电压Udc;2号变流器作为串联补偿器,控制ES注入系统的电压UES和相位角θES,1号变流器与2号变流器通过公共直流链路进行双向功率流交换,保证实时功率平衡以实现电压稳定。
按照负载工作电压可承受的偏移程度,将负载分为关键性负载(critical load,CL)和NCL,后者主要包括家用热水器、照明系统、风扇、烤箱、洗碗机、干燥机等小型电动机负载。如图2所示,将ES与NCL串联构成智能负载(smart load,SL),并将其与CL并联,通过使能开关S控制ES工作。系统正常运行时,电网电压US为额定电压,为了保证NCL消耗的有功功率为定值,将ES充当串联功率补偿器,提供可变的交流电压,从而通过改变NCL两端的电压来保证CL两侧的电压和输送功率基本恒定。这就将供电方法由传统的用电量决定发电量模式调整为跟随供电量大小来实时改变负载的用电量模式。
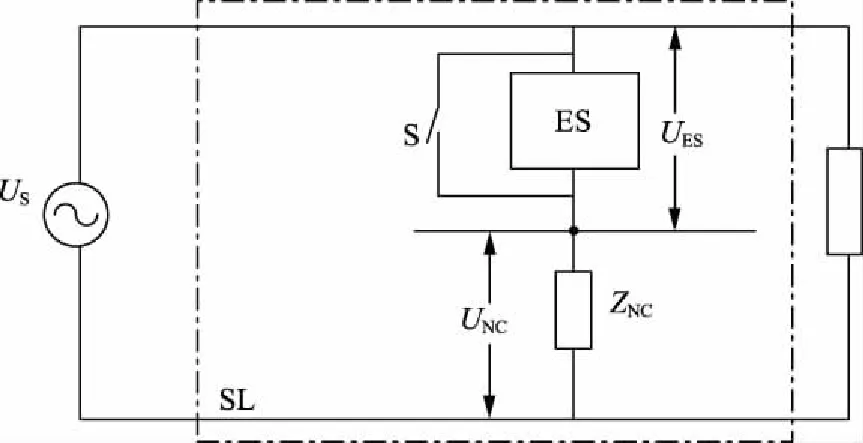
图2 SL简化电路Fig.2 Simplified circuit of SL
2 ES功率控制模型
结合图2,依据基尔霍夫定律,可将UES、US、UNC的关系表示为:
US∠θS=UES∠θES+UNC∠φNC.
(1)
式中θS为电源电压相位角。三角变化后可表示为

(2)
流过NCL的电流可以表示为
Io=UNC/ZNC.
(3)
SL的有功/无功功率可分别表示为
(4)
式中:PNC和QNC分别为NCL的有功和无功功率;PES和QES分别为ES的有功和无功功率。
2.1 ES无功控制模型
当以调节无功功率为目标控制ES时,可将其作为无功调节装置用以吸收或发出多余的无功功率,调节NCL的输出电压超前其支路电流90°/-90°,相量关系如图3所示。其中,USL为SL两端电压。

图3 ES无功控制相量关系Fig.3 Phasor diagram of ES reactive power control
当ES只工作在无功控制模式下时,此时其不消耗有功,即PES=0,SL有功功率

(5)
当θES为90°时,SL的无功功率
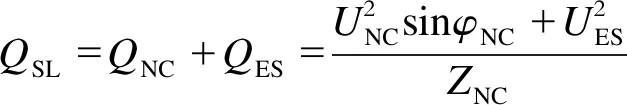
(6)
当θES为-90°时,SL的无功功率

(7)
根据式(6)和式(7)可以得到ES的无功功率控制模型为:
(8)
式中:QSL,0为ES未受控时的无功功率;ΔQ为ES的无功控制变量。根据式(8)和图3可知,当ΔQ>0时,表示ES的无功消耗量增大,此时控制θES为90°;当ΔQ<0时,表示ES无功消耗量减小,此时控制θES为-90°。
2.2 ES有功控制模型
当以调节有功功率为目标控制SL时,可将ES作为有功调节装置,用以吸收或发出多余的有功功率,调节NCL的输出电压超前其支路电流0°/180°,相量关系如图4所示。
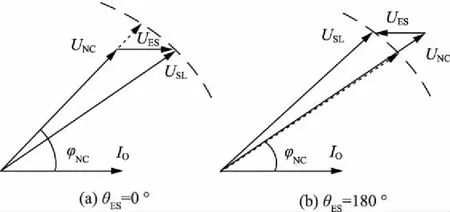
图4 ES有功控制相量关系Fig.4 Phasor diagram of ES active power control
当ES只工作在有功控制模式下时,此时其不消耗无功,即QES=0,SL无功功率

(9)
当θES为0°时,SL有功功率

(10)
当θES为180°时,SL有功功率

(11)
根据式(10)和式(11)可以得到ES的有功功率控制模型

(12)
式中:PSL,0为ES未受控时的有功功率;ΔP为ES的无功控制变量。根据式(12)和图4,当ΔP>0时,表示ES的有功消耗量增大,此时控制θES为180°;当ΔP<0时,表示ES的有功消耗量减小,此时控制θES为0°。
3 基于ES的微电网分布式控制方法
3.1 ES四象限特性
由第2章分析可知,可以根据电网对ΔQ、ΔP的要求,调节ES的电压幅值UES以及阻抗角θES,以减少任何突然增大或减少的电源及负载产生的不平衡;因此,为了充分利用ES有功和无功可以同时控制的特性,以此为标准划分4个象限,相量关系如图5所示,其中,UNC,0表示ES未受控时NCL两端的电压。

图5 ES四象限相量图Fig.5 Phasor diagram of ES four quadrant
依据有功/无功需求控制量ΔP、ΔQ的大小,结合第2章的分析,将ES对应的工作在图5中的4种工作状态下:
①当ΔP<0且ΔQ<0时,选择图5(a)的工作模式,实现SL有功功率的降低以及SL无功功率的提高;
②当ΔP<0且ΔQ>0时,选择图5(b)的工作模式,实现SL有功/无功功率的提高;
③当ΔP>0且ΔQ>0时,选择图5(c)的工作模式,实现SL有功功率的提高以及SL无功功率的降低;
④当ΔP>0且ΔQ<0时,选择图5(d)的工作模式,实现SL有功/无功功率的降低。
3.2 基于PI控制器的ES有功/无功协同控制策略
传统无功补偿装置采用的是输出电压控制技术,通过提供负载所消耗的无功功率,减少电网中无功功率流动,进而起到保持电网中无功功率恒定的作用。区别于此,ES采用输入电压控制技术,通过对ES本身的控制提供可变的交流电压;与此同时,在NCL中同时形成跟随电力系统波动而变化的可用功率,将分布式新能源接入及电网供电负荷造成的波动功率由NCL进行消纳,进而保证CL两端电压和功率维持稳定。参考文献[18],基于PI控制的ES控制结构如图6所示,其中Ua半桥逆变电路的输出电压,US,ref为电网参考电压,通过控制脉冲宽度调制(pulse width modulation,PWM)逆变器的电压调制系数m,可以产生基于线路频率的高质量PWM电压波形;通过使用LC滤波器,可以生成具有可控幅度的正弦电压UES作为电容电感滤波器的输出。

图6 ES控制结构Fig.6 ES control structure
假设2个半桥逆变器均工作在理想的无损功率模式下,根据图1、图6以及第2节分析可以得出逆变器直流环节输入功率和逆变器交流输出功率的关系如下:
(13)
依据基尔霍夫定律的半桥逆变变流器的数学模型如下:
(14)
半桥逆变电路的输出电压

(15)
电压调制系数

(16)
式中:Lf为LC滤波器电感;G(t)为补偿函数;UPWM为PWM三角形载波的电压幅值;US,ref通常选择额定电压220 V。
典型ES的基本控制回路如图7所示[19]。理论上该控制回路仅可以调节电网的无功功率,无法调节有功功率,但在实际运行中,由于功率逆变器和LC滤波器的功率损耗,将消耗少量的有功功率,从而达到调节有功功率的效果。为了达到更好的综合控制效果,本文改进图7所示的控制回路,调整后的控制回路如图8所示。
图8中:abs为取绝对值函数,PNC,ref为NCL的额定有功功率,QNC,ref为NCL的额定无功功率;k1、k2为PI控制器的后置增益,将UES分解为与IES同轴的UES-P分量以及与IES垂直的UES-Q分量;其中,UES-P相当于UES中作用于有功控制的分量,UES-Q相当于UES中作用于无功控制的分量;α和β为θES分解出来的2个分量,具体表示为

(17)
依据PI控制器的输出量a和b的正负决定查询表内的工作模式,当a>0且b<0时,工作在α=0°模式下;当a<0且b<0时,工作在α=90°模式下;当a<0且b>0时,工作在α=180°模式下;当a>0且b>0时,工作在α=270°模式下。
3.3 基于共识控制的离散一致性算法
上文针对单个ES的控制策略进行了研究,而在具有分布式发电和多个ES的微电网中,要解决的主要问题是如何协调安装在电网中的多个电力电子设备,并实现多个ES的分布式协同控制。因此,开发了一种基于代理(Agent)的分布式控制方法,该方法可以实现ES的即插即用,并且单个ES的故障不会影响系统的整体稳定运行。简化的微电网拓扑模型如图9所示,为每个ES分配1个代理负责,该代理可以通过跨越ES的通信流来获取本地信息,以便于不依赖于通信技术实现数据交换。

图7 基于PI控制器的ES控制回路Fig.7 ES control loop based on PI controller

图8 基于PI控制器的ES有功/无功协同控制回路Fig.8 ES active power and reactive power control loop based on PI controller

图9 微电网简化模型Fig.9 Simplified model of microgrid
分布式控制能够使得每个ES都可以访问其本地电压和功率流信息,但无法获取全局信息;为了解决这一问题,引入基于离散一致性算法的共识控制,以获得分配给图8中设计的ES控制器的参考功率。离散形式的一致性共识算法表述为

(18)
式中:k为一致性算法的迭代次数;n为微电网中的代理数量;aij为从节点i到节点j的数据传输通信权重,对于离散系统,aij=1表示j和代理i相邻,aij=0表示i与j没有相邻。在这种情况下,每个ES被视为1个代理,如果某个代理不与其他代理交换信息,则此代理保持其当前信息状态不变。一致性理论旨在确保基于代理的本地信息以分布式模式进行信息交换[20]后,代理可以根据从邻居收集的信息状态更新其信息状态[21]。设计以更新法则作为控制目标,使得所有代理的信息状态收敛到一个共同的值的一致性算法,用于协商达成共识代理,并提供系统的共识机制来计算共识值。离散一致性算法的流程图如图10所示。
如图10所示,首先,通过共识算法发现ES的功率参考值xi并进行初始化;然后,基于公式(18),通过相邻ES之间的信息交换,不断更新所需要的ES功率;最后,获得分配给图8中ES控制回路的基准有功功率PNC,ref和无功功率QNC,ref。

图10 基于离散一致性算法的共识控制流程Fig.10 Consensus control flow chart based on discrete consistency algorithm
对于整个微电网来说,全局信息发现过程可以用矩阵形式表现为
Xk+1=DXk.
(19)
式中:Xk和Xk+1表示在第k次和(k+1)次迭代时获取的信息量,X在本文中表示需要获取的基准功率,其中Xk=[x1,k…xi,k…xn,k]表示Xk内的元素;D为通信网络的权重矩阵,D=1-εL,其中ε为边缘权重系数,L为通信网络的拉普拉斯矩阵。将D表示为:

(20)
式中:nn表示第n个代理附近的代理量,为了适应ES的即插即用引起的网络拓扑变化,aij可以表示为
(21)
式中:nj和nj分别表示代理i和j附近的代理量;j∈ni表示j与i相邻。XES表示为

(22)
4 仿真验证
4.1 仿真模型
建立如图11所示的九总线系统微电网仿真模型,其中,系统的额定电压为35 kV,G1、G2和G3的额定功率分别为8 MVA、6 MVA和4 MVA;3个ES分别安装在总线5、总线6和总线8上,每个ES并联1个旁路开关,旁路开关在正常运行期间保持关闭状态,当需要启动ES时在0.1 s内打开。

图11 基于3个ES的九总线系统Fig.11 Nine-bus system with three ESs
根据图11建立的微电网仿真模型,通信网络的拉普拉斯矩阵表示为

(23)
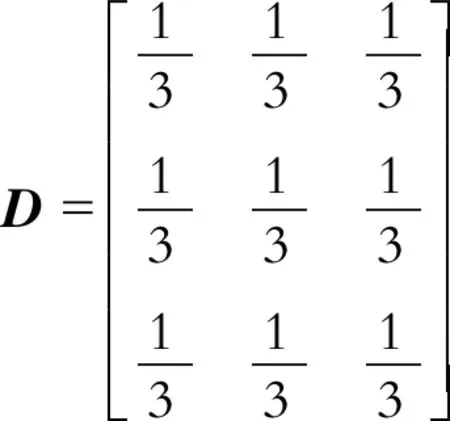
(24)
图11中,发电机和网络数据参考文献[22]选取,仿真模型具体参数见表1。

表1 仿真模型具体参数Tab.1 Specific parameters of simulation model
4.2 仿真试验及结果分析
4.2.1 试验1,母线电压突变
4.2.1.1 单母线电压突变
研究在重负载情况下,单条母线电压突变对有无ES接入微电网的影响,仿真模拟时间为30 s。当母线5处的电压U5骤降至210 V时,基于离散一致性算法的分布式控制平均电压迭代过程如图12(a)所示;在时间t=5 s时接入ES后,U5如图12(b)所示。

图12 单条母线电压骤降情况下的仿真波形Fig.12 Simulation waveforms in the case of single bus voltage dips
如图12可知:当U5骤降至210 V后,未接入ES时,U5在210 V左右波动;当在5 s时接入ES后,U5立刻上升至220 V,并在1 s内维持电压稳定。
4.2.1.2 多母线电压同时突变
研究在重负载情况下,多条母线电压突变对有无ES接入微电网的影响,仿真模拟时间为30 s。当母线6和母线8处的电压U6和U8同时骤降至200 V后,在t=5 s时接入ES后U6和U8如图13所示。
如图13可知:当U6和U8骤降至200 V后,未接入ES时,U6和U8均在200 V左右波动;当

图13 多条母线电压骤降情况下的仿真波形Fig.12 Simulation waveforms in the case of multiple bus voltage dips
在5 s时接入ES后,相较于单母线故障,多母线同时发生电压骤降时,ES接入的调节效果减弱,但仍能在1 s内将故障母线的电压维持在220(1±1%) V内。
通过试验1可知:当微电网中单个或多个母线电压骤降时,通过ES的应用,可以对发生故障的母线起到良好的支撑作用,并使其快速恢复到电压参考值,保证微电网的可靠运行。
4.2.2 试验2,分布式发电功率突变
保持负载功率不变,研究分布式发电输出功率发生变化对有无ES接入微电网的影响,仿真模拟时间为30 s。在t=10 s时,将风速从10 m/s升至16 m/s,风力涡轮机G1的输出功率有所增加,如图14所示,比较有无ES接入时,母线5上的电压变化及系统频率响应。
当分布式发电的输出功率上升时,如图14(a)所示:在没有接入ES的情况下,母线电压增加至224 V;接入ES后,发生短暂波动后可在0.5 s内将母线处的电压稳定在220 V。如图14(b)所示:当风速由10 m/s升至16 m/s时,在不接入ES的情况下,系统频率由于功率增加上升至50.8 Hz,根据相关标准[23],当电网频率超出49.5 ~50.2 Hz的范围时,连接在中低压系统中的电源应在0.2 s时与配电网断开;为了避免这一情况的出现,将ES接入电网,观察可知,系统频率能够快速恢复至50 Hz,并维持稳定。

图14 分布式发电功率突变下的仿真波形Fig.14 Simulation waveforms in the case of distributed power generation mutation
由试验结果可知:通过ES的应用,可以减轻由于分布式发电输出功率变化造成的系统电压和频率波动,将母线电压以及系统频率快速恢复至参考值,保证系统的稳定运行。
4.2.3 试验3:负载功率突变
保持分布式发电的输出功率不变,研究负载发生变化对有无ES接入微电网的影响,仿真模拟时间为30 s。在t=10 s时将母线5上NCL2的有功功率从3 MW升至4 MW,如图15所示,比较母线5上的电压变化及系统频率响应。
当负载的有功功率降低时,如图15(a)所示:在没有ES接入的情况下,母线电压降低至216 V;接入ES后,系统发生短暂波动后可在0.5 s内将母线处的电压稳定在220 V,偏差不超过1%。如图15(b)所示:当NCL的有功功率上升时,系统频率由于功率增加下降至49.5 Hz,当ES接入运行后,可以清楚发现系统频率能够快速恢复至50 Hz,并快速维持稳定。
由试验结果可知:通过ES的应用,可以减轻由于负载增加造成的电压和频率波动,将母线电压以及系统频率快速恢复至参考值,使风力涡轮机可以在系统中持续运行。

图15 负载功率突变下的仿真波形Fig.15 Simulation waveforms in the case of load power mutation
5 结论
本文提出一种基于ES的微电网分布式发电协同控制方法,并通过九总线微电网仿真模型模拟在母线电压突变、分布式发电功率突变、负载功率突变这3种情况下该方法的可行性,研究有无ES接入对微电网系统稳定性的影响。仿真结果表明:ES可以通过同时进行有功/无功补偿来有效解决微电网中分布式电源和负载变化引起的电压、频率波动,起到支撑线电压、动态平衡分布式能源和负载功率的作用,保证微电网的稳定运行。
相较于已有研究,本文所述方法的优势有:①通过调节信号的偏移角和幅值来实现ES的有功/无功同时控制,保证了电网电压和频率稳定,提高了电能质量;②设计了一种以更新法则作为控制目标,使得所有信息状态收敛到一个共同值的一致性算法为基础的分布式控制方法,提高控制精度的同时降低了通信干扰。在之后的研究中,一方面由于本文所使用的微电网仿真模型较为简单,并不能很好地反映实际微电网的电力特性,进一步的工作将会考虑选取实际的小型微电网作为仿真试点;另一方面,将进行算法改进,集中在优化通信网络方面,以达到加快信息发现过程的目的。

