基于流挖掘的分布式驱动电动汽车横向稳定控制＊

刘聪 陈勇,2 赵理,2

（1.北京信息科技大学，北京 100192；2.北京电动车辆协同创新中心，北京 100192）

主题词：电动汽车 转向状态预测 稳定性控制 流挖掘 马尔可夫模型

1 前言

分布式驱动电动汽车每个轮毂电机独立可控，通过合理分配各驱动轮的驱、制动力，可实现横向稳定性控制[1-3]。近年来，针对分布式驱动电动汽车横向稳定性控制，国内外学者已取得大量的研究成果。X.J.Jin等设计了一种鲁棒增益调度H∞控制器，通过跟踪理想横摆角速度和质心侧偏角产生附加横摆力矩实现横向稳定性控制[4]。林程等采用高阶滑模控制器，以变量误差和误差变化率作为控制对象，有效提高了汽车的操纵稳定性[5]。考虑到驾驶员行为与执行机构之间存在时间延迟，模型预测控制（Model Prective Control，MPC）采用滚动优化及反馈校正的方法预测未来一段时间内系统状态，计算目标函数的最优解，预测系统未来的输出，在车辆横向稳定性控制方面已有大量理论研究[6-11]。但MPC运算复杂，对硬件要求高，将极大地增加整车开发成本，同时，在车辆高频控制领域上难以保证精确的实时预测性。

本文针对分布式驱动电动汽车，提出一种基于转向状态预测的稳定性分层控制策略。运用滑模控制理论计算当前时刻施加的横摆力矩，基于流挖掘技术及马尔可夫模型预测下一时刻转向状态，模糊控制器根据预测值决策附加横摆力矩需求。采用前、后轴动态载荷转移方法，基于总期望横摆力矩实现各车轮驱动转矩的合理分配。

2 车辆动力学模型

如图1所示，利用线性二自由度的车辆模型进行控制器的设计，该模型能代表转向操纵稳定性的基本特征[12]，包括侧向运动和横摆运动。图1中，β为质心侧偏角；wr为横摆角速度；a、b分别为质心与前、后轴的距离；δ为前轮转角；L=a+b为轴距；u、v分别为车辆纵向、侧向速度；af、ar分别为前、后轮侧偏角；Fyf、Fyr分别为前、后轮受到的侧向力。

图1 二自由度汽车模型

基于二自由度车辆模型，侧向运动和横摆运动的表达式为：

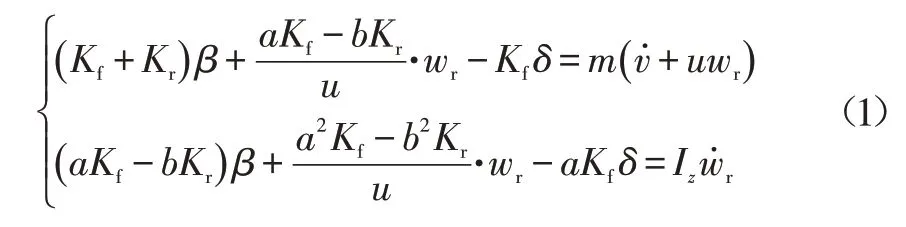
式中，Kf、Kr分别为前、后轮的侧偏刚度；β为质心侧偏角；m为整车质量；Iz为整车绕z轴的转动惯量。

当车辆进入稳态时，横摆角速度wr和质心侧偏角β均为定值，此时，wr=0，β=0，理想横摆角速度wrq和质心侧偏角βq分别为：

式中，K为稳定性因数。

车辆转向过程中，侧向加速度受到轮胎在路面上附着能力的限制，不能超过路面所能提供的侧向加速度极限值。因此，理想横摆角速度需满足：

式中，μ为路面附着系数；g为重力加速度。

综上，理想横摆角速度的限定值为：

当车辆进入稳态响应时，横摆角速度wr为定值，此时v=0、wr=0，代入式（1）得到稳态横摆角速度增益为：

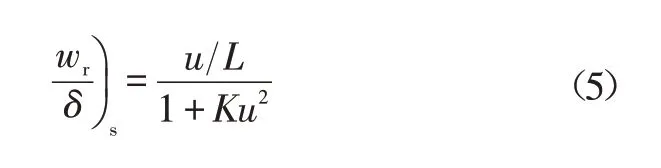
根据K的取值，汽车的稳态响应可分为不足转向、中性转向和过多转向。本文根据实际横摆角速度和理想横摆角速度差值及前轮转角方向判断车辆所处的转向状态，以此进行下一步的稳定性控制器设计。

3 整车稳定性控制器设计

本文采用3层结构设计转向稳定性控制器：上层确定当前时刻施加的横摆力矩，采用滑模控制器，根据二自由度模型得到的当前时刻车辆的理想横摆角速度和理想质心侧偏角，计算出同时跟踪这两个控制变量所需施加的横摆力矩；中层确定施加的附加横摆力矩，采用转向状态预测及模糊控制，基于流挖掘技术及马尔可夫模型的预测算法，预测下一时刻车辆的转向状态，通过模糊控制决策出未来时刻需要的附加横摆力矩；下层为驱动力矩分配器，根据得到的总需求横摆力矩和其他约束条件，分配各车轮所需的驱动力矩。控制系统的具体结构如图2所示。

图2 横摆稳定性控制器结构原理

3.1 基于滑模控制的横摆力矩决策

考虑到车辆的质心侧偏角和横摆角速度是车辆稳定性的重要状态变量，针对分布式驱动电动汽车，运用滑模控制理论，以线性二自由度车辆模型为基础，进行质心侧偏角和横摆角速度联合控制，设计针对当前时刻的横向稳定控制器。二自由度状态空间方程为：

式中，Mz1为从上层控制器施加的等效横摆力矩；

滑模平面定义为：

对s求导可得：

式中，λ为滑模面控制参数。

为了改善趋近运动的动态品质，定义等速趋近律[13]为：

式中，ɛ为系统的运动点趋近于切换面s=0的速率。

为了解决系统中符号函数引起的抖振问题，采用饱和函数对其进行替换：

式中，k为边界层厚度。

由式（6）、式（8）～式（10）得到施加的横摆力矩：

3.2 马尔可夫理论

马尔可夫过程（Markov Process）是一类随机过程，其未来的演变只与当前状态有关，不依赖于过去的状态。马尔可夫过程{Xn,n∈T}的参数集T为离散的时间集合，即T={0,1,2,…}，对任意的正整数n∈T和任意的离散的状态集I={i0,i1,…,in+1}，其条件概率满足：

系统由n时刻的状态i转移到(n+1)时刻状态j的一步转移概率为：

本文基于马尔可夫模型，考虑车辆的转向状态构建转移概率矩阵。

3.3 基于流挖掘技术的转向状态预测

流挖掘技术是1998年数据流概念提出后兴起的，是从快速或连续的数据记录中提取知识的过程[14]。考虑到车辆运行数据流的实时、连续、庞大等特性，流挖掘中概要数据构建技术、滑动窗口技术以及自适应等技术可用于解决车载处理器有限的存储空间和计算能力问题，为整车控制器设计奠定了重要基础[15]。

根据采集的当前行驶工况数据，将计算得到的期望横摆角速度与实际横摆角速度的偏差e和采集的前轮转角δ分类。为了顾及驾驶员的乘坐舒适性，避免产生过大或过小的附加横摆力矩，本文将横摆角速度偏差e分成7组，分别对应大不足转向、中不足转向、小不足转向、中性转向、小过多转向、中过多转向、大过多转向，如表1所示。设定相对应的横摆角速度偏差阀值e1～e6，当下一时刻车辆为中性转向时，控制器将不会开启。设定前轮的左转向为正，每个行驶周期的状态量为Si(i=1,2,…,7)。

表1 转向状态分类

基于流挖掘技术及马尔可夫模型的预测算法预测下一时刻的转向状态，构建的动态转移概率矩阵P(t)为：

式中，pij(t)(i,j=1,2,3,…,7)为t时刻的状态转移概率。

车载处理器每次采集1个新样本，过期的样本自动剔除，保证缓存区的样本数据容量恒定，实时更新状态转移概率矩阵。滑动时间窗口根据预测误差实时调整大小，避免无效数据及外界噪声的干扰，预测值更接近实际值。

前轮转角同样影响车辆的行驶状态，前轮转角预测与转向状态预测过程相同。对前轮转角进行合理分类，本文设定状态量为Zi(i=1,2,…,7)，分别代表负大、负中、负小、零、正小、正中、正大，如表2所示。设定相对应的前轮转向角阀值q1～q8，将前轮转角预测值与对应时刻的转向状态Si实时输入给附加横摆力矩决策层，进行横摆力矩修正。

表2 前轮转向角分类

3.4 基于模糊控制的附加横摆力矩决策

该模糊控制器以未来时刻前轮转角δ'及车辆转向状态S为控制输入，以附加横摆力矩控制律U为输出，定义δ'、S和U的模糊子集为：{NB（负大）,NM（负中）,NS（负小）,ZE（零）,PS（正小）,PM（正中）,PB（正大）}。

模糊控制规则是模糊控制器的核心，它的正确与否直接影响到控制器的性能。当预测到车辆将要进入较大的不足转向或过多转向状态时，控制器提前施加较大的控制量，反之则减小控制量或不干涉，通过模糊输出转换为实际的控制输出，得到附加横摆力矩ΔMz。根据试验结果反复试凑，最终确定的模糊控制规则如表3所示。

3.5 驱动力矩分配

根据上、中层控制器的计算结果，得到总期望横摆力矩Mz=Mz1+ΔMz。下层控制器基于直接横摆力矩控制实现各驱动轮转矩的合理分配，以达到车辆稳定行驶的目的。

表3 模糊控制规则

分布式驱动电动汽车稳定行驶时整车驱动转矩为：

式中，Tt为整车总驱动力矩；T1～T4分别为左前轮、右前轮、左后轮、右后轮的驱动力矩。

考虑到前轮转角很小，δ≈0，假设前、后轮距相等，根据期望横摆力矩进行各车轮驱动转矩的合理分配，满足：

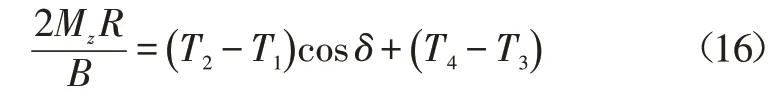
式中，R为车轮半径。

考虑到车辆行驶过程中前、后轴载荷的变化，对前、后轴载荷进行估算：

式中，Fzf、Fzr分别为前、后轴载荷；ax为车辆纵向加速度；hg为整车质心高度。

根据车辆前、后轴载荷对车辆驱动转矩进行分配：

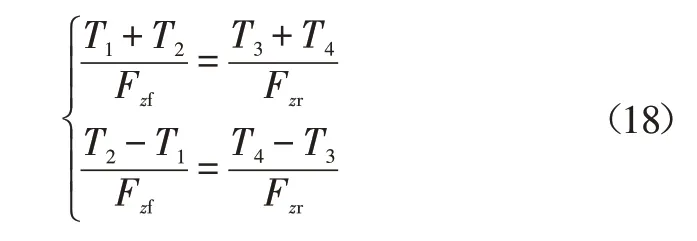
联立式（15）～式（18）可求得各车轮驱动力矩状态空间方程为：

4 仿真分析

基于MATLAB/Simulink构建分层控制器，整车动力学仿真模型由CarSim软件提供，对有、无基于流挖掘转向状态预测的稳定性控制器进行对比分析。双移线工况试验常用于汽车行驶稳定性评价，考虑到驾驶员行为与车辆控制器之间存在一定的时间延迟，本文采用一阶滞后环节在整车仿真模型中模拟执行机构的时间延迟过程：

为验证基于马尔可夫模型及流挖掘技术的转向状态预测算法的准确性，选择双移线工况进行仿真，设置路面附着系数μ为0.75，车速恒定为100 km/h。针对无控制策略的车辆模型，实时采集行驶过程中期望横摆角速度与实际横摆角速度样本数据，通过所提出的预测算法进行未来时刻转向状态预测。本文的采样间隔设定为0.01 s，为了便于在坐标系中显示，避免数据过于密集，每10个采样点取1个值，预测状态与实际状态的对比结果如图3所示。预测值与实际值除在个别时间点有差距外，大部分时刻预测效果比较理想。

图3 转向状态预测

图4所示为在双移线工况下无稳定性控制、传统滑模控制及施加转向状态预测控制3种情况下跟随期望轨迹的能力。由图4可知，在车速设定为100 km/h的极限工况下，基于预测控制与仅有滑模控制（无预测控制）的分布式驱动电动汽车仍能很好地跟随期望行驶轨迹，且与无稳定性控制的车辆相比，更有效避免横向失稳。

图4 双移线行驶轨迹跟随情况

图5所示为在双移线工况下施加转向状态预测控制和传统滑模控制对期望车速的跟随能力。由图5可知，两种控制策略均能使车辆保持期望的行驶速度，但前者的跟随效果更好，车速波动幅度较小，有利于驾驶舒适性及主动安全性。

图5 纵向车速跟随对比

图6、图7所示为施加转向状态预测控制、仅有滑模控制和无稳定性控制策略的分布式驱动电动汽车跟随期望横摆角速度和期望质心侧偏角的对比结果。由图6、图7可知，无稳定性控制时，实际横摆角速度和质心侧偏角均出现滞后现象，存在转向失稳的隐患，且偏离期望值较大。施加预测控制与滑模控制均能达到横向稳定性控制的目的，前者跟随期望横摆角速度和质心侧偏角的效果更好，且有效解决了极限工况下驾驶员反应不及时而引起横向失稳的问题。

图6 横摆角速度对比

图7 质心侧偏角对比

2种控制策略下驱动力分配情况如图8所示，由图8可知，相比于仅有滑模控制，施加转向状态预测的控制器可提前决策出下一时刻的附加横摆力矩需求，从而合理分配各轮驱动力矩，使电机输出转矩变化更加平滑，避免力矩频繁振荡的情况发生，从而提高行驶稳定性及驾驶舒适性。

5 结束语

针对高速工况下紧急转向时，分布式驱动电动汽车产生的横摆角速度滞后于驾驶员的转向操作，导致车辆发生不足转向或过多转向，引起车辆横向失稳的问题，本文提出基于流挖掘技术的转向状态预测控制方法对整车稳定性控制策略进行了优化。基于分层控制方法，根据预测的下一时刻转向状态，提前修正横摆力矩需求，从而合理分配各车轮驱动力矩，避免由于驾驶员反应不及时，导致车辆进入不足转向或过多转向状态，有效提高了车辆行驶稳定性。将流挖掘技术应用于车辆控制器节省存储临时数据的内存空间的同时，有利于实时更新控制策略，对提高横向稳定性效果更明显，为提高整车主动安全性提供了新方法。

图8 2种控制策略下驱动力分配情况