基于改进支持向量回归机的锂离子电池剩余寿命预测＊

王一宣 李泽滔

（贵州大学，贵阳 550025）

主题词：锂离子电池 剩余循环寿命 支持向量回归机 粒子群优化 人工免疫算法 完全学习

1 前言

锂离子电池材料本身的特性、外界环境温度及放电深度等均会对其剩余循环寿命（Remaining Useful Life，RUL）造成影响。为保证其安全可靠运行，减少意外发生，RUL预测成为当前研究的热点问题之一[1]。

目前，国内外针对锂离子电池RUL的预测研究已有较为显著的成果。文献[2]利用支持向量机（Support Vector Machine，SVM）算法建立基于特征参量的RUL回归模型，并利用支持向量回归算法实现了对锂离子电池RUL的预测，但预测速度和精度较低；文献[3]用遗传算法对支持向量回归机（Support Vector Regression Machine，SVR）进行全局寻优，改善其回归能力，但仍存在较大误差；文献[4]通过粒子群优化（Particle Swarm Optimization，PSO）算法对SVR参数进行寻优，与蚁群算法相比，具有更高精度，但传统PSO算法存在易陷入局部最小值的缺点，预测结果不够准确。

为保持粒子种群多样性，文献[5]提出了一种完全学习型粒子群算法以解决全局最优解不够精确的问题，但该算法局部搜索能力较差，文献[6]在搜索过程中根据单个粒子和群体的进化信息动态改变权重和加速度等关键参数，但存在易陷入局部最优值的问题，文献[7]提出一种完全学习型粒子群优化（Complete Learning Particle Swarm Optimization，CLPSO）算法，提高了PSO算法的寻优能力，但局部极值的问题仍未解决。人工免疫系统（Artificial Immune Systems，AIS）通过理解内在分布式本质、自我容忍和分散控制机制，建立计算模型来解决复杂问题[8]，将AIS应用于CLPSO算法中，可使其在较好地保留完全学习型算法多样性的同时，提高预测精度和收敛速度，避免个体极值陷入局部最优[9]。

针对上述问题，本文用AIS-CLPSO算法对SVR的惩罚系数和超参数进行优化，使SVR的某些关键参数获得最优，并建立AIS-CLPSO-SVR预测模型，利用美国国家航空航天局（NASA）PCoE（Prognostic Center of Excellence）锂离子电池充放电数据集进行仿真验证，同时与其他模型进行对比。

2 支持向量回归机算法

支持向量回归机是一种基于VC维（Vapnik-Cher⁃vonenkis Dimension）理论框架，通过结构风险最小化解决小样本、非线性问题的回归算法[3]。即使样本数据较少，也可保证较为准确的预测效果和较强的泛化能力。

对于给定训练数据集G={(x1,y1),…,(xi,yi)}，其中，xi∈Rn为输入特征向量，yi∈R（R为实数集）为输出目标值，n=1,2,…,i，Rn为n维向量空间。SVR的目标是寻找函数g(x)，使g(x)与训练集的偏差小于用户定义的不敏感损失函数ε，同时有较高平坦度，若ε较大，则支持向量数量较少。回归函数g(x)的计算方法为：

式中，w为权重矢量；b为偏差。

通过数据训练，寻找w和b使式（1）结构化风险最小，引入松弛因子ζ、ζ*。依据统计学结构化风险准则，可将线性回归求解问题转化为优化问题的形式：

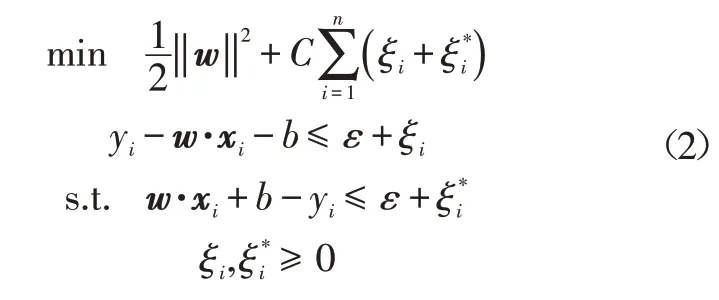
式中，C（C＞0且为常数）为惩罚因子，用于平衡算法复杂度与样本误差之间的权重，对样本中超出误差ε的惩罚度进行控制。

引入拉格朗日函数，SVR模型的回归函数为：

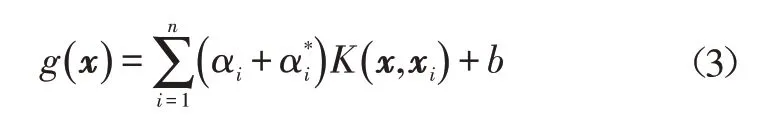
如果σ过小，样本训练准确性一般较高，但泛化能力较差，容易出现过拟合现象；如果σ过大，训练准确性不高。

3 免疫完全学习型粒子群优化算法

3.1 标准粒子群算法

经典粒子群[4]算法依据鸟群觅食行为找到最优解。每个粒子通过全局极值Pg和个体极值Pi自我更新。假设在D维搜索空间中，选取种群中第i个粒子的位置为Xi=(xi1,xi2,…,xid)，其速度为Vi=(vi1,vi2,…,vid)，将每个粒子搜寻到的最优解记为Pbestid，种群搜索到的最优解记为Gbestd。则第i个粒子的位置和速度更新公式为：

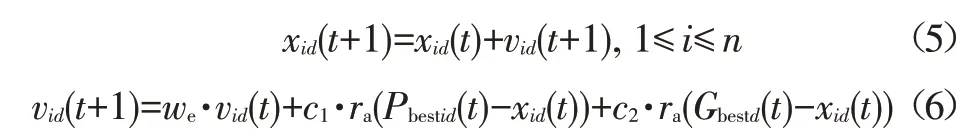
式中，c1、c2为权衡因子；we为惯性权值；ra为介于0和1之间的随机数。

3.2 完全学习型粒子群算法

完全学习型粒子群算法采用新学习策略求解多模态问题[10]。此策略利用任意粒子的历史最优极值Pbest更新粒子速度，更新方程为：

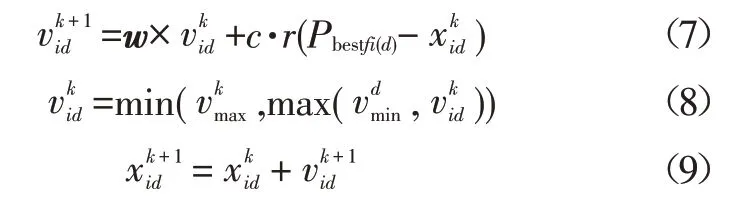
式中，fi=(fi(1),fi(2),…,fi(d))为待选择被学习的第i个粒子样本；Pbestfi(d)为任一粒子Pbest对应的维数。

该决策依赖于学习概率pc，可对不同粒子取不同的学习概率值。在粒子每维中随机生成一个数，将该数与学习概率pci比较，若该数大于pc则学习它本身的Pbest，否则学习其他粒子的Pbest。

基本CLPSO算法通过保证种群差异性，不易使种群陷入早熟收敛并维持了其多样性。但该算法存在一些问题：随机选择的粒子中，选择较好粒子的Pbest进行学习，但若粒子的Pbest未能找到跳出局部最优的有效机制，则种群整体寻优效果会受到影响。

3.3 免疫完全学习型粒子群算法

人工免疫系统通过模拟生物免疫机制形成一种新型仿生优化算法[11]。系统对自然免疫系统的生物学模型进行建模，特别是抗原与抗体的识别和增殖、克隆选择和免疫网络等。其促进高亲和度抗体的同时抑制高浓度抗体，可有效提高算法的搜索效率，加快收敛速度，在具有较高精度的同时维持了抗体群的多样性。

本文将AIS理论应用于完全学习型粒子群算法，结合CLPSO算法和AIS算法的优点，使其在寻优时具有较高精确度。由此建立一种免疫完全学习型粒子群（AIS-CLPSO）计算模型，其流程如图1所示。

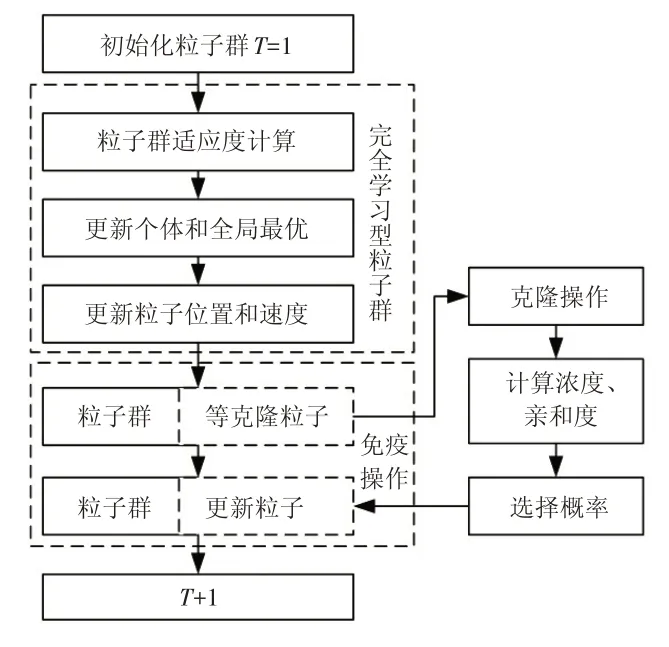
图1 AIS-CLPSO算法流程

由于粒子极值Pbest随着迭代次数的变化而变化，在CLPSO算法中随机运动，算法陷入局部最优时，在参数改变的情况下无法辨识，因此需对CLPSO算法中粒子的Pbest进行免疫克隆选择，提高粒子Pbest全局优化时的效率。

参考文献[12]，相关定义描述如下：

3.3.1 亲和度

亲和度作为权衡抗体抗原间匹配程度的标准，可将其与目标函数M联系起来，亲和度的计算方法为：

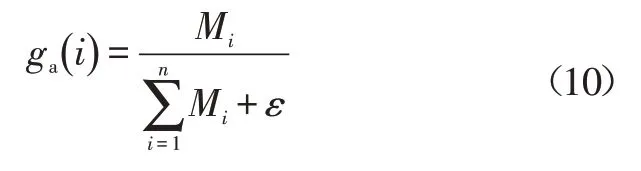
式中，ga为抗体亲和度；ε为非零系数，保证式（10）有意义。

ga越小，抗体亲和度越高，与抗原间的匹配程度越高。

3.3.2 浓度

抗体浓度是种群搜索过程中多样性程度的体现，若某类粒子浓度较高，则抗体多样性较差。将基于距离描述的种群亲和度差值作为表征抗体浓度的方法，可能存在抗体当前浓度很低时具有很大发展潜能的抗体不能被挑选的问题，在一定程度上抑制了种群多样性。因此，本文选择一种用区间描述抗体浓度的方法，取n个抗体，其中每个抗体的亲和度分别为ga1,ga2,…,gan，浓度表达式为：

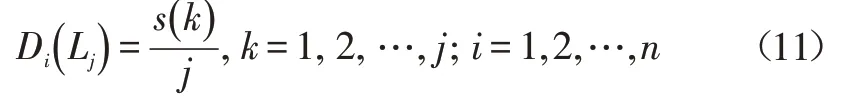
式中，Di(Lj)为每个区间中的抗体浓度，本文将其视为单个抗体浓度；Lj为适应区间进行排序后分成的子区间；s(k)为每个Lj的抗体个数。

由于子区间内部抗体浓度一致，可将具有较大发展潜能的抗体保留，较好地维持了种群多样性。

3.3.3 选择概率

为保持较高的种群多样性，种群通过抑制高浓度低亲和力抗体，促进低浓度高亲和力的抗体来提高种群多样性。基于浓度的选择概率Pd(i)和基于亲和度的选择概率Pa(i)表达式分别为：

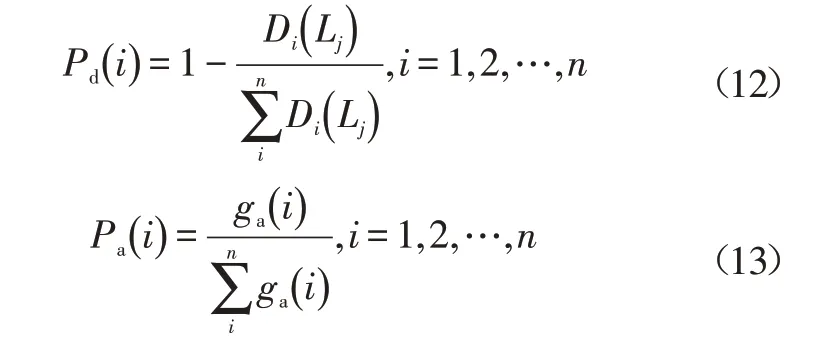
该抗体的综合选择概率为：

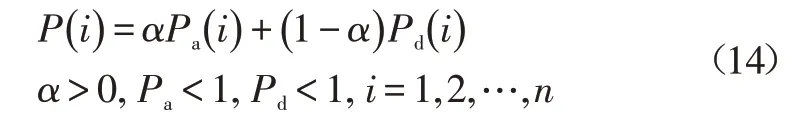
式中，α为协调系数，用于对两种概率进行协调，促进低浓度高亲和度的抗体，从而提高种群多样性。

AIS-CLPSO模型中免疫操作的具体步骤为：

a.挑选数量为m的适应度较高粒子的Pbest，将每个粒子的Pbest构建临时种群，视该种群为AIS中的抗体。亲和度越大，克隆规模N越大，克隆扩增后生成新种群。

b.对新种群中个体进行免疫高频变异：

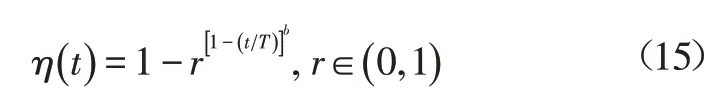
式中，t为种群当前进化代数；b≥0且为常数，一般取b=2。

由式（15）可知，在进化初期变异空间大，而后期在小范围内进行局部搜索。

c.免疫选择操作，选择步骤b变异后亲和度最高的个体进入下一代。

d.通过选择概率函数选取最优抗体，将抗体补充回粒子群。

4 AIS-CLPSO优化SVR模型

为提高SVR性能，本文采用免疫完全学习型粒子群优化算法对SVR算法中惩罚参数C和高斯核函数中参数g进行取值优化，AIS-CLPSO-SVR算法训练结构如图2所示。

具体步骤为：

a.粒子初始化，由SVR的参数C、σ组成一个粒子。

b.通过AIS-CLPSO-SVR算法对参数值进行优化迭代，训练相应的SVR模型，并利用该模型训练和预测样本，达到最大迭代次数或获得满意解时，进入步骤e，否则进入步骤c。

c.粒子个体最优值及全局最优值更新，根据式（5）、式（6）更新粒子速度和位置。

d.本代种群返回步骤b进行判断。

e.保存AIS-CLPSO-SVR算法寻优后的最优参数Cbest和σbest，并使用AIS-CLPSO-SVR模型对数据集进行训练和预测。

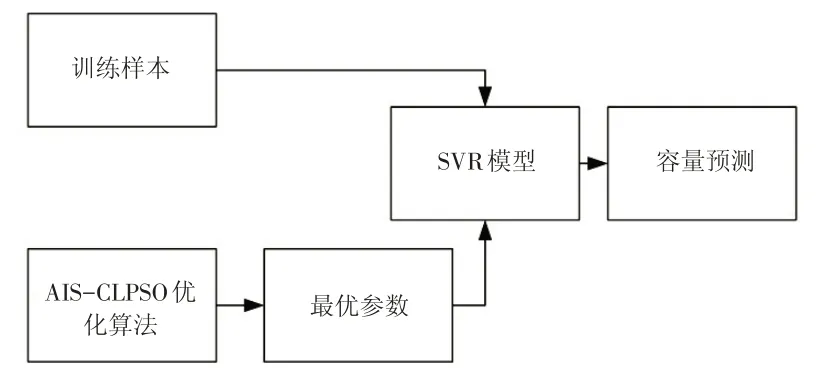
图2 AIS-CLPSO-SVR算法训练结构

5 仿真结果与分析

仿真数据选用NASA PCoE的锂离子电池充放电数据集[13]，本文选取数据集中B5、B6、B18电池试验数据验证模型预测精度，电池额定容量为2 A·h，在室温24 ℃条件下以2 A恒流放电。本文将电池失效阈值设为1.4 A·h，选用电池充放电循环周期作为电池剩余寿命评估标准，B5、B6、B18电池的实际有效循环周期为第124次、第108次和第97次，3种电池容量衰退曲线如图3所示。

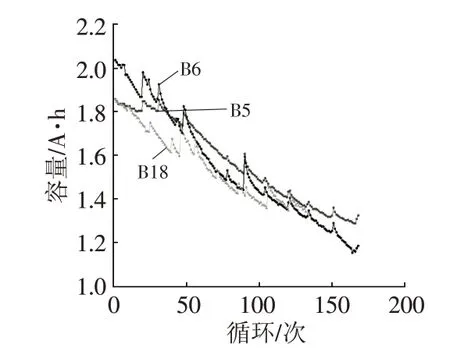
图3 电池实际容量衰退曲线

由图3可以看出，随着锂离子电池充放电次数递增，电池的实际容量呈递减趋势。

为了验证AIS-CLPSO-SVR模型准确性，在充放电数据集B5、B6、B18中选取前45%周期作为训练集，剩余数据为测试集，用于检测和验证。图4～图6为B5、B6和B18电池剩余容量与不同模型预测结果对比。为保证公平，设置AIS-CLPSO和CLPSO中的种群规模为10，迭代次数为100，c1=1.5，c2=1.7。

由图4～图6对比结果可知，AIS-CLPSO-SVR预测模型与电池的实际容量实际误差相差较小。图7所示为B6电池CLPSO-SVR算法预测模型与AIS-CLPSOSVR算法预测模型绝对误差曲线对比。

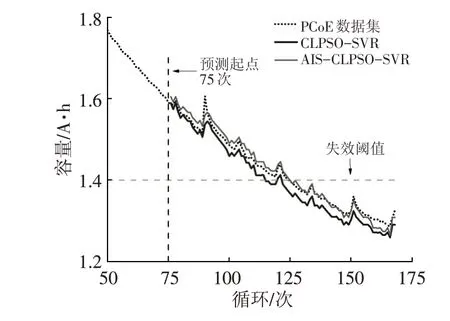
图4 B5电池容量预测结果

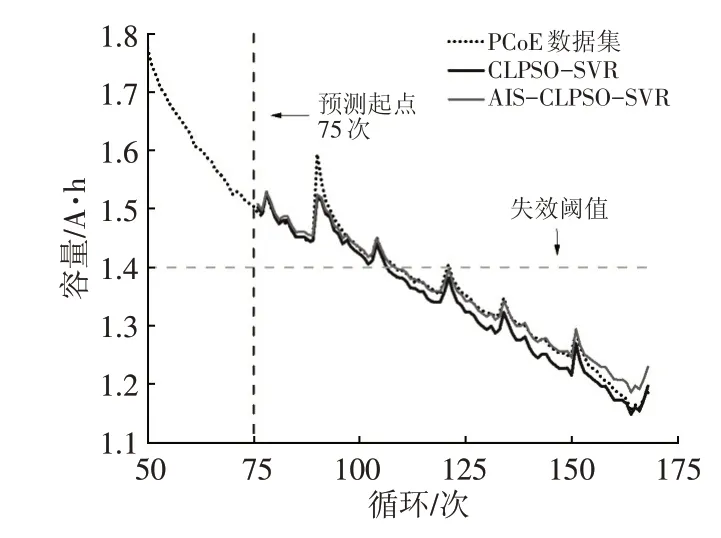
图5 B6电池容量预测结果

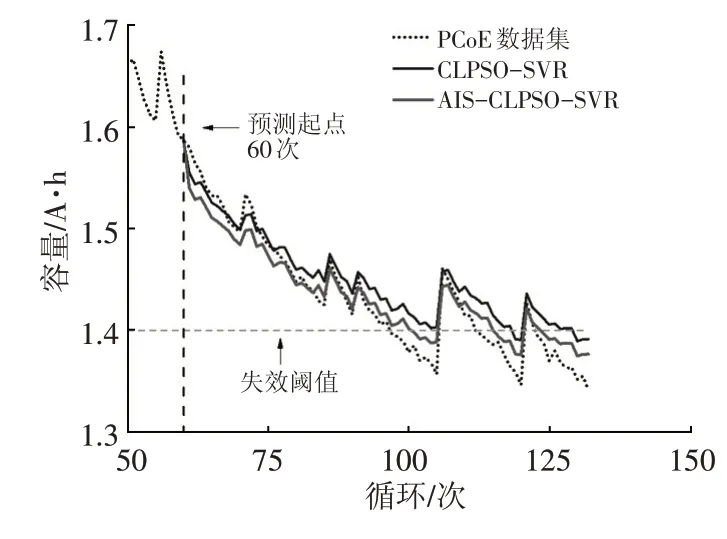
图6 B18电池容量预测结果

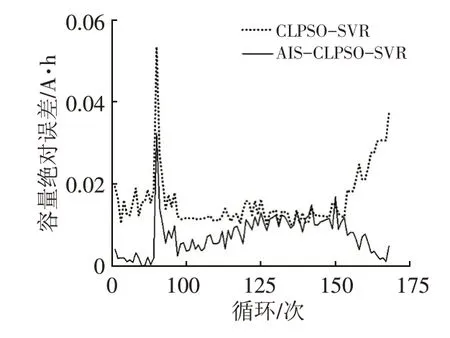
图7 B6电池预测绝对误差曲线

由图7可看出，CLPSO-SVR算法的电池容量绝对误差在0.03～0.05 A·h范围内，AIS-CLPSO-SVR算法的电池容量绝对误差低于0.03 A·h，误差较小。为使对比结果更加清晰，将两种预测模型性能进行对比，结果如表1、表2所示。表1中RUL为电池剩余寿命的真实值，RUL'为电池剩余寿命的预测值，RE为相对误差。

由表1可知，AIS-CLPSO-SVR模型电池剩余寿命预测相对误差低于6%，而CLPSO-SVR模型误差在10%～20%之间，相对误差较大，AIS-CLPSO-SVR模型预测剩余寿命更为准确。

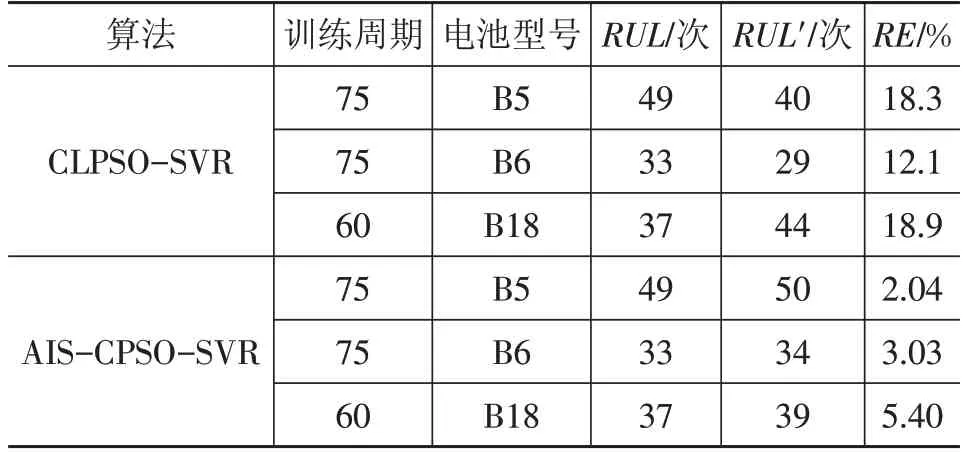
表1 B5、B6、B18电池剩余寿命预测结果对比

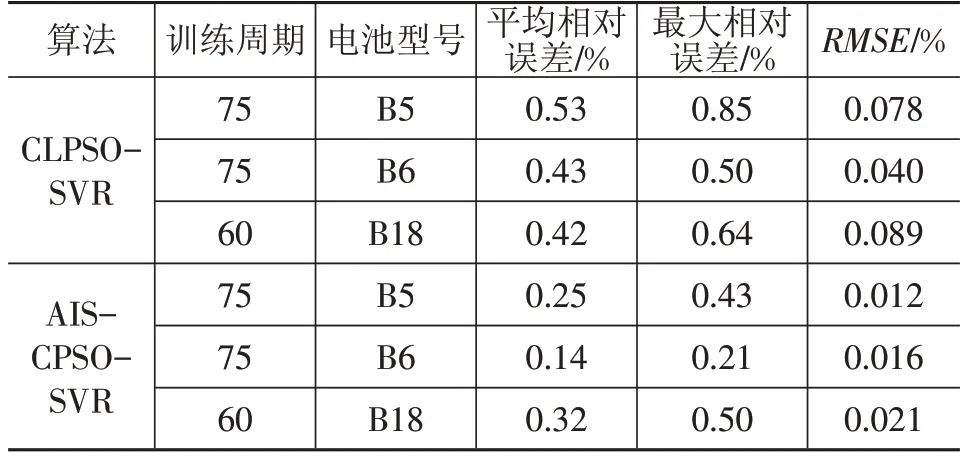
表2 B5、B6、B18电池容量预测误差对比

本文选用均方根误差（Root Mean Squared Error，RMSE）描述两种模型的回归能力：

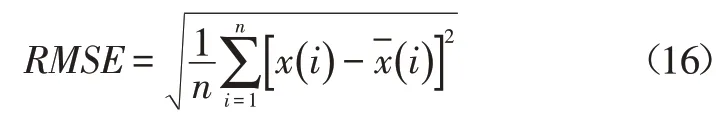
由表2中的容量预测误差可以看出，AIS-CLPSOSVR模型的平均相对误差和最大相对误差均小于CLPSO-SVR模型，且AIS-CLPSO-SVR模型的均方根误差较小。由此可见AIS-CLPSO-SVR模型精度高于CLPSO-SVR模型。

6 结束语

本文提出了一种基于免疫完全学习型粒子群优化SVR的预测方法，用人工免疫算法对CLPSO算法进行优化，改善CLSPO算法易陷入局部最小值的问题，用AIS-CLPSO优化算法对支持向量回归机的关键参数进行优化，建立了AIS-CLPSO-SVR预测模型，最后通过NASA PCoE的锂离子电池充放电数据集将AISCLPSO-SVR模型与CLPSO-SVR模型进行对比，证明了所设计模型具有较强的预测精度。