小学“圆的面积”教学蕴涵的数学学科核心素养

魏闲妹 廖运章

[摘要]以人教版教材六年级上册“圆的面积”为例，结合《普通高中数学课程标准（2017版）》提出的数学学科核心素养的内涵，从生活情境、合情推理、知识可视化三个方面，揭示现实情境视角下“圆的面积”教学中所蕴涵的数学学科核心素养。

[关键词小学数学;圆的面积;数学核心素养;割补转化

[中图分类号]G623.5

[文献标识码]A

[文章编号]1007-9068（2020）32-0029-03

“圆的面积”是义务教育阶段“图形与几何”部分的重要内容，要求学生通过观察、操作、探索等活动，掌握圆的面积公式，并能解决简单的实际问题。“圆的面积”这一课是学生在现实情境下经历从操作验证走向推理论证，实现数学“再创造”的过程，是学生积累数学活动经验和发展数学核心素养的有效课程。

本文将以人教版小学数学教材六年级上册5.3节“圆的面积”为例，结合《普通高中数学课程标准（2017版）》提出的数学学科核心素养的内涵，通过剖析生活情境、可视化圆的面积公式推导等过程，揭示现实情境视角下“圆的面积”教学中所蕴涵的数学学科核心素养。

一、剖析生活情境，发展数学建模素养

数学建模聚焦数学学科核心素养的关键在于：以生活情境为出发点构建数学模型，经历“发现、提出、分析、解决问题”的过程，获得“会用数学眼光看问题、会用数学思维思考问题，会用数学语言表达问题”的能力。

教材中编排的“圆的面积”的内容是简化的数学建模过程。首先，师生通过剖析生活情境中圆坛（草坪）与铺圆坛所需的正方形草皮之间的关系，完成圆的面积概念的建构，进而教师提出问题：“如何计算圆的面积？”其次，学生通过操作、观察、对比等实践活动完成模型的建立：教师引导学生在硬纸上画一个圆，把圆对折分成若干等份后剪开，上下拼接剪开后得到小扇形（如图1），观察后发现拼出的图形是近似的平行四边形（长方形），且随着分的份数越多，拼出的图形越接近长方形。再利用长方形的面积公式，建立圆面积S与半径r之间的函数模型S=π²。最后，通過例1实现模型的应用，即让学生运用函数模型求解下列问题：若圆坛（草坪）的直径为20米，每平方米草皮8元，则铺满草皮需要多少钱？

剖析生活情境的过程中，学生将体验如何通过“数学的眼睛”观察圆坛（草坪），利用“数学的语言”描述和分析圆坛（草坪）的占地面积，最后构建数学问题，即通过建立圆的面积公式这一模型，解决现实生活中与圆的面积有关的具体问题，从而发展学生数学建模素养。

此外，教师可引导学生采用分步法计算例1：第一步，求圆的半径，20÷2=10（米）;第二步，求圆坛（草坪）面积，3.14×10²=314（平方米）;第三步，求铺满草皮所需的金额，314×8=2512（元）。求解的运算程序，可让学生经历探究运算思路、选择运算法则、设计运算程序、求解运算结果的过程，从而发展数学运算素养。

二、借助合情推理，发展逻辑推理素养

逻辑推理素养是依托逻辑推理过程所凝练出来的一种思维品质。圆的面积公式推导可看成逻辑推理的过程，推理的起点是割补转化法和长方形的面积公式，推理的形式是归纳，得到的推理结果是圆的面积等于无限分割后所拼成的长方形的面积。

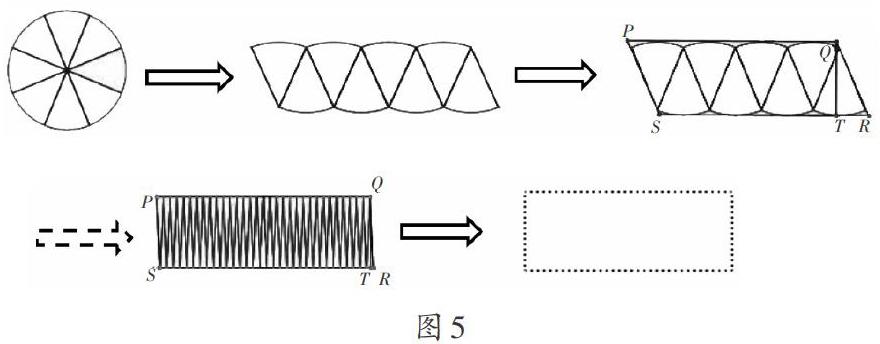
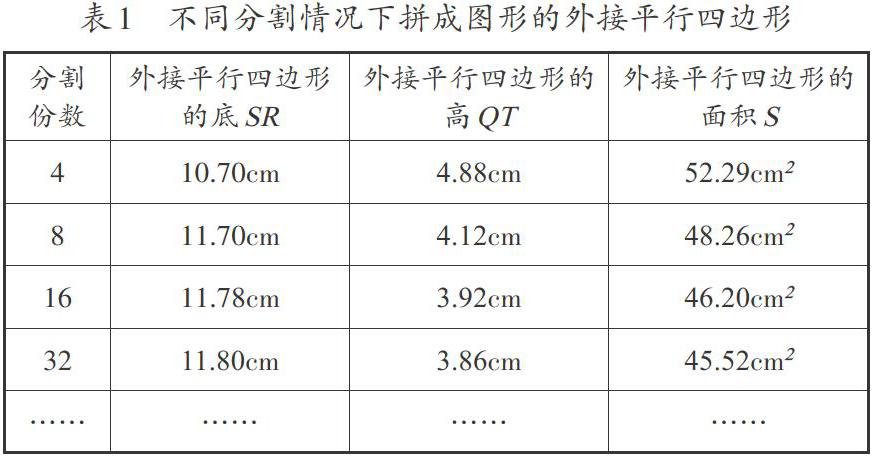
考察分割圆后拼成的图形及其外接平行四边形面积的变化情况。利用几何画板可得到把任意半径（文中取3.78cm）的圆等分成4、8、16、32……4×2^n-1（n≥1）后拼成的图形，以及相应分割下拼成图形的外接平行四边形（如图2）及其底、高和面积之值（见表1）。（此处取π=3.14;记圆的半径为r，外接平行四边形的底为SR、高为QT、面积为S;所有数据只保留小数点后两位）

在用外接平行四边形面积逼近圆面积的过程中，所拼成图形的面积（即圆的面积）始终不变，而用于逼近的外接平行四边形的面积逐渐减小，最后稳定在一个固定的值，即圆的面积。一方面，由图2知，当等分圆的份数越多，外接平行四边形的面积越小，最终与所拼成图形的面积无异。另一方面，随着分割份数的4份、8份、16份、32份，相应地，外接平行四边形的底为10.70cm、11.70cm、11.78cm、11.80cm，最终稳定在11.87cm（≈3.14×3.78）附近，外接平行四边形的高为4.88cm、4.12cm、3.92cm、3.86cm，最终稳定在3.78cm附近，从而外接平行四边形的面积为52.29cm²、48.26cm²、46.20cm²、45.52cm²，最终稳定在44.86cm²（≈3.14×3.78²）附近。

这一过程基于圆的面积不变，从数形结合的角度，使学生理解把圆无限分割后所拼成的长方形（所拼图形的外接平行四边形）的长即圆周长的一半，宽即圆的半径，且长方形的面积即圆的面积。学生经历此过程后，将能对合情推理有大致的了解，形成有条理、有逻辑的思维品质，从而发展逻辑推理素养。

此外，利用几何画板获取半径为3.78cm的圆在不同分割下的外接平行四边形的底、高和面积之值，并将数据整理制成表1，再分析数据得出结论的过程，亦能让学生获得收集、整理数据，并从数据中提取有效信息后做出判断、得出结论的学习经验，从而发展数据分析素养。

三、知识可视化，发展直观想象素养

直观想象素养是空间想象、几何直观和空间观念相互交融基础上价值取向的拓展，是数学活动中探索和形成论证思路、进行数学推理、构建数学结构的思维基础。几何直观将相对复杂、抽象的问题图像化和具体化;空间想象则以现实世界为背景，对事物的几何表象进行加工、改造，甚至创造新的空间想象。几何直观的具体化和空间想象的抽象化使直观想象素养集具体与想象于一体。

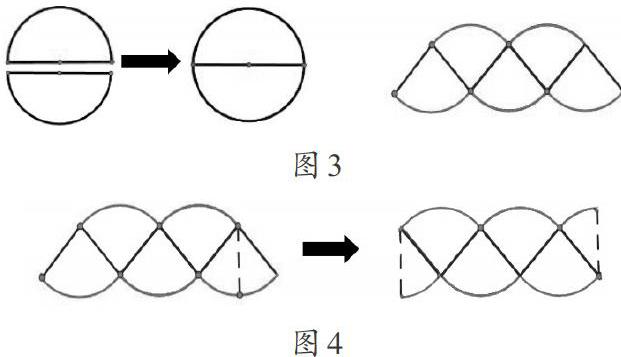
教材编排的“圆的面积”，是通过创设情境，让学生在生活情境中运用直观想象抽离出事物的几何形状——圆，从而将现实问题转化为数学问题。公式推导中，借助几何直观实现分割拼接的过程：先把圆等分成4个相等的小扇形后剪开，再把每个小扇形对折剪开，接着将圆等分成8份，以此类推。其中，等分圆的份数是4的倍数基于以下两个原因：一是将圆等分成两份无操作意义，因为将两个半圆拼接起来还是圆（如图3）;二是小学生的认知能力有限，即此前所学的平行四边形的面积公式推导仅涉及一次割补，因此只考虑将圆割补一次。事实上，若将圆等分成3份，与等分成2份一样无操作意义。若将圆等分成奇数份（如5份），则只需将其中一个小扇形再对折一次后剪开，拼接到两侧（如图4），但此时应使用所拼成图形的外接长方形的面积完成“无限逼近”的过程。

把圆无限分割、拼接、逼近并转化为长方形的过程中，是借助几何直观使复杂的化曲为直过程图像化、具体化，运用空间想象实现逼近、转化的思维抽象过程。一方面，隨着分割份数的增加，外接平行四边形内∠RQT越来越小，斜边QR越接近于高QT，从而外接平行四边形越接近于长方形。若将圆无限分割，则外接平行四边形最终转化为长方形（如图5）。另一方面，随着分割份数的增加，外接平行四边形的面积越来越小，与所拼成图形的面积差也越来越小。若将圆无限分割，则外接平行四边形的面积最终等于所拼成图形的面积（即圆的面积）。

学生经历通过几何图形实现知识可视化的过程，可增强运用几何直观和空间想象思考问题的意识，形成在生活中感悟具体事物本质的数学直观，从而发展直观想象素养。

四、结语

事实上，数学抽象素养的发展贯穿整个教学过程。其中，剖析生活情境是从图形与图形关系中抽象出数学概念（圆的面积）的过程：基于圆坛（草坪）大小，发现这是与圆（空间形式）和大小（数量关系）有关的普遍性规律，从而抽象出圆的面积的概念。公式推导则是从具体事物中抽象出一般规律和结构，并用数学语言进行表征的过程：回顾平行四边形、梯形、三角形的面积公式推导过程，启发学生将圆通过剪拼法转化为近似的平行四边形（长方形）后进行研究（如图1），再基于极限思想，将圆最终转化为长方形，最后观察长方形的长与圆的周长、长方形的宽与圆的半径之间的关系，利用长方形的面积公式抽象出圆的面积与圆的周长、半径之间的一般规律，并用数学公式S=πr²进行表示。

总而言之，现实情境视角下“圆的面积”教学，可让学生经历知识产生以及问题解决的过程，实现学生数学核心素养的发展。同时，数学学科核心素养的发展依托于相应的学习过程，其中，数学抽象是“统领”，数学建模是“大纲”，逻辑推理是“手段”，直观想象、数学运算、数据分析是“工具”，这六个过程相互交融，形成一个有机整体。

（责编 金铃）