问题驱动在学生几何证明学习的实践研究
张碧芬

【摘要】 几何是整个初中数学的重要内容,一直被视为初中教学的重点、难点。它不仅涉及到计算,还需要在解题过程中不断强化学生的逻辑思维,从中寻找切入点。但是这一切入点对于初中生而言,学习比较困难。问题是数学的心脏,以问题驱动引导学生学习,应当成为初中数学教学中的一条基本原则。因此,在初中几何教学中,必须正视初中生几何证明存在的问题,通过分析问题,改善教学,提高教学的质量。本文以初中生《三角形全等的判定定理》的几何证明题为研究视角,对初中生几何证明的学习现状进行了简单的分析,给出自己对几何证明的几点教学建议和教学片断案例,为教师的教学提供一些参考依据。
【关键词】 问题驱动 几何证明 实践
【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711(2020)33-077-02
一、初中生几何证明的学习问题——以《三角形全等的判定定理》为例
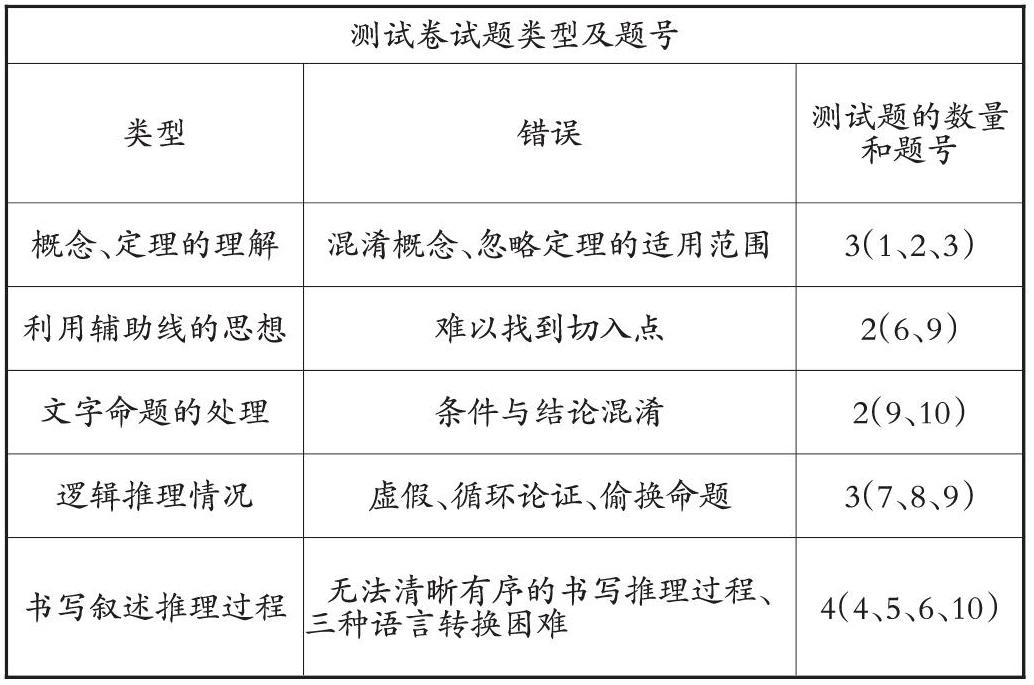
本文通过测试八年级学生在学完《全等三角形的判定定理》后,配合访谈,总结八年级学生在几何证明中存在的学习现状,发现学生在几何证明中的学习问题,参考教材及相关资料编制出测试卷,以本校八年级六个班共265名学生为样本进行测试,根据回收卷的统计结果,对学生存在的问题进行分析。
根据回收卷,学生在几何证明的学习中出现的问题如下表所示:
分析回收卷与访谈结果,总结出初中生在几何证明学习中存在以下的问题:
1. 学生在对几何基础知识的识记和理解不熟练,容易忽略定理的适用范围。
2. 对于需要添加辅助线来完成推理证明的题,找不到连接条件与结论的切入点。
3. 文字命题和实际问题中,对几何图形的抽象存在一定的困难;无法结合题目与图形,找出已知与求证。
4. 几何证明书写时,学生往往出现循环、虚假论证或偷换命题等情况;学生的几何语言比较混乱,主要是表达较为随意,往往出现多余的书写步骤,或漏掉必要的步骤。
二、教学建议及教学片断案例
1. 重视概念,做好基本功练习
在上述回收卷中第1-3题,有20.3%的学生均是对概念的理解不透彻,导致做错。在几何的学习过程中,几何证明中的定理、概念、公式是作为论证推理的依据。对于基础知识和基础概念的教学中,教师应当加强重视。对于基础知识、基础概念的讲解要透彻,教师根据规律和特点,结合已有知识或实际例子帮助学生进行理解,充分发挥教师的主导作用和学生的主体功能。而问题驱动对于新课的导入更能让学生印象深刻。比如,以角的平分线的性质和判定的教学引入为例,可以设计成:
问题1:什么是角的平分线?
问题2:如图,是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放正,沿AC画一条射线AE,AE就是角平分线,你能说出它的道理吗?
问题3:怎么做一个角的角平分线?
问题4:你能说出角平分线所蕴含的数学道理吗?
问题5:若过E点作到角两边的垂线,量一量线段的长度,你能发现什么?
问题6:能否用数学语言总结你发现的数学规律?
通过问题串,学生经历了由回顾旧知,动手将角平分线从理性知识转化为感性知识,最后再转化为理性知识的过程。这样设计不仅吸引学生的注意力,还加深学生对角平分线的概念的理解,强化了学生的作图能力,对于后续角平分线的性质和判定的学习打下了坚实的基础。
2. 注重练习辅助线的基础
在上述回收卷中,有45.2%的学生基本能做出正确的辅助线,但仍有25%的学生对于辅助线毫无头绪。在初中学习中,证明线段或角的关系,多是利用全等三角形或圆的相关知识进行求解。往往需要添加辅助线构造全等三角形或添加辅助线——圆切线进行解决。而利用辅助线主要是帮我们找准题目的切入点,把问题简单化。因此,教师在平时的教学中,应当注重练习辅助线的添加。以下题为例:
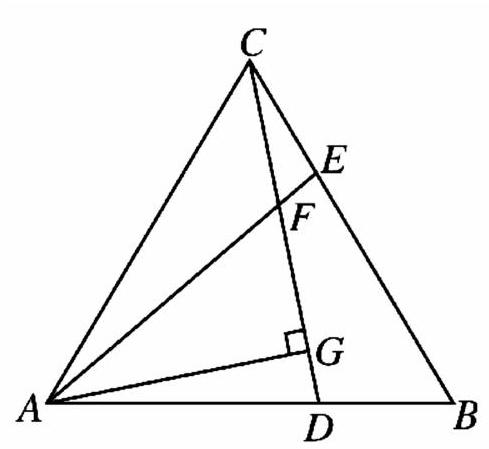
原题是:如图1,已知△ABC是等边三角形。D、E分别是AB、BC上的点,且BD=CE,AE、CD交于點F.求∠BFE的度数。
把本题设计成以下三个问题:如图1,已知△ABC是等边三角形。D、E分别是AB、BC上的点,且BD=CE,AE、CD交于点F.
(1)求证:△ACE≌△CBD
(2)过A作AG⊥CD于G,求证:AF=2FG
(3)如图2,若BF⊥AF,求CF/AF的值。
问题1立足于原题,问题2是通过作点AG⊥CD,利用直角三角形中,30°所对的边等于斜边的一半可以解决问题,问题3在问题1、2的基础上加深难度,也添加了辅助线。一道题可以修改成3个问题串,通过平时练习题一次又一次的辅助线的训练,帮助学生把辅助线的概念深入脑海。基于已有的数学辅助线基础,学生以后遇到相类似的题型,就能进行模仿解决数学几何证明问题。教学中,教师要强调添设辅助线是为了解决问题,所以不能脱离命题的条件和结论去随意添加。在寻找辅助线时,要立足于对题目的分析,进行大胆的尝试。
3.注重逻辑思维能力的培养
在上述回收卷中,发现第8小题有超过35.4%的学生出现逻辑错误,或用不成立的条件得出结论,或用循环使用条件和结论,或把结论和条件颠倒使用,或是把命题更改,进行了错误的论证。结合与学生的访谈,发现学生的逻辑能力较为薄弱,对于逻辑性强的数学学科,这是一个短板。因此,教师在平时的教学中应当注重学生逻辑思维能力的培养。比如,在命题的教学中,可以如此设计:
问题1:“对顶角相等”研究的对象是谁?它具有什么性质?
问题2:什么叫命题?
问题3:什么叫条件?什么叫结论?
问题4:命题当中的条件实质上是什么?命题当中的结论实质上是什么?
問题5:你能用陈述句陈述“对顶角相等”吗?
问题6:如何改写“等腰三角形底角相等”?
学生在一连串的问题下,不仅能确切的掌握住命题的概念,还掌握了把数学结论改写成一般陈述句的数学技能。在掌握命题的概念后,学生的数学逻辑思维能力得到了训练,能确切的识别出条件与结论的关系,对于后续几何证明的书写,奠定了基础。在教学过程中,教师应教会学生使用分析法。即先从结论出发,思考要证明这个结论需要什么条件,而要使这些条件成立的条件又是什么?从结论反推回条件,直至所需要的条件同已知条件吻合,这有利于培养学生的推理能力。
4.明确证明过程的书写要求
在本次测试卷中,除1、2题是客观题,其余均为解答题,1、2、3班有超60%的同学能使表述清楚证明过程,4、5、6班近一半的学生能基本表述清楚。几何语言作为几何的专门性语言,包括了图形、符号和文字语言。使用好几何语言对掌握几何证明题有很大影响。因此,在学习几何时,教师必须明确证明过程中的书写要求。
在学生开始书写几何证明过程时,教师应要求他们每一步都注写依据,使学生清楚知道每个推理都有充分的因果和理由,而且因果关系合理。教师对于例题的板书更需要严谨,学生对于几何语言的使用是通过模仿老师的板书养成的。当学生养成了一定的说理习惯后,才可以适当减少部分标注。如已知条件,已知概念的定义等。在学生掌握基本的推理形式后,各个推理间要有一定的逻辑顺序与联系。在证明过程中,切忌一开始把所有条件全盘托出,缺乏推理之间的逻辑顺序。
学生在书写几何证明过程中,教师要求学生几何字符要对应,要同序。这样不仅可以在学生的潜意识中不断强化对基础知识的理解和记忆;还可以培养学生有根有据讨论问题的习惯;同时,也有利于教师及时发现学生在推理过程中所反馈出来的缺陷。
总之,在几何证明的教学中,应根据学生所反馈出来的问题采取相应的教学措施,而问题驱动始终贯穿在数学教学中。笔者仅从平时的教学中总结教学经验,提出教学建议和教学问题片断案例,供研讨。
[ 参 考 文 献 ]
[1]刘东升.追求适合初中学生的教学深度[J].中学数学月刊.2014(9).
[2]赵艳.问题驱动引出新知,题组变式追求开放[J].教材教法.2018(11).

