异步电动机转子电阻在线辨识和反步速度控制
郭林杰,于海生,吴贺荣
(青岛大学 自动化学院,青岛 266071)
0 引 言
异步电动机因结构简单、造价较低等特点,被广泛应用于工业生产的各个领域[1-2]。由于可以将异步电动机解耦成磁链和转矩两个分系统,达到类似直流电动机的控制效果,故间接磁场定向控制得到了很多学者的关注[3-4]。但间接磁场控制的精确度非常依赖于转子电阻和转子磁链的准确估计[5]。然而,受到温度升高、集肤效应等因素的影响,转子电阻在电机实际运行过程中会发生明显变化,从而影响转子磁链的估计,进一步导致系统控制出现偏差,严重影响间接磁场控制的性能[6]。因而研究转子电阻的在线辨识算法成为矢量控制的热门课题之一。近年来,基于模型参考自适应系统(以下简称MRAS)的转子电阻辨识算法因其结构简单、易于实现的特点而备受瞩目[7]。
文献[8]根据电流型和电压型磁链观测器两者的输出误差,构建MRAS,在线辨识转子电阻。文献[9]设计电磁转矩模型在线补偿转子电阻差值。文献[10-11]采用无功功率模型在线估计转子电阻,并分别利用波波夫超稳定性理论和李雅普诺夫稳定性理论证明了稳定性。文献[12]提出了定子电流与转子磁链点乘的MRAS方案,并进一步分析指出了该方案不受定子电阻变化的影响。
本文在αβ坐标系下推导异步电动机全阶状态观测器,实时估计转子磁链;在此基础上利用波波夫超稳定性理论设计MRAS的转子电阻在线估计算法;最后,设计反步控制器来加快系统响应速度。
1 异步电动机数学模型
异步电动机在αβ坐标系下的数学模型[13]:

(2)
式中:
为电机漏磁系数;isα,isβ分别为定子电流在αβ坐标系下的分量;λrα,λrβ分别为转子磁链在αβ坐标系上的分量;usα,usβ为定子电压分量;Rs,Rr分别是定子和转子电阻;Ls,Lr和Lm分别是定子、转子电感和互感;ωr为转子电角速度。
2 全阶状态观测器设计
在式(1)的基础上建立异步电动机全阶观测器[14]:

(3)
式中:“^”为估计值;G为反馈增益矩阵,用来保证观测器的渐近稳定和快速收敛。
将观测器的极点全部配置到异步电动机极点左侧的k倍位置,以保证观测器的渐近稳定。选择合适的k,使观测器能够快速收敛。
由式(1)可得到异步电动机模型的特征方程:
定义反馈矩阵G:
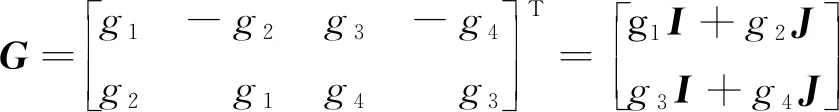
(5)
则由式(3)和式(5)可得出全阶观测器的特征方程:
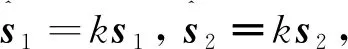
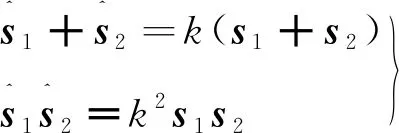
(7)
联立式(4)、式(6)、式(7)可得全阶观测器反馈增益矩阵G的各项表达式:
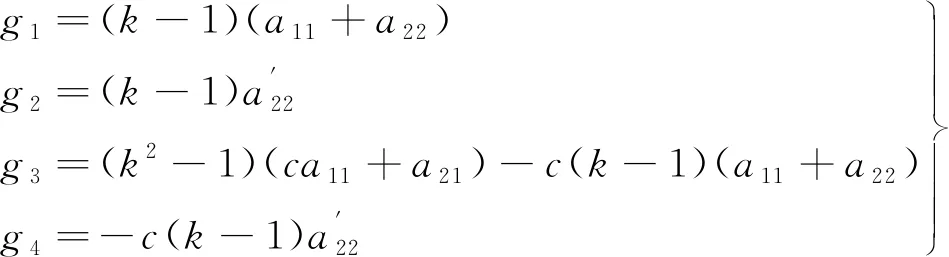
(8)
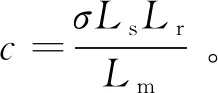
3 转子电阻在线辨识算法
定义观测器状态误差:

(9)
用式(3)减去式(1)得到误差状态方程:
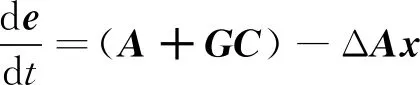
(10)

为了在线估计转子电阻,将异步电动机模型自身作为参考模型,设计的全阶观测器作为可调模型,构建MRAS,全阶观测器中含有待辨识的转子电阻。由于异步电动机转子磁链不能直接测量,选取容易测量的定子电流作为两个模型比较的物理量,并运用波波夫超稳定性理论设计转子电阻的在线辨识算法。
将式(10)代入波波夫不等式[15]有:
(11)
将式(11)进一步整理:
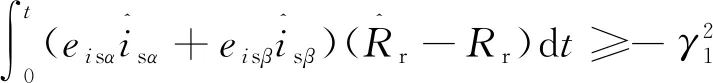
(12)
取转子电阻Rr的自适应律:

(13)
将式(13)代入式(12)可得:

(14)
将式(14)拆解成两部分:
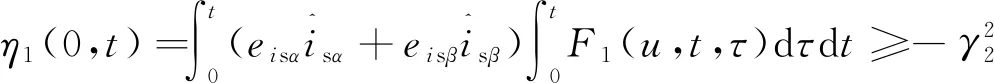
(15)

(16)
若式(15)、式(16)均成立,则可保证式(14)成立。
对式(15)而言,设存在一个函数f(t),其对时间的导数:

(17)
再选取函数F1,使其满足:

(18)
式中:ki为正实数。
将式(17)、式(18)代入式(15)中可得:
由此,式(15)满足不等式。由式(17)、式(18)可得:
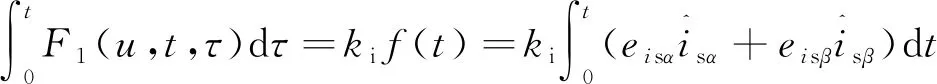
(20)
再对式(16)进行求解,将式(16)整理成:
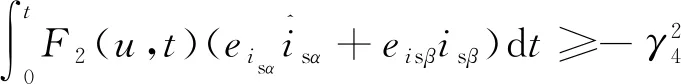
(21)
要使式(21)成立,只需式(22)左边的被积函数为正即可,令:
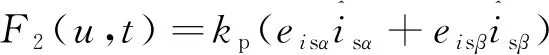
(22)
式中:kp为正实数。将式(22)代入式(21)可得:

(23)
由上式可知,式(18)也满足波波夫不等式。将式(20)和式(22)代入式(13),可得转子电阻自适应律:
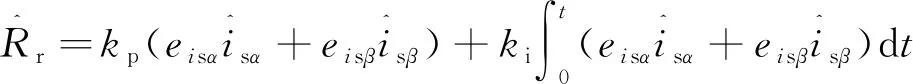
(24)
4 反步控制器设计
定义ω和λrd的跟踪误差:

(25)
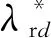
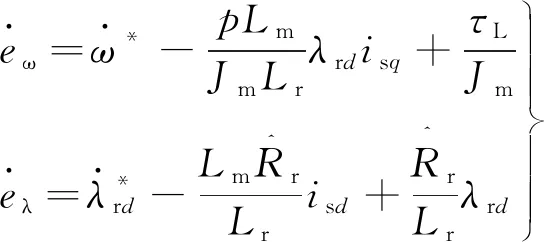
(26)
选择李雅普诺夫函数:
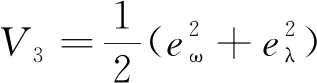
(27)
对上式(27)求导可得:

(28)
为使系统稳定,令:

(29)
此时,式(28)可表示:
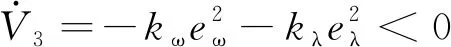
(30)
选取电流isd和isq为虚拟控制量,由式(26)和式(29)可得:

(31)
定义定子电流误差:

(32)
对式(32)求导可得:

(33)
式中:
选择李雅普诺夫函数:
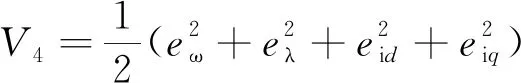
(34)
对式(34)求导可得:
为使控制器渐近稳定,令:
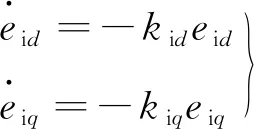
(36)
此时,可以得到控制律:
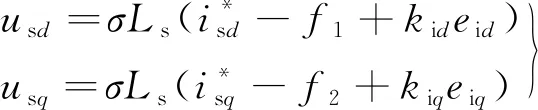
(37)
将式(37)代入式(35)可得:
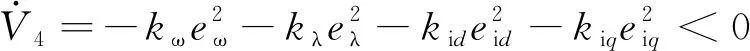
(38)
因此,控制器渐近稳定。
基于转子电阻在线辨识的异步电动机反步法速度控制系统框图如图1所示。

图1 基于全阶观测器的异步电动机 转子电阻辨识和反步控制系统框图
5 仿真结果和分析
利用MATLAB/Simulink平台对本文的控制系统进行仿真实验。异步电动机的参数:额定功率PN=4 kW;额定转速nN=1 400 r/min ;额定频率fn=50 Hz;额定电压Vn=380 V;定子和转子电阻Rs=1.85 Ω,Rr=2.658 Ω;定子和转子电感Ls=0.294 1 H,Lr=0.289 8 H;互感Lm=0.283 8 H;转动惯量Jm=0.128 4 kg·m2;反步控制器中k1=500,k2=200,k3=150,k4=55;极对数p=2;全阶观测器极点倍数k=1.2;辨识系统kp=1.5,ki=300。
异步电动机以60 rad/s的速度空载起动,在t=0.5 s时负载转矩突变为10 N·m,在t=1 s时转子电阻增大50%,变为3.987 Ω。考虑到转子电阻由于温度等因素随时间呈现非线性变化,本文采用指数函数代替阶跃函数来模拟转子电阻非线性变化。选取函数Rr=Rr0+C(1-e-t/T0),C和T0为实常数。由图2可以看出,带有辨识系统的反步控制可以快速跟踪给定转速,当负载转矩发生变化时,转速没有受到影响。由图3可以看出,全阶观测器可以较快地估计出转子磁链的幅值;在转子电阻增大时,无辨识系统的转子磁链幅值发生变化,磁链偏离稳态值1 Wb,有辨识系统的转子磁链幅值没有明显变化。图4中无辨识系统的电磁转矩脉动变大。由图5可以看出,本文的转子电阻辨识算法可以较快、精确地辨识出转子电阻真实值。图6中无辨识系统的转子磁链位置与实际位置不符,这会导致转矩和磁链解耦出现偏差,严重影响系统的控制性能。加入辨识模块后,转子磁链幅值较快回到给定值,转速、转子磁链位置和电磁转矩没有因为电阻变化而产生影响,说明该模块消除了转子电阻变化对间接磁场定向控制的影响。
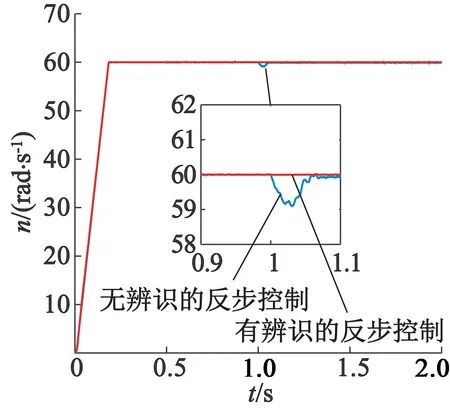
图2 转速变化曲线图
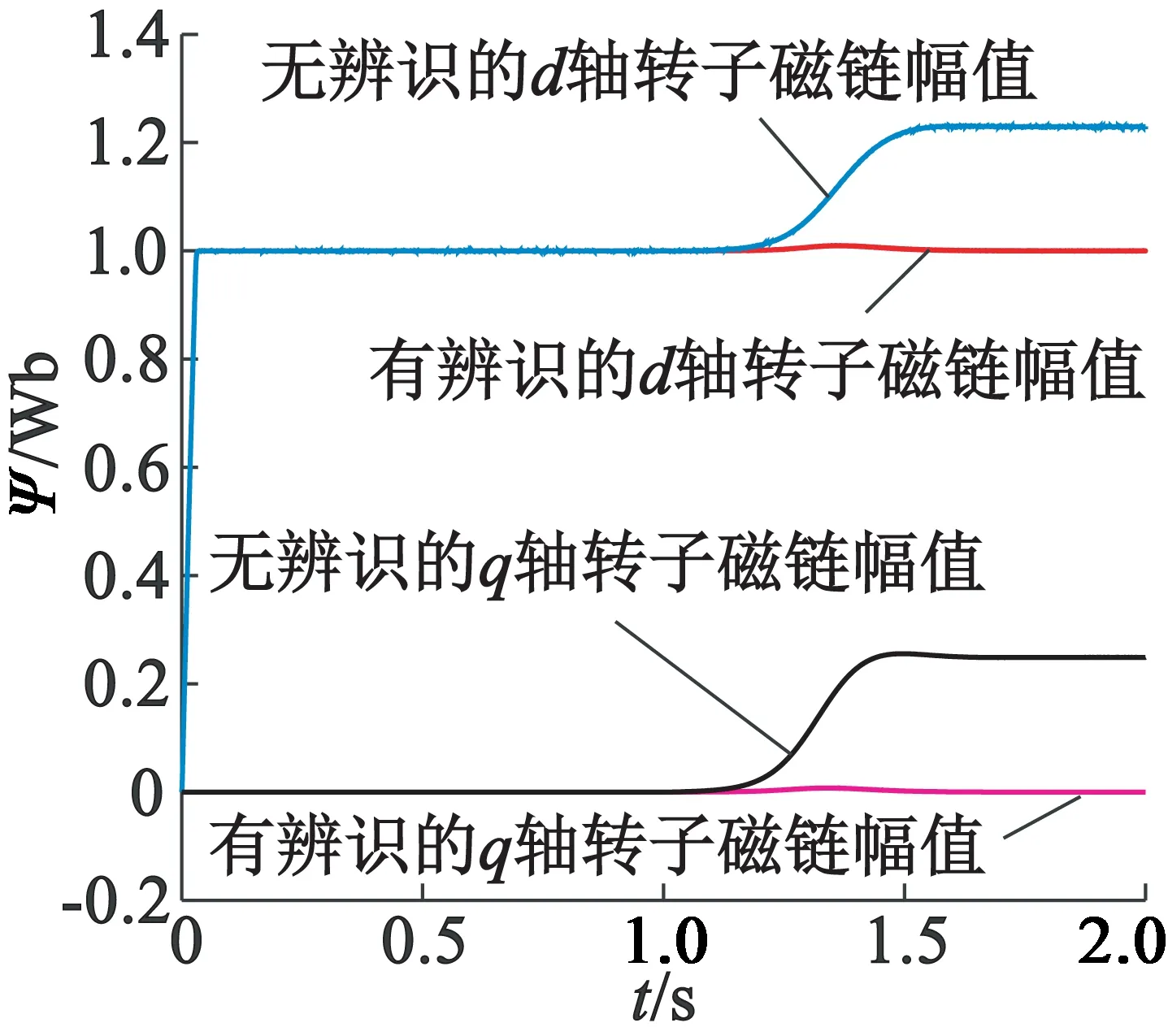
图3 转子磁链幅值图

图4 电磁转矩变化图
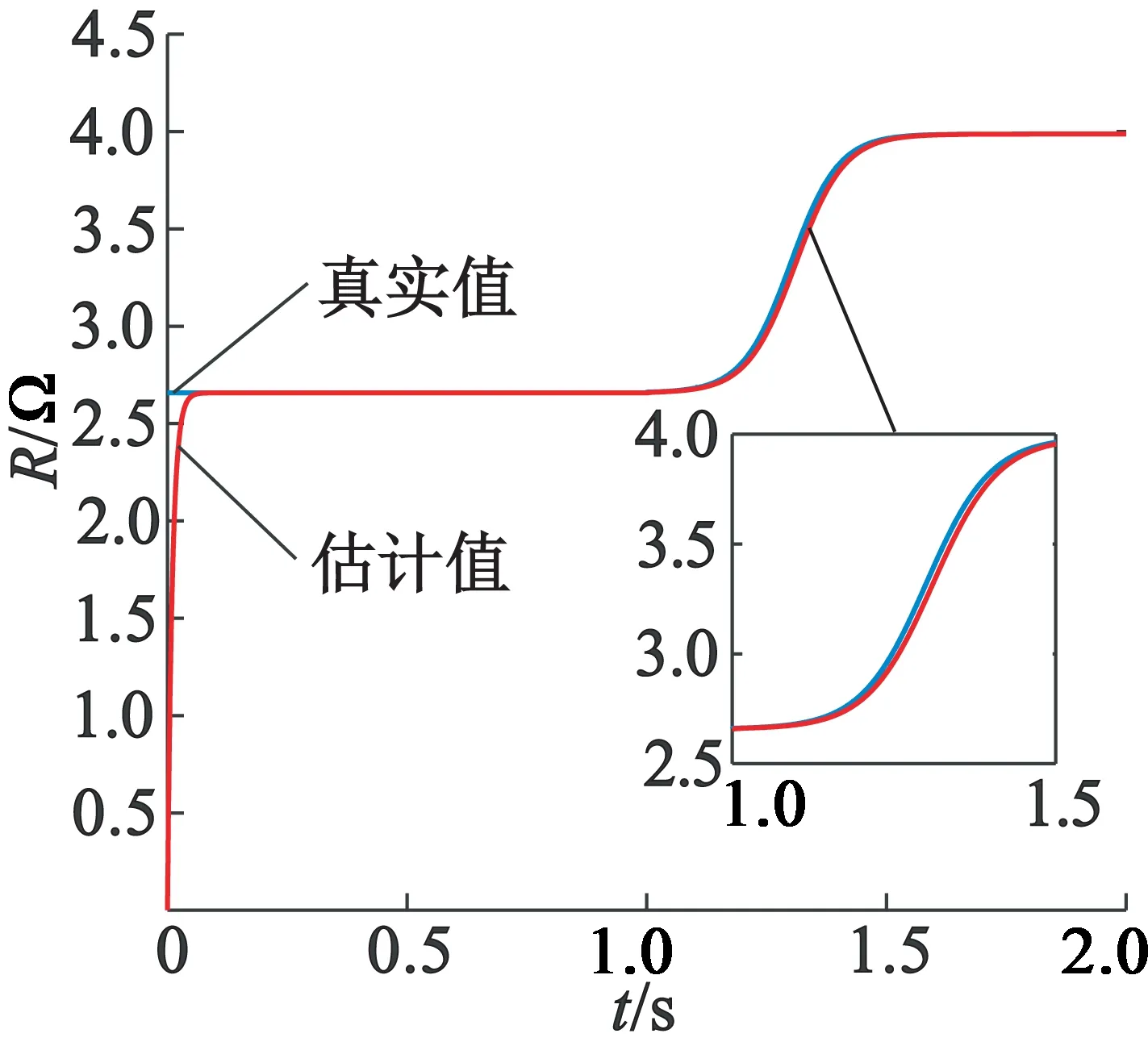
图5 电磁转矩变化图转子电阻估计图

图6 转子磁链位置图
6 结 语
本文对转子电阻辨识问题进行了研究。首先,建立异步电动机全阶观测器,根据极点配置的原则,确定了反馈增益矩阵,以实时观测转子磁链;其次,根据全阶观测器,建立了MRAS在线辨识转子电阻算法,实时更新控制系统中转子电阻的数值;然后,设计了反步控制器,提高了控制系统的控制性能;最后,进行了仿真实验,仿真结果证明了本文算法的正确性。

