兆瓦级直驱永磁同步风力发电机系统研究

林 立，何 洋，周建华，陈鸿蔚

(1.邵阳学院 多电源地区电网运行与控制湖南省重点实验室，邵阳 422000；2.邵阳学院 信息工程学院，邵阳 422000； 3.湘潭电机集团有限公司，湘潭 411100)

0 引 言

海上直驱永磁同步风力发电机(以下简称PMSWG)因清洁、高效、高可靠性，备受各国学者青睐[1]；但兆瓦级电机系统性能要求高、硬件研制与调试成本高，亟待研究如何将电机设计与控制优化有机融合，以提升发电机效率，抑制谐波输出[2]。

近年来，针对电机设计与优化，文献[3-4]通过研究不同工况与功率下永磁发电机的电磁设计及参数对其性能影响，得出铁心长度、极弧系数、气隙长度与永磁体厚度对发电机齿槽转矩及其谐波、损耗与电磁转矩的影响规律。文献[5-10]基于结构与尺寸参数对电机效率与转矩、齿槽转矩及其谐波性能影响规律，利用单变量、多目标耦合寻优得到使发电机性能最佳的气隙长度、永磁体厚度与极弧系数、斜槽宽度与斜极结构；但其性能受结构和大量尺寸参量耦合影响[11]。针对该问题，本文基于电机相似性及其性能分析，提出利用多变量、多目标耦合研究斜极/斜槽结构的360 kW/690 V,200 r/min永磁同步发电机的尺寸参量优化，以提升发电机效率与转矩，削弱齿槽转矩与谐波。

针对电机高性能控制，文献[12]基于永磁发电机线性模型研究了机侧系统双闭环PI控制结构及其参数整定；但PI控制模型依赖性较强[13]，兆瓦级风电调试成本高、研制周期长。针对该问题，本文提出利用有限元法精确建立电机模型，利用场路耦合仿真模拟发电机在四种不同风速扰动、电磁耦合影响参数摄动共同作用下的动态起动过程，验证了系统实现最大功率追踪的可行性。

1 发电机优化设计与分析

1.1发电机尺寸参数优化

依据国家标准，高效、大转矩，谐波畸变与齿槽转矩小是决定PMSWG在全风速实现最大功率追踪与柔性并网关键指标[14]。

电枢斜槽时，其齿槽转矩[11]：

式中：La为铁心长度；μ0为真空磁导率；Di1,D2为定子内径与转子外径；θs0,θs1为定子槽宽与槽距的弧度值；δ为气隙长度；hm为永磁体厚度；Br为永磁材料剩磁；p1为极对数；z为定子槽数；n为使nz/(2p)为整数的最小整数；αp为极弧系数；Nz为斜槽宽度。

电机损耗p与电磁转矩Te[11]:

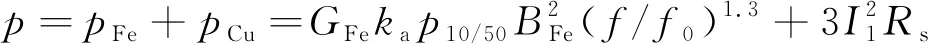
(2)

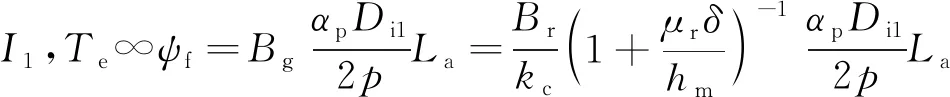
(3)

式中：pFe,pCu为铁耗与铜耗；GFe为铁心重量；ka为铁耗经验系数；p10/50为电磁材料比损耗；BFe为铁心磁密；f,f0为发电机定子交流频率与交流电频率；I1为定子电流；Rs为相电阻；ψf为转子磁链；Bg为气隙磁密；kc为气隙系数。

由式(1)～式(3)可见，发电机效率、转矩受铁心长度、极弧系数、气隙长度、永磁体厚度、斜槽宽度等参数耦合的影响。因此可选铁心长度、极弧系数、气隙长度、永磁体厚度、斜槽宽度为优化变量，发电机的高效、大转矩、齿槽转矩与谐波畸变THD小为约束条件，研究参数对发电机性能影响，利用多变量、多目标耦合寻优，获得使发电机性能最佳的尺寸参数。

1.1.1 铁心长度对电机性能的影响

如表1所示，可由电机的几何相似确定主要尺寸参数，由RMxprt设计永磁同步发电机，添加铁心长度La=0.7～1.3 m优化方案，可得铁心长度对电机齿槽转矩与齿谐波、额定转矩与损耗影响，如图1、图2所示。齿槽转矩与铁心长度成正比，适当增加铁心长度可减少损耗，但有效转矩削弱，且La=0.9 m时，损耗最小。

表1 360 kW/690 V，200 r/min PMSWG主要参数

图1 Tcog,Th与La关系曲线

图2 Te,p与La关系曲线

1.1.2 极弧系数对电机性能的影响

由表1确定主要尺寸参数，并由上文确定最优的铁心长度为0.9 m，由RMxprt设计永磁同步发电机，添加极弧系数αp=0.7～0.8优化方案，可得极弧系数对电机齿槽转矩与齿谐波、电磁转矩与效率的影响，如图3、图4所示。极弧系数与电磁转矩、损耗成正比，与齿谐波成反比，且当αp=0.715，损耗最小；当αp=0.785，齿槽转矩与齿谐波最小。

图3 Tcog,Th与αp关系曲线

图4 Te,p与αp关系曲线

1.1.3 气隙长度对电机性能的影响

由表1确定主要尺寸参数，并由上文确定最优的铁心长度为0.9 m与极弧系数为0.785，由RMxprt设计永磁同步发电机，添加气隙长度δ=1～9 mm优化方案，可得气隙长度对电机齿槽转矩与齿谐波、电磁转矩与效率影响，如图5、图6所示。气隙长度与齿谐波成反比，适当增加气隙长度可增加电磁转矩，减少电机损耗，δ为9 mm或1 mm时，Tcog，Te与p基本一致，但齿谐波最小。

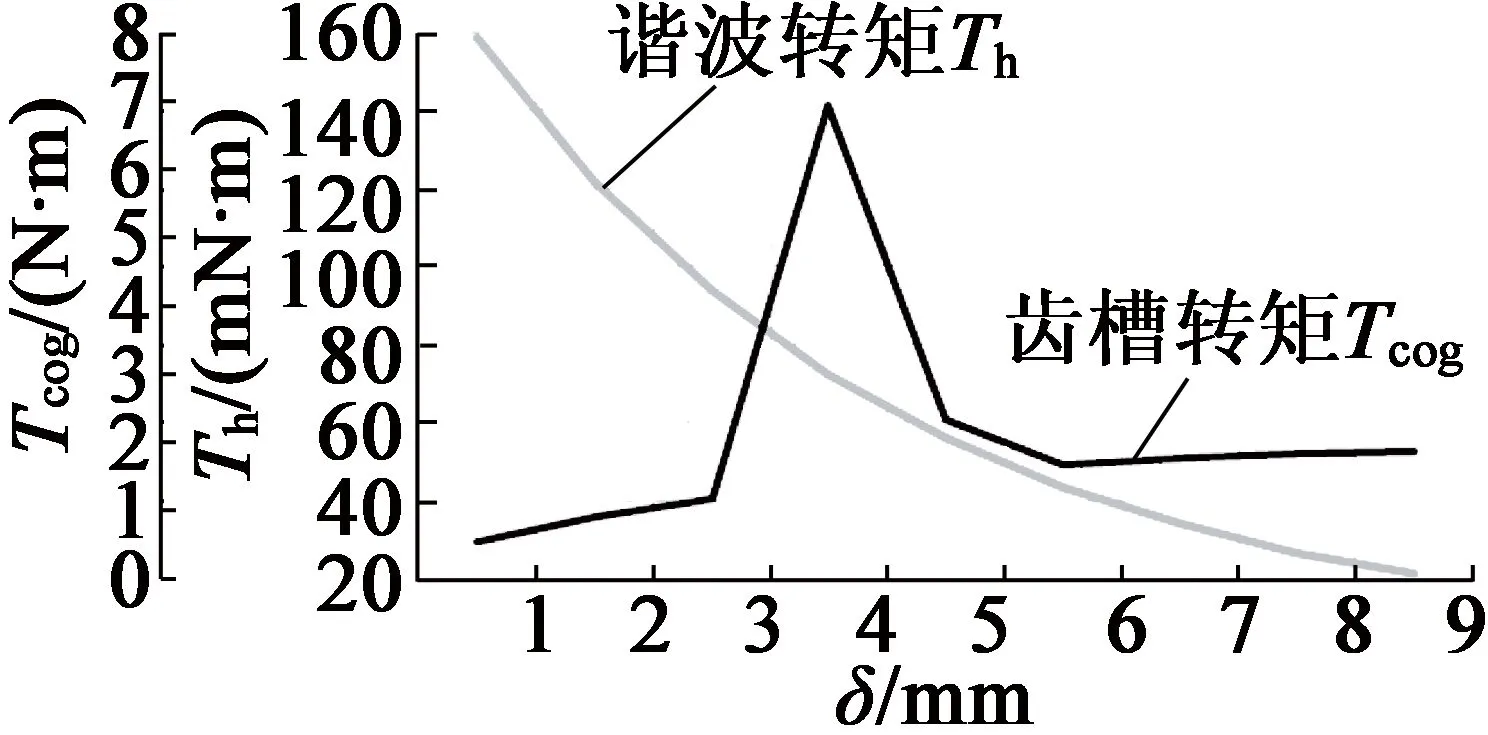
图5 Tcog,Th与δ关系曲线

图6 Te, p与δ关系曲线

1.1.4 永磁体厚度对电机性能的影响

由表1确定主要尺寸参数，并由上文确定最优的铁心长度、极弧系数与气隙长度分别为0.9 m，0.785与9 mm，由RMxprt设计永磁同步发电机，添加永磁体厚度hm=1～9 mm优化方案，永磁体厚度对电机齿槽转矩与齿谐波、电磁转矩与效率影响如图7、图8所示。永磁体厚度与齿谐波成反比，适当增加永磁体厚度可增加Te，hm为9 mm或1 mm时，Tcog基本一致，虽p增加，但Te最大，齿谐波最少。

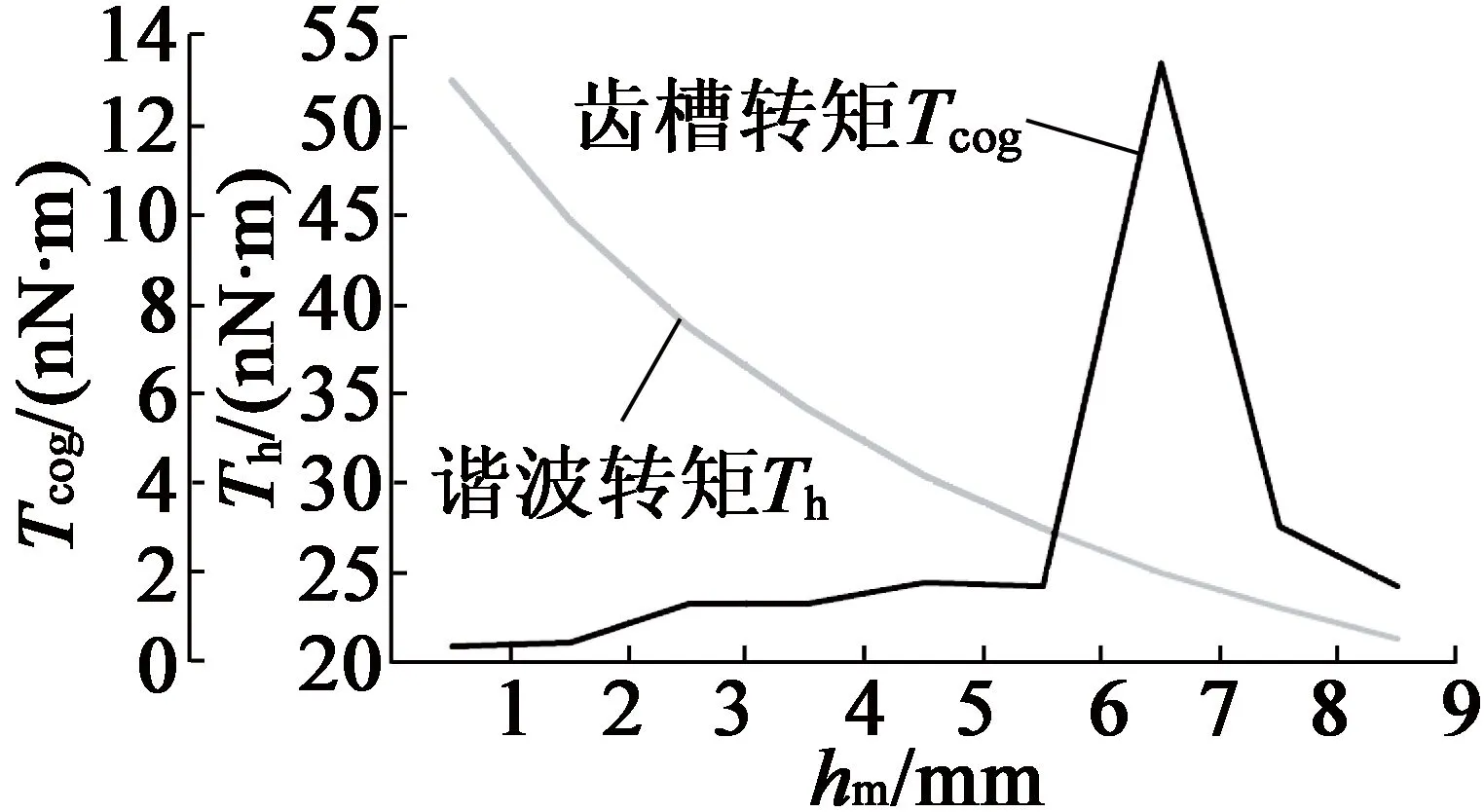
图7 Tcog,Th与hm关系曲线

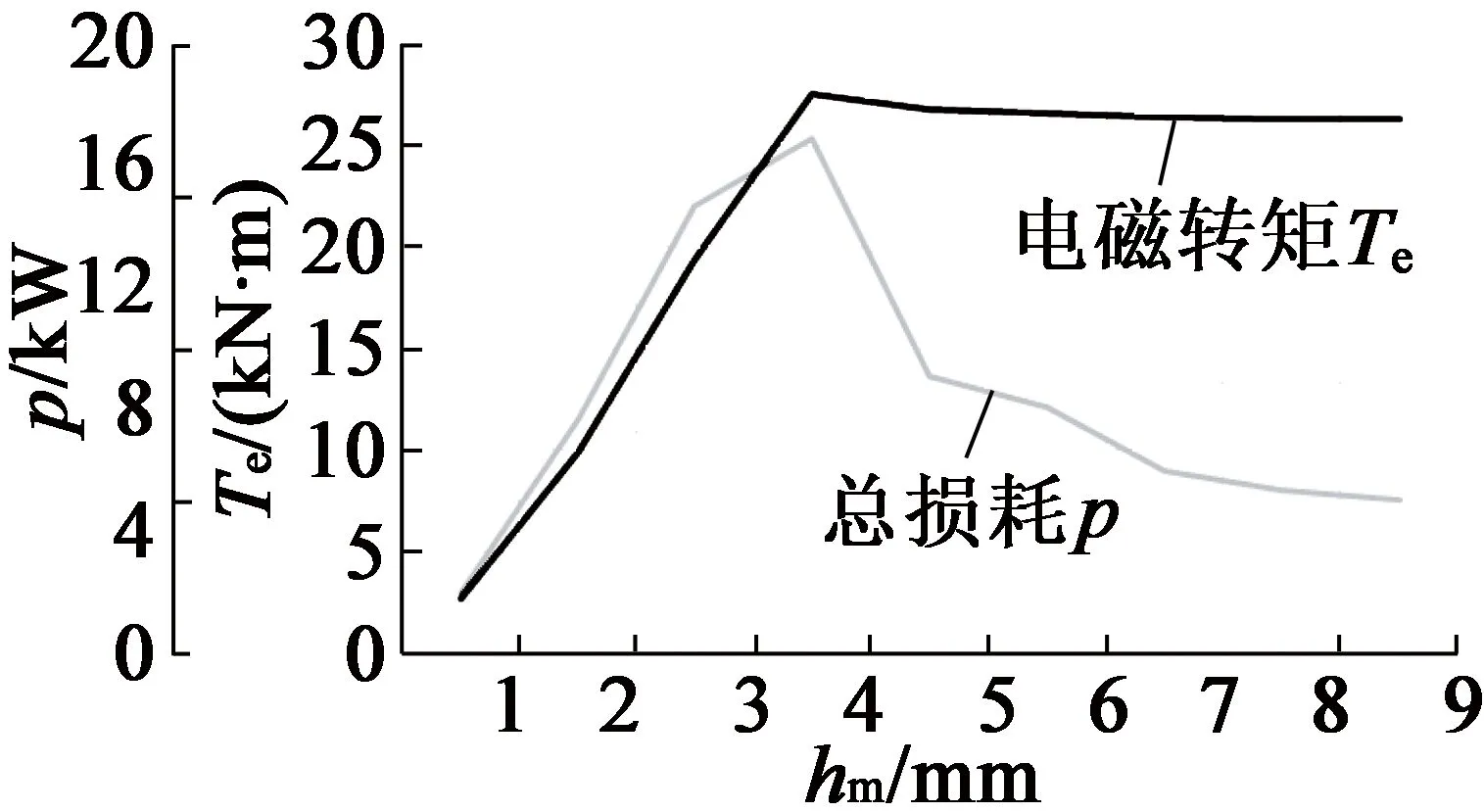
图8 Te, p与hm关系曲线

1.1.5 定子斜槽对电机性能的影响

由表1确定主要尺寸参数，并由上文确定最优的铁心长度、极弧系数、气隙长度与永磁体厚度分别为0.9 m，0.785，9 mm与9 mm，在RMxprt中设计永磁同步发电机，添加斜槽宽度Nz=0～1.0 mm优化方案，可得斜槽宽度对电机齿槽转矩与齿谐波、电磁转矩与效率影响，如图9、图10所示。定子斜槽宽度与电磁转矩和损耗成正比，与齿谐波成反比，适当增加斜槽宽度会削弱齿槽转矩，宽度为1.0 mm时，Tcog≈0，齿谐波最少，Te最大。

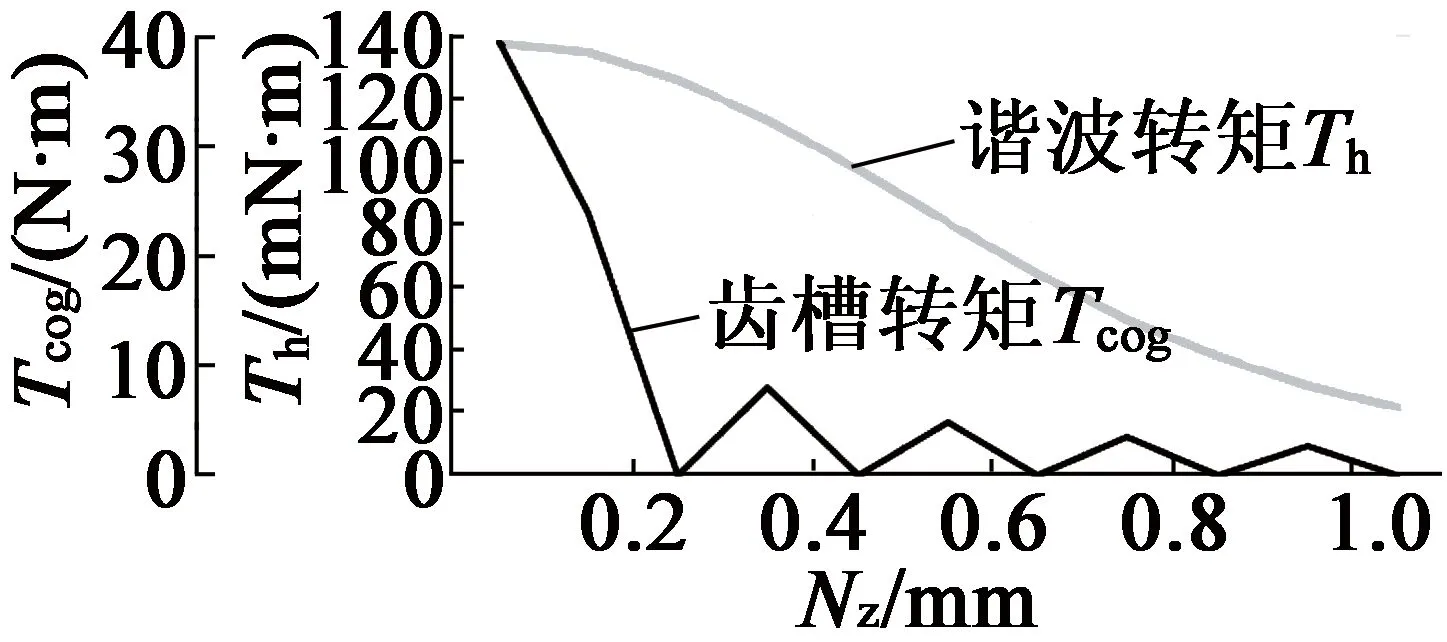
图9 Tcog,Th与Nz关系曲线

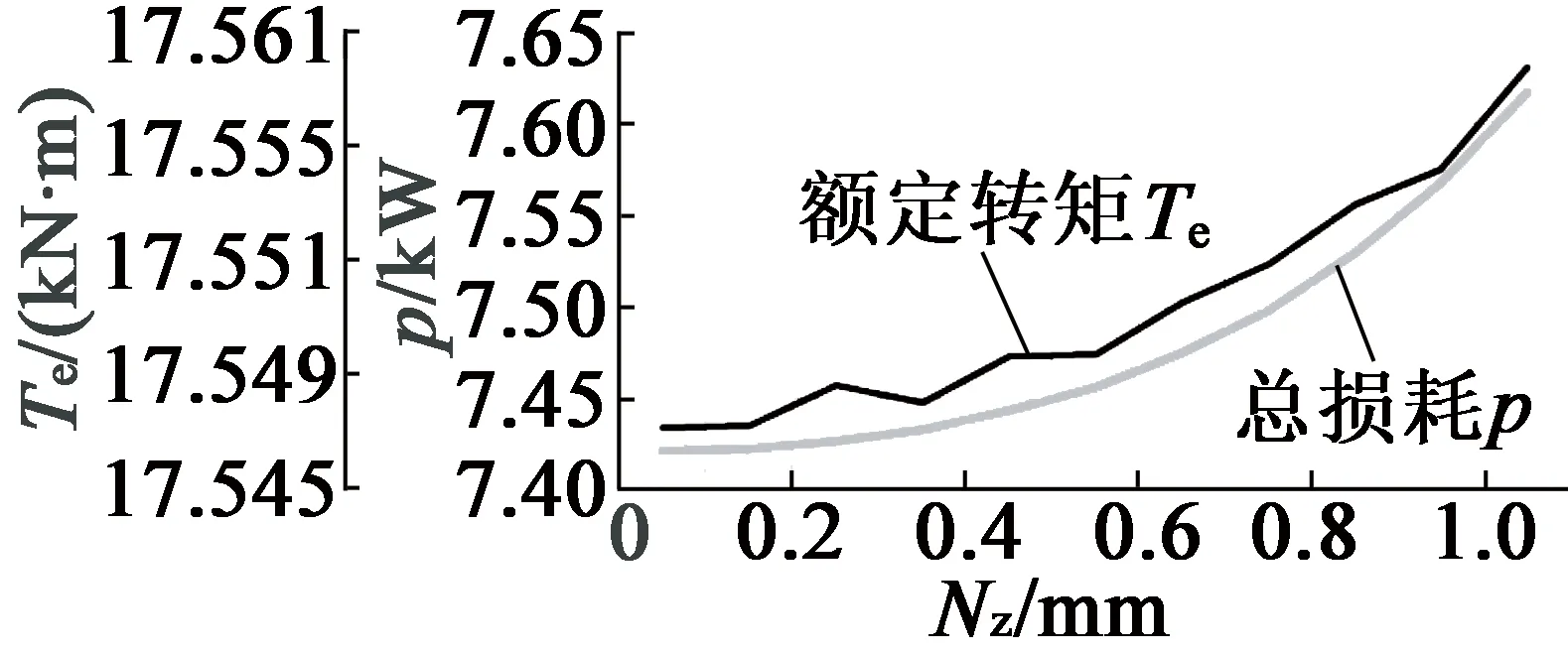
图10 Te, p与Nz关系曲线

1.2发电机优化设计与参数计算

由上述电机性能分析，利用多变量、多目标耦合寻优设计永磁发电机结构及尺寸参数如表2所示。定、转子采用梨形斜槽与双向斜极，尺寸参数与绕组接线如图11所示。

表2 360 kW/690 V，200 r/min PMSWG优化后参数

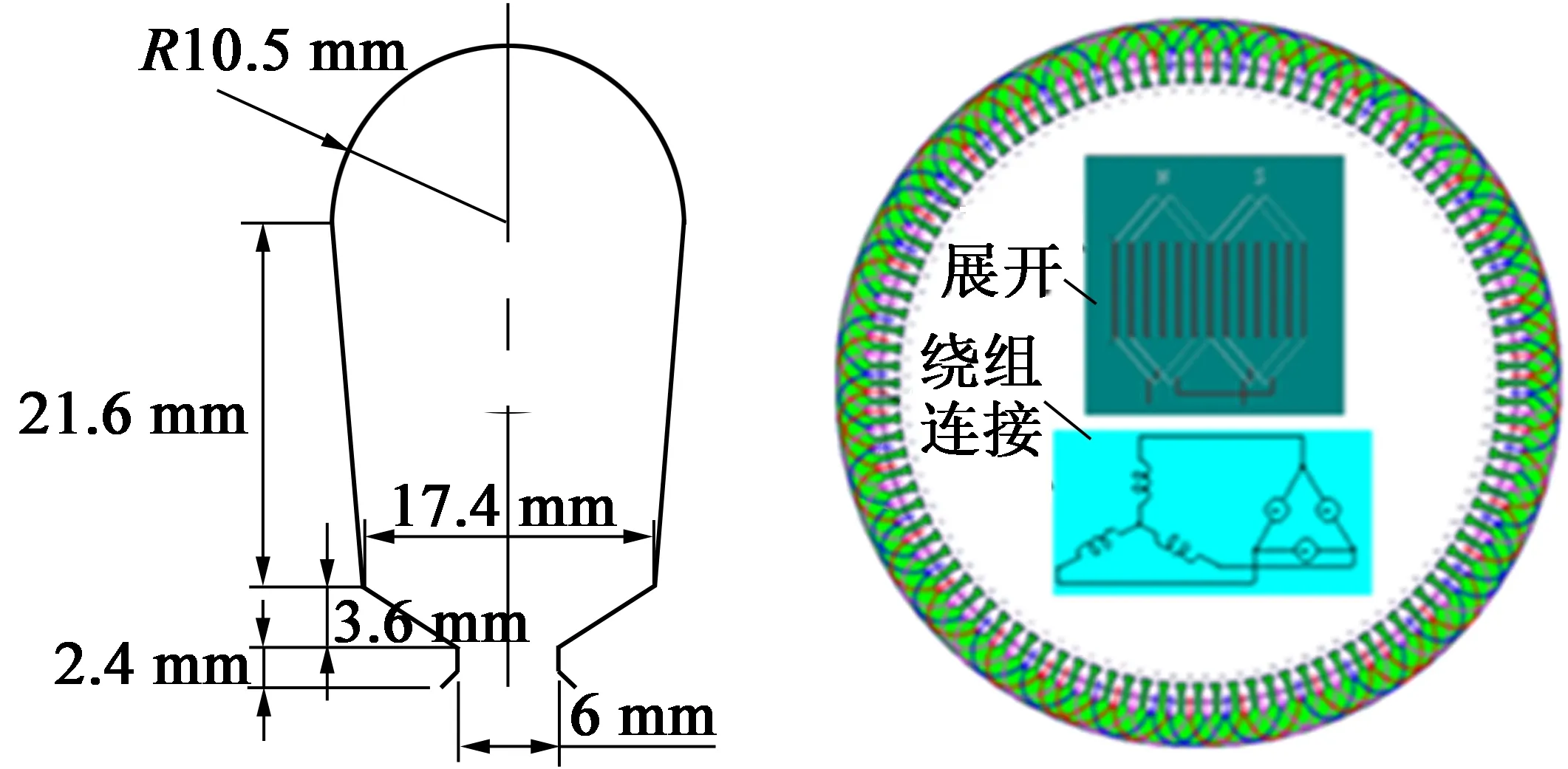
图11 槽形尺寸与绕组接线方式

因风速变化引起该发电机转速波动仅0.6 r/s，由似稳电路定义得电机运行在稳态。

经RMxprt设计，电机端部漏感Lσ[15]：

(4)

式中：N1为每相线圈匝数；Kdp1为绕组系数；d为线圈直线部分伸出铁心的长度；fd为线圈端部轴向投影长度；p1为极对数。经计算，Lσ=12.6 μH。

稳态下电阻Rs[11]：

(5)

式中：ρCu为铜的电阻率；Lav为线圈半匝长度；ACu为导体截面面积。计算得到Rs=0.21 Ω。

稳态下d，q轴电感Ld,Lq[15]：

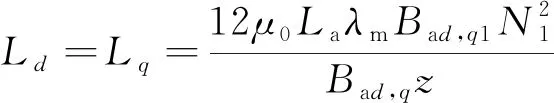
(6)

式中：Bad,q1,Bad,q为d，q轴电枢磁场的基波磁密幅值与磁密最大值；λm为相对磁导率。计算得到Ld=Lq=0.63 mH。

电机的空载总磁通[11]：

ψf=2πD2BgαpLa

(7)

计算得到ψf=1.15 Wb。

2 发电机主电路与控制建模

2.1直驱永磁风电机组的数学模型

2.1.1 风力机

由Betz理论，风力机输出轴上机械转矩Tm、捕获风能能量系数CP[16]:

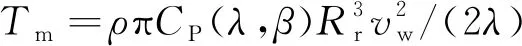
(8)

式中：ρ为空气密度；λ为叶尖速比；β为桨距角；Rr为叶轮半径；vw为风速。

由叶尖速比定义可得不同风速下发电机的最佳电角速度[16]：

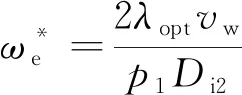
(10)

式中：λopt为式(9)极值对应最优λ值。

2.1.2 永磁同步发电机

经坐标变换，转子磁链定位在d轴，则dq坐标系下永磁同步发电机数学模型[17]：

(11)

(12)

Te=3p1[ψf+(Ld-Lq)id]iq/2

(13)

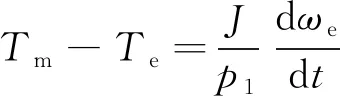
(14)

2.2发电机侧系统结构与等效电路

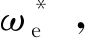
图12 PMSWG侧系统的结构

3 场路耦合仿真及分析

3.1发电机主电路与控制仿真

3.1.1 风力机

由上述分析可建立风力机仿真模型,如图13所示。包括能量系数与转矩模型(式(8)、式(9))、轴转速与叶尖速比求解(式(10))。

3.1.2 主电路与控制仿真

电机设计后，由Maxwell有限元法建立电机模型，计算得电机的转动惯量为489.449 kg·m2；由直驱永磁发电机侧系统结构与等效电路，可在Simplorer下搭建主电路与控制仿真模型。由RMxprt计算，为安全考虑,选择1 200 V/995 A IGBT作为整流电路；控制模型由转速环PI,dq轴电流环PI，dq轴电压前馈补偿，坐标变换与电压空间矢量变换模块组成。

3.2仿真环境设置

为验证360 kW/690 V，200 r/min直驱永磁风电机组在四种不同风速，采用双闭环PI控制实现最大功率追踪的可行性，构造由0～1 s基本风、1～3 s阵风、3～4 s渐变风、4～6 s随机风组成的分段风速模型,如图14，基于电机设计所构建精确模型，采用表3控制器参数进行仿真，步长为1 ms。

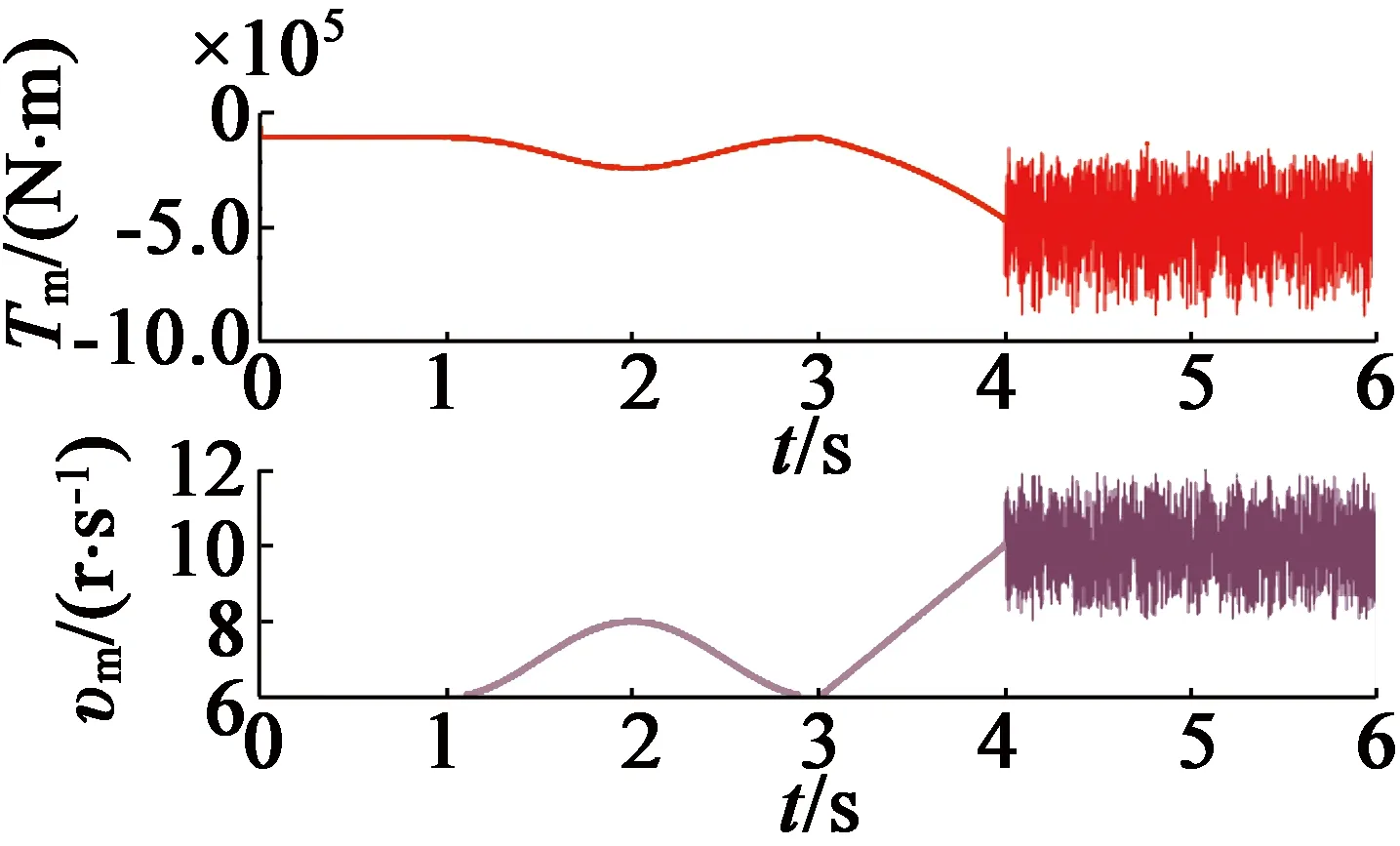
图14 风速υm与机械转矩Tm波形表3 控制器参数

参数数值参数数值kp1-30.7ki1-15.5kp2-50Rski2-1 670Ldkp3-80Rski3-2 670Lq

表3中:kp1,ki1，kp2,ki2，kp3,ki3为转速环与d，q轴电流环的比例与积分增益。

3.3仿真结果及分析

图15为发电机的气隙磁链波形。可知，因变风速扰动导致转速波动，对气隙磁链幅值的影响基本可以忽略，故d，q轴动态解耦参量可为稳态下的电机电感与磁链参量。

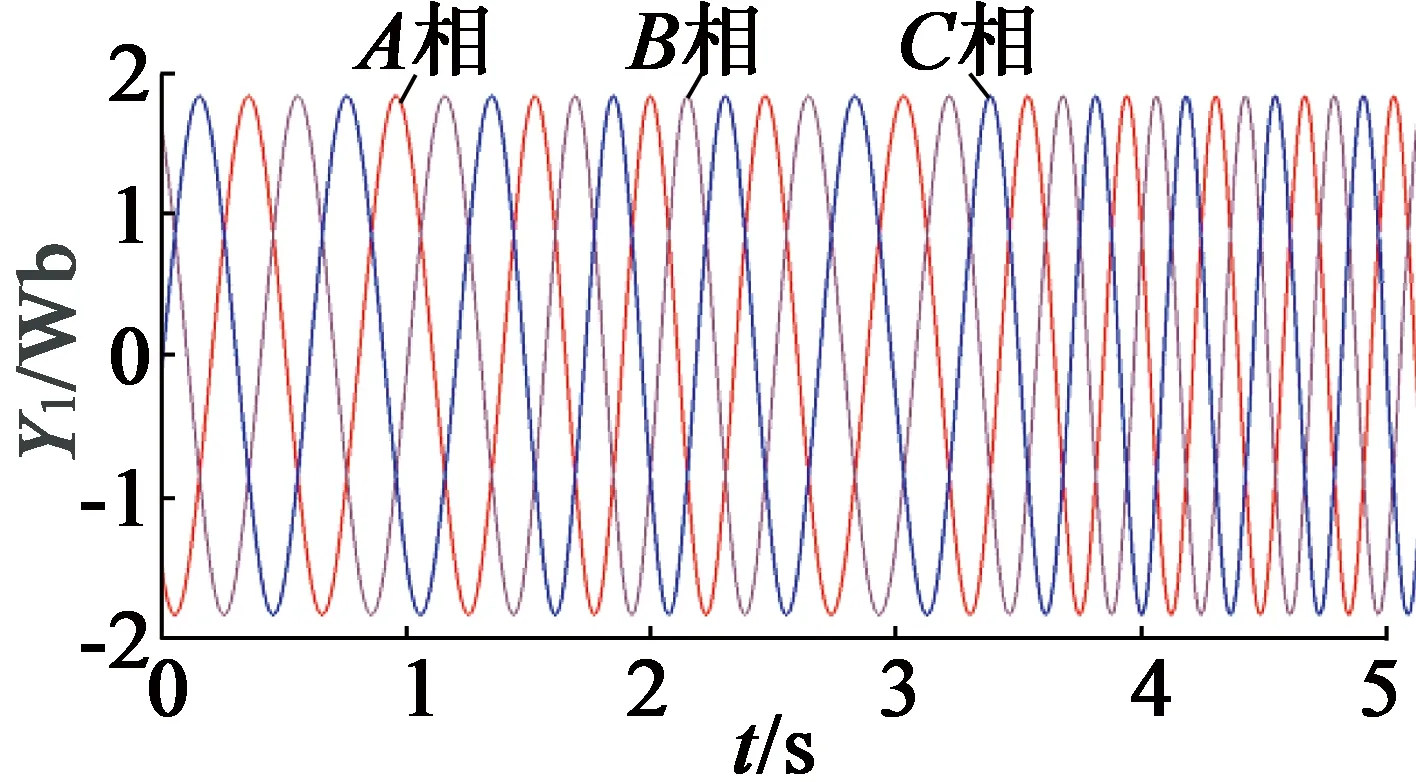
图15 气隙磁链波形

图16为能量系数、发电机机械转速与齿槽转矩波形。发电机采用双闭环PI控制，在四种不同风速下，转速动态响应快，能量系数保持在43.8%。

图16 能量系数Cp、发电机机械转速ωm与Tcog波形

图17、图18为发电机定子电流、转矩与功率波形。可知，通过调节d，q轴电流，使定子电流波形为正弦波，其幅值、转矩与功率快速跟随风速变化，从而实现最大功率追踪。

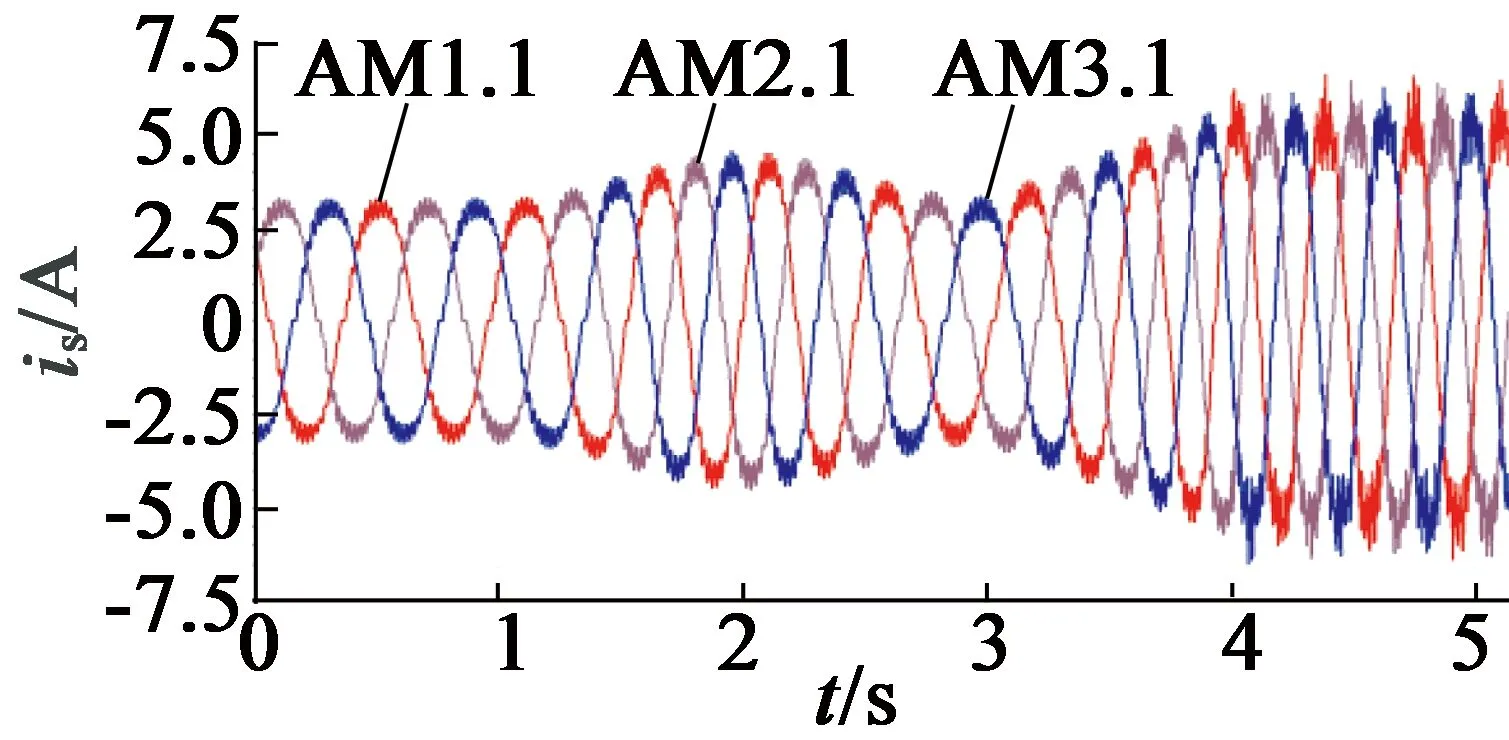
图17 定子电流波形

图18 发电机转矩与功率波形

由图16、图17可见，因风速的高频瞬变干扰，导致PI控制的鲁棒性降低，使能量系数与电流曲线表现为随风速波动剧烈程度增加而增大脉动波形，并产生较大齿槽效应，体现了场路耦合仿真结果的高可靠性。

4 结 语

本文基于电机相似性，针对斜极/斜槽结构的360 kW/690 V，200 r/min永磁发电机性能受多参量耦合影响，研究了利用多变量、多目标耦合优化其尺寸参量，以提升电机效率与转矩，削弱齿槽转矩与谐波；针对PI控制的模型依赖性、兆瓦级风电调试成本高、研制周期长，提出利用有限元法精确建立电机模型，利用场路耦合仿真模拟发电机在四种不同风速扰动、电磁耦合影响参数摄动共同作用下的动态起动过程，并给出了仿真分析，验证了系统实现最大功率追踪可行性，有效提高了仿真结果的可靠性，从而有效降低了硬件调试难度，缩短了硬件研制周期。