基于无传感器的永磁同步电机容错控制

赵柏暄，张 希，钱 伟，张凯炯

(上海交通大学 机械与动力工程学院，上海 200240)

0 引 言

永磁同步电机因其具有功率密度高、效率高、调速范围宽、转矩波动小等优点而成为了电动汽车领域的首选[1]。永磁同步电机的矢量控制需要精确地检测到转子的位置信息，考虑到电动汽车中工作环境较为恶劣，旋转变压器被广泛应用于电动汽车永磁同步电机的位置检测中。

旋转变压器在检测过程中存在故障隐患，这些故障会导致永磁同步电机转矩波动甚至失控，进而会影响车辆行驶的稳定性，甚至会危及车辆安全[2]。因此，有必要采用容错控制以保证电动汽车电驱动系统在旋转变压器发生故障时可以继续运行。Hwang S H等针对旋转变压器的幅值不平衡和正交不完全故障设计了补偿算法[3]，但该方法无法解决旋转变压器断线和短路故障。将无位置传感器控制作为旋转变压器的一种软件冗余，是解决此问题的有效途径。无位置传感器控制算法主要有两类：适用于中高速区的反电动势观测器法，包括递归最小二乘法、扩展卡尔曼滤波器、模型参考自适应法和滑模观测器等；适用于零速、低速区的高频信号注入法，可分为旋转高频电压注入法和脉振高频电压注入法[4]。目前，并没有一种无位置传感器算法可以在全速度范围内对转子位置进行估计。无位置传感器控制技术在永磁同步电机容错控制方面的应用也取得了一定的进展。Demba Diallo等针对车用感应电机设计了一种容错控制算法，该算法由间接矢量控制、基于自适应磁链观测器的无传感器控制及开环V/f控制组成，并提出了一种故障诊断策略，根据诊断结果切换控制算法[5]。Ahmad Akrad等针对永磁同步电机使用扩展卡尔曼滤波器和自适应反电动势观测器对转子位置和速度进行观测，并基于最大似然法设计了故障诊断和容错控制算法[6]。文建平将旋转变压器位置偏差故障补偿算法与基于微分代数观测器的无位置传感器控制算法进行了结合[7]。Gilbert Foo Hock Beng等使用自适应磁链观测器与脉振高频电压信号注入法，实现了全速度范围的容错控制[8]。然而，由于铁心磁饱和、交叉耦合效应及温度等因素的影响，d，q轴电感及永磁体磁链会发生变化[9]。传统的观测器算法依赖于电机参数，当电机参数发生变化时，可能会造成位置估计误差较大等问题。

本文首先分析了旋转变压器故障的影响。其次，针对旋转变压器故障设计了容错控制，在高速区采用基于柔性开关函数滑模观测器的无位置传感器控制算法，在低速区采用脉振高频信号注入法的无位置传感器控制算法及低、高速区过渡算法，并根据估计结果设计了故障诊断算法。最后通过仿真和实验验证了该容错控制算法的有效性。

1 旋转变压器故障影响分析

当旋转变压器存在故障时，可认为测量转子位置与实际转子位置存在角度误差，此时永磁同步电机d，q轴电流可表示:

永磁同步电机的电磁转矩方程:

Te=1.5p[ψfiq+(Ld-Lq)idiq]

(2)

将式(1)代入式(2)，旋转变压器故障状态下永磁同步电机的电磁转矩方程:

Te=1.5pImcosθerr[ψf+(Ld-Lq)Imsinθerr]

(3)

式中：Te为电磁转矩；p为电机极对数；ωr为电机角速度；ψf为永磁体磁链；Im为相电流幅值。

由式(3)可知，在旋转变压器存在故障时，当偏差角度较小时会造成电机输出转矩波动，严重时则可能导致电驱动系统失控，进而会影响车辆的动力性、舒适性和安全性。

2 容错控制

2.1基于高频信号注入的无位置传感器控制算法

假设绕组中的感应电动势为正弦波，在d-q轴同步坐标系中，PMSM的数学模型:

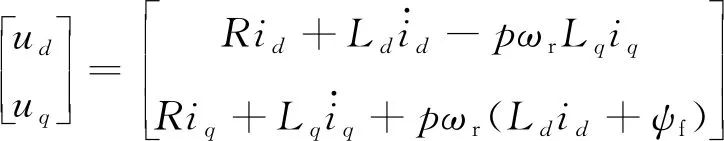
(4)

式中：ud，uq为d,q轴定子电压；id，iq为d,q轴定子电流；R为各相定子电阻；Ld，Lq为d,q轴定子电感。

在低速区，电压注入信号频率远高于基波频率，反电动势可忽略不计，同时忽略定子电阻压降，则PMSM的数学模型可改写：

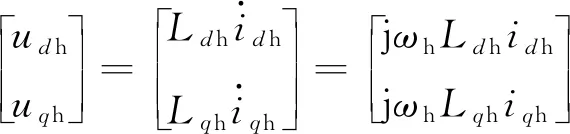
(5)

式中：udh，uqh，idh，iqh，Ldh，Lqh分别为d，q轴高频电压、电流和电感。

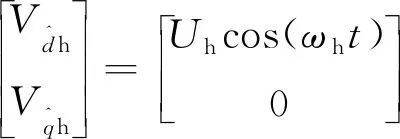
(6)

(7)

将式(7)与sin(ωht)相乘，并通过低通滤波器滤除高频分量，可以得到:

(8)

当Δθ足够小时，可认为:

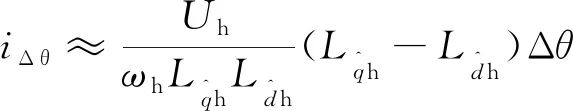
(9)

为获取转子速度和位置信息，观测器设计如图1所示。

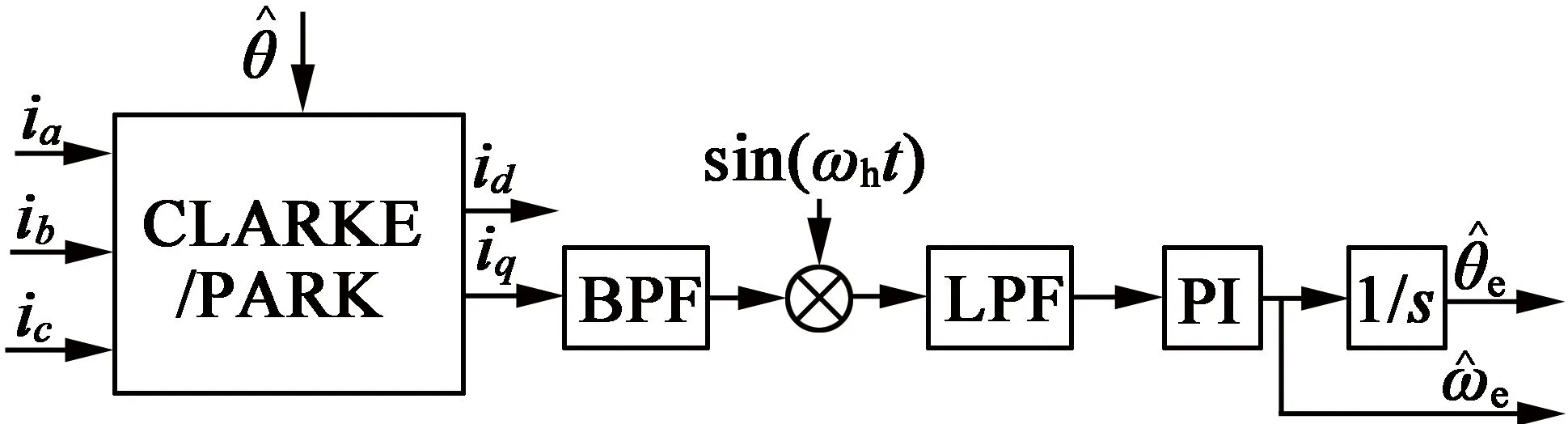
图1 脉动高频电压信号注入法转子位置观测器

2.2基于柔性开关滑模观测器的无位置传感器算法

在α,β坐标系下永磁同步电机的数学模型:

(10)

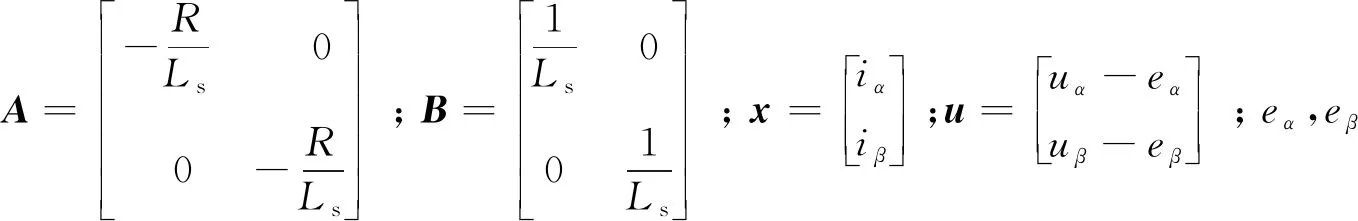
(11)

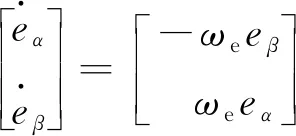
(12)

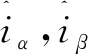
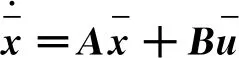
(13)

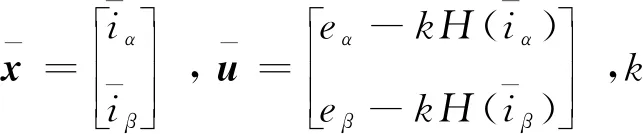
(14)

函数f2∈(0,1]，当UAV的飞行路径上存在点分别与N个信息采集点的坐标之间的距离都在读写器的识别距离之内(即对∀C点都∃点Xi满足1≤r)时，f2的值较小，即所求得的路径较短。

电机转子位置估计值：

(15)

为避免观测器中低通滤波器引起的转子位置估计值相位滞后于实际位置的问题，可采用锁相环提取转子位置信息。基于柔性开关滑模观测器及锁相环的结构如图2所示。

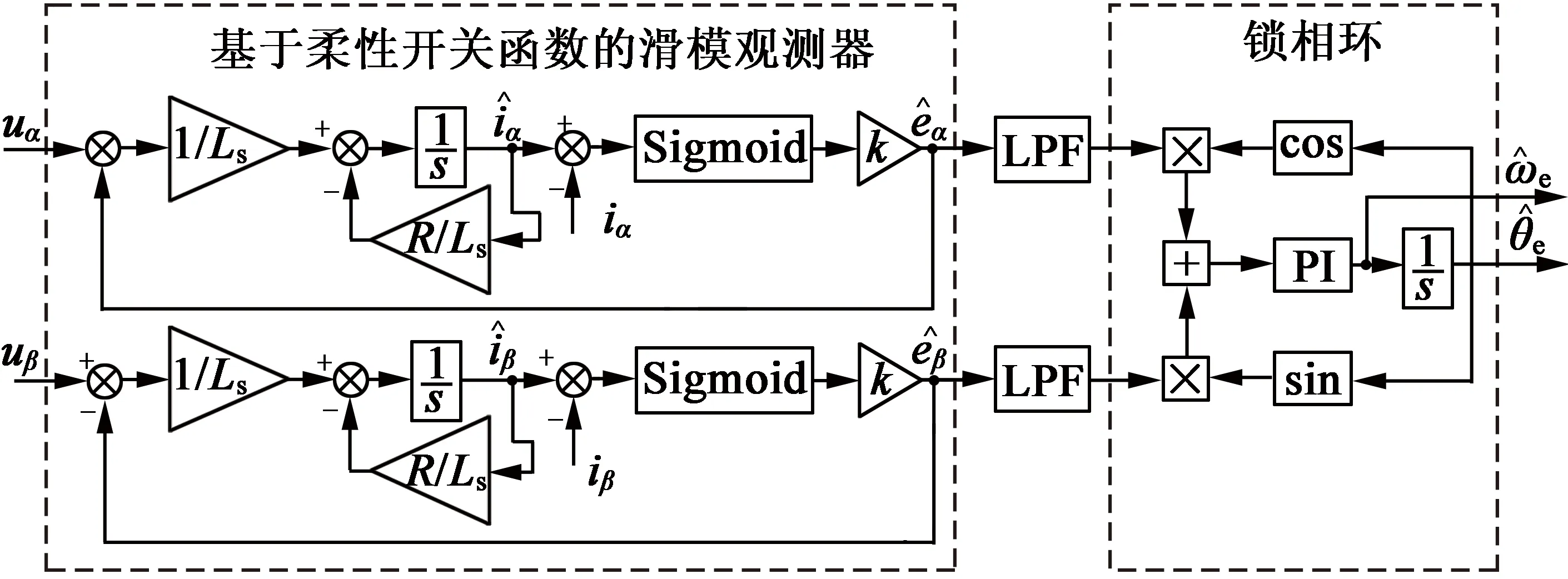
图2 基于柔性开关函数的滑模观测器及锁相环结构

2.3低、高速区过渡算法

如上文所述，为实现全速度范围的无传感器控制，需要在低速区和中高速区分别采用不同的算法。由于脉振高频信号注入法与基于柔性开关滑模观测器的估计结果之间存在误差，直接切换可能会在切换点附近产生振荡。通过权重分配函数作为过渡算法可实现低速区与高速区之间的平稳过渡，权重分配函数设计如下：

(16)

式中：ωL为低速区切换速度点；ωH为高速区切换速度点。

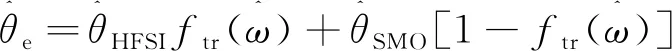
(17)

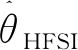
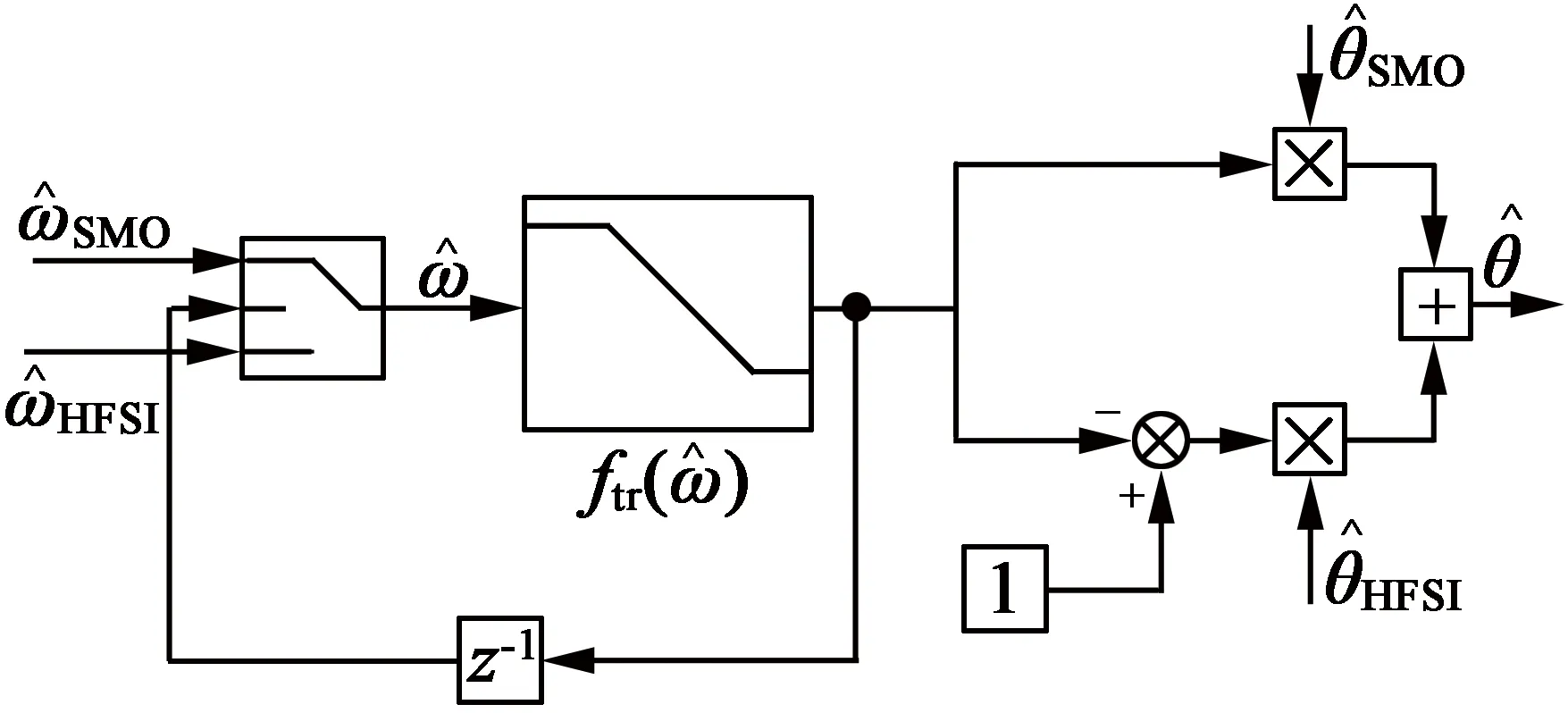
图3 高、低速区过渡算法结构

该过渡算法以估计速度值为过渡算法介入依据，当速度低于低速区切换点时，采用脉振高频信号注入法的估计值；当速度高于高速区切换点时，采用基于柔性开关滑模观测器的估计值；当速度介于两者之间时，进入过渡算法。对于不同车型，该算法均有效，但由于驱动电机不同，切换点需根据具体电机型号确定。

电动汽车传动系通常由单挡减速器或双挡变速器、主减速器及差速器组成。在车辆稳定运行状态下，驱动电机转速和位置可由车速传感器测量结果根据传动系传动比计算得到:

(18)

(19)

所设计的故障诊断判据如下:

(20)

θFLT为位置误差容许值。当转子位置满足式(20)时，则可认为旋转变压器故障，此时使用无位置传感器算法估计值代替旋转变压器测量值，实现容错控制。

3 仿真与实验结果

3.1仿真结果

通过MATLAB-Simulink与CarSim软件建立联合仿真模型。为验证算法的有效性，在仿真测量角度中加入一个偏差角度θerr。图4为不采用容错控制条件下，在0.5 s时旋转变压器发生故障的运行情况。图4中,从上至下分别为电机转子位置、电机输出转矩、车辆纵向加速度。当故障发生时，电机输出转矩波动，进而引起车辆纵向加速度波动，对车辆动力性和舒适性造成不良影响。图5为采用容错控制条件下，在发生故障时电机及车辆运行情况。图5中,从上至下分别为电机转子实际位置和估计位置、转子位置估计误差、电机输出转矩、车辆纵向加速度。由图5可知，转子估计位置与实际位置误差较小，在平稳状态下误差小于0.2 rad,电机与车辆运行平稳。

(a) 电机转子位置

(b) 电机输出转矩

(c) 车辆纵向加速度图4 不采用容错控制运行情况

(a) 电机转子实际位置和估计位置

(b) 转子位置估计误差

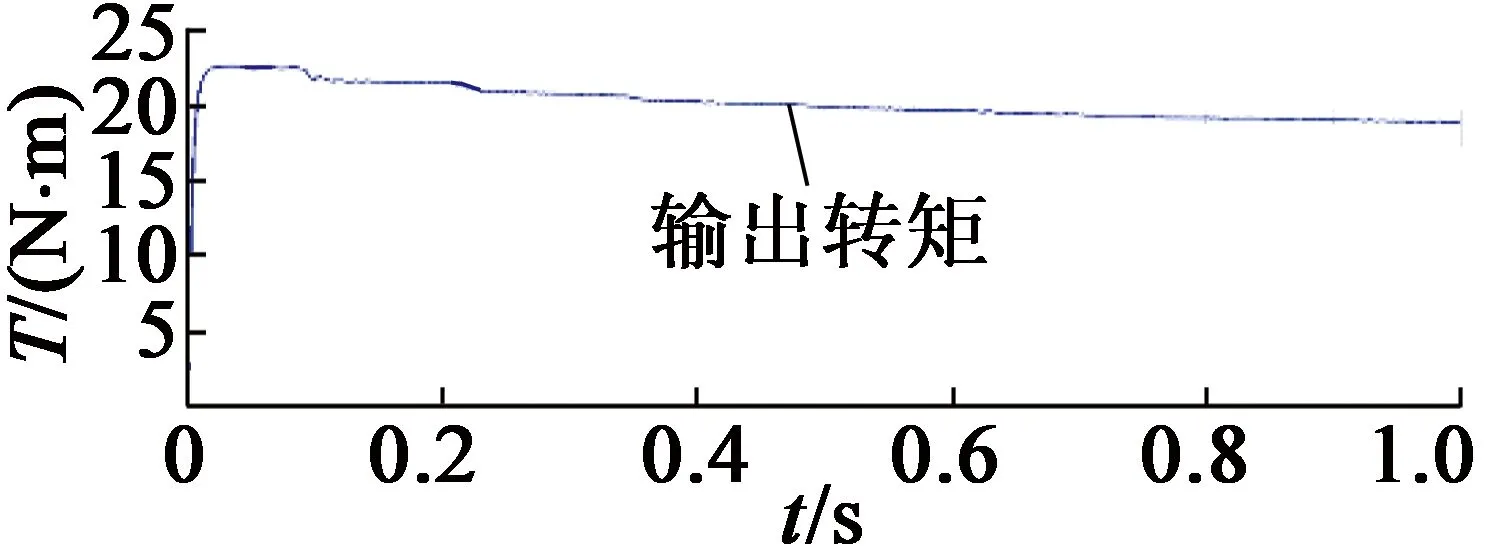
(c) 电机输出转矩

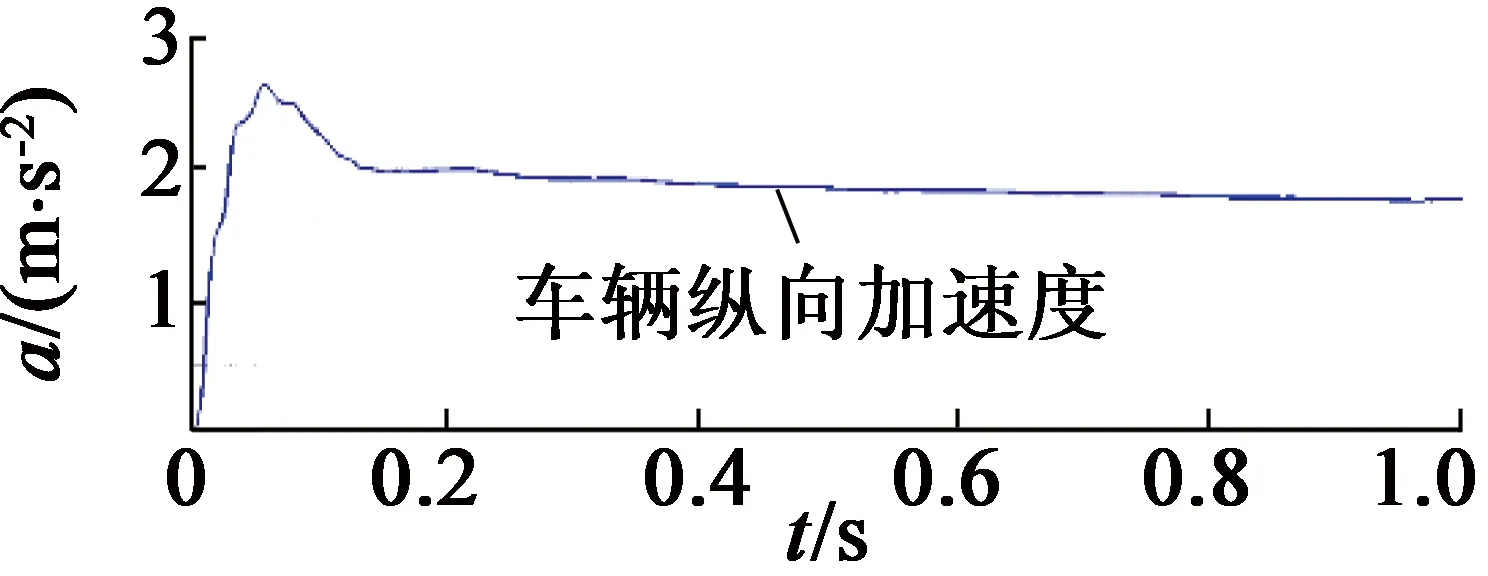
(d) 车辆纵向加速度图5 采用容错控制运行情况

3.2实验结果

使用Micro-AutoBox及1 kW永磁同步电机搭建硬件平台，对所提出的算法进行验证。以一个旋转变压器作为电机转子位置传感器，以另一个旋转变压器采样的位置信息模拟由车速传感器计算得到的转子位置信息，结果如图6所示。

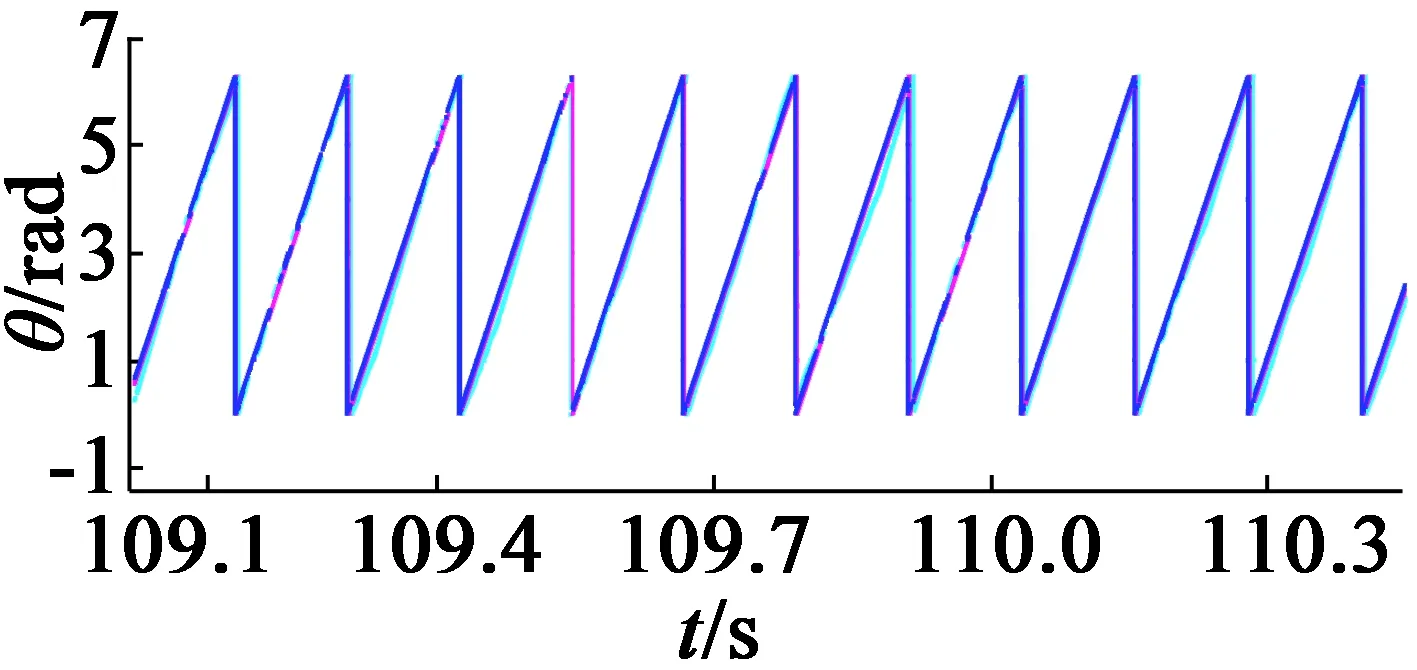
(a) 转子位置估计实验结果

从图6可以看出，估计结果与旋转变压器测量结果之间误差较小，误差主要由传感器测量误差、系统误差及算法中积分累积误差造成。当故障发生时，容错控制可替代旋转变压器提供转子位置信息，维持电机平稳运行。在实际车辆中可采用嵌入式系统作为运行平台，只需在原有电机控制算法中加入该算法，不会额外增加硬件成本。

4 结 语

本文基于脉振高频电压信号注入法及柔性开关滑模观测器设计了永磁同步电动机无传感器控制算法，实现了对转子位置信息的准确估计，并根据估计结果设计旋转变压器故障容错控制算法。仿真及实验结果表明，当不采用容错控制时，旋转变压器故障会对电动汽车电驱动系统及车辆的动力性、稳定性和安全性产生严重危害，本文容错控制算法可有效避免这一问题。