2020年高考电场考题解析

陶汉斌

[摘   要]2020年高考物理试题对电场部分的考查比较突出，既有对基本概念简单应用的考查，又有对综合分析推理能力的考查;既在选择题中出现，也在综合题中出现。其中，对带电粒子在电场中运动问题的考查基调是“电场搭台，力学唱戏”。电场中力与运动，力与能量的关系是高考的热点，常考常新，精彩纷呈。文章分别对以选择题出现的基本概念考题和以综合题出现的分析计算考题进行分析探讨。

[关键词]电场考题;基本概念;综合运用

[中图分类号]    G633.7        [文献标识码]    A        [文章编号]    1674-6058（2020）29-0033-03

电场知识是高中物理的重要组成部分，是每年高考的热点内容，2020年高考对电场知识的考查体现在两个方面，一是考查考生对电场知识理解掌握程度的基本概念题，常以选择题的形式出现;二是考查考生对电场知识综合运用能力的分析计算题，这类题的分值较高。解答好相关考题是夺取高考高分的重要保障。下面结合高考题进行分析解答。

一、电场基本概念考题分析

1.电场的描述——场强与电势

电场的知识非常抽象，我们曾借助检验电荷，从力与能量的两个角度研究电场。当检验电荷静止在电场中某个点时，该电荷受到了电场力并具有一定的电势能，当电荷在电场中从一个位置移动到另一位置时，体现了做功的过程与能量的变化。从力的角度引入了电场强度[E]的概念，用来描述电场;利用电势[φ]与电势差[U]，从做功与能量的角度来描述电场。

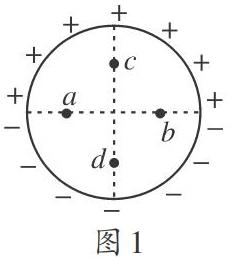
[例1]（2020年全国卷Ⅱ）如图1，竖直面内一绝缘细圆环的上、下半圆分别均匀分布着等量异种电荷。a、b为圆环水平直径上的两个点，c、d为竖直直径上的两个点，它们与圆心的距离均相等。则（）。

A. a、b两点的场强相等

B. a、b两点的电势相等

C. c、d两点的场强相等

D. c、d两点的电势相等

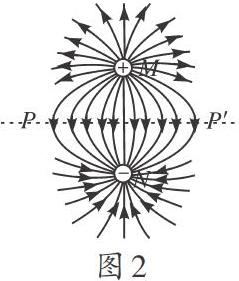
解析：如图2所示，学生都知道等量异种电荷周围空间的电场线分布情况。该题情景中的带电圆环，可等效拆解成这样无数对等量异种电荷的电场，它们在竖直方向上平行放置。中轴线为[PP]，它所在的水平面与每一条电场线都是垂直的，也就是等势面，将这些等势面延伸到无穷远处，无穷远处电势为零。

根据对称的特点，中轴线[PP]上所有点的电势均为零，即[φa=φb=0];沿着点M走到点N，从正电荷走到负电荷，电势一直在降低，即[φc>φd]，故B正确，D错误;而对于A、C两个选项，在图中，观察可知上下两侧电场线分布对称，左右两侧电场线分布也对称，由电场的叠加原理可知A、C正确。本题的正确选项为ABC。

点评：场强的叠加是矢量运算，而电势的叠加是标量相加，正电荷周围电势大于零，而负电荷周围电势小于零。注意电场的对称性。

电场是客观存在的、物质的，但它非常抽象，学生很难想象在一个空间有那么一个电场，既看不到又摸不着。可就是这个电场有力的性质和能的性质。为帮助学生理解电场强度和电势等抽象概念，引入了形象描述电场的方法——电场线与等势面，以达到由形象思维上升到抽象思维的境界。当然，电场线与等势线是有关系的，如电场线与等势线处处垂直正交，电场线的方向是从电势较高的等势面指向电势较低的等势面，等差等势面的疏密定性代表了电场强度的大小，等差等势面越密定场强越强，等差等势面越疏场强越弱。

2.两条图线——电场线与等势线

电场是客观存在的物质，但又是看不见摸不着的。不像力学中弹簧、小车、小球等有具体形象的物理模型，因此在研究电场问题时，为了更加形象直观地描述电场，从电场强度的角度引入了电场线，以描述场强[E];从电势的高低引入了等势线与等势面，以达到由形象思维上升到抽象思维的境界。

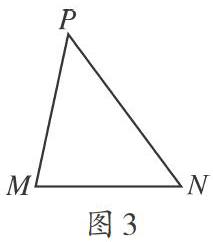
[例2]（2020年全国卷Ⅲ）如图3，∠M是锐角三角形PMN最大的内角，电荷量为[q（q>0）]的点电荷固定在P点。下列说法正确的是（）。

A. 沿MN边，从M点到N点，电场强度的大小逐渐增大

B. 沿MN边，从M点到N点，电势先增大后减小

C. 正电荷在M点的电势能比其在N点的电势能大

D. 将正电荷从M点移动到N点，电场力所做的总功为负

解析：A.点电荷的电场以点电荷为中心，向四周呈放射状，如图4，[∠M]是最大内角，所以[PN>PM]，根据点电荷的场强公式[E=kQr2]（或者根据电场线的疏密程度）可知从[M→N]电场强度先增大后减小，故选项A错误;B.电场线与等势面（图中虚线）处处垂直，沿电场线方向电势降低，所以从[M→N]电势先增大后减小，故选项B正确;C. [M]、[N]两点的电势大小关系为[φM>φN]，根据电势能的公式[Ep=qφ]可知正电荷在[M]点的电势能大于在[N]点的电势能，故选项C正确;D. 正电荷从[M→N]，电势能减小，电场力所做的总功为正功，故选项D错误。本题的正确选项为BC。

点评：电场线与等势线是用来直观描述电场的图线，我们在解题时要善于借助图线进行解题。

二、电场知识综合运用考题分析

在學习物理的过程中学生要建立三大物理观念，也就是力、运动以及能量的观念。高考物理重点考查力与运动的关系，力与能量的关系，考查学生的综合分析能力。

[例3]（2020年全国卷Ⅰ）在一柱形区域内有匀强电场，柱的横截面积是以O为圆心，半径为R的圆，AB为圆的直径，如图5所示。质量为m，电荷量为[q（q>0）]的带电粒子在纸面内自A点先后以不同的速度进入电场，速度方向与电场的方向垂直。已知刚进入电场时速度为零的粒子，自圆周上的C点以速率v0穿出电场，AC与AB的夹角[θ=60°]。运动中粒子仅受电场力作用。

（1）求电场强度的大小;

（2）为使粒子穿过电场后的动能增量最大，该粒子进入电场时的速度应为多大？

（3）为使粒子穿过电场前后动量变化量的大小为[mv0]，该粒子进入电场时的速度应为多大？

解析：（1）粒子初速度为零，由C点射出电场，故电场方向与AC平行，由A指向C。由几何关系和电场强度的定义知：

（2）如图6，由几何关系知[AC⊥BC]，故电场中的等势线与BC平行。作与BC平行的直线与圆相切于D点，与AC的延长线交于P点，则自D点从圆周上穿出的粒子的动能增量最大。由几何关系知：

设粒子以速度v1进入电场时动能增量最大，在电场中运动的时间为t1。粒子在AC方向做加速度为a的匀加速运动，运动的距离等于AP;在垂直于AC的方向上做匀速运动，运动的距离等于DP。由牛顿第二定律和运动学公式有：

（3）设粒子以速度v进入电场时，在电场中运动的时间为t。以A为原点，粒子进入电场的方向为x轴正方向，电场方向为y轴正方向建立直角坐标系。由运动学公式有：

粒子在电场中运动时，其x方向的动量不变，y方向的初始动量为零。设穿过电场前后动量变化量的大小为[mv0]的粒子，离开电场时其y方向的速度分量为v2，由题给条件及运动学公式有：

此题中的第三个问题还有另外一种解法：由题意知，初速为0时，动量增量的大小为[mv0]，此即问题的一个解。自A点以不同的速率垂直于电场方向射入电场的粒子，沿y方向位移相等时，所用时间都相同。因此，不同粒子运动到线段CB上时，动量变化都相同，自B点射出电场的粒子，其动量变化也为mv0，由几何关系及运动学规律可得，此时入射速率[v=32v0]。

点评：此题考查了带电粒子在电场中的运动问题，我们可运用运动的独立性和力的独立作用原理进行分析。第三问的另解中运用了等效的思维方法。

[例4]（2020年新课标全国卷）某型号质谱仪的工作原理如图7甲所示。M、N为竖直放置的两金属板，两板间电压为U， Q板为记录板，分界面P将N、Q间区域分为宽度均为d的Ⅰ、Ⅱ两部分，M、N、P、Q所在平面相互平行，a、b为M、N上两正对的小孔。以a、b所在直线为z轴， 向右为正方向，取z轴与Q板的交点O为坐标原点，以平行于Q板水平向里为x轴正方向，竖直向上为y轴正方向，建立空间直角坐标系Oxyz。区域Ⅰ、Ⅱ内分别充满沿x轴正方向的匀强磁场和匀强电场，磁感应强度大小、电场强度大小分别为B和E。一质量为m，电荷量为+q的粒子，从a孔飘入电场（初速度视为零），经b孔进入磁场，过P面上的c点（图中未画出）进入电场，最终打到记录板Q上。不计粒子重力。

（1）求粒子在磁场中做圆周运动的半径R以及c点到z轴的距离L;

（2）求粒子打到记录板上位置的x坐标;

（3）求粒子打到记录板上位置的y坐标（用R、d表示）;

（4）如图7乙所示，在记录板上得到三个点s1、s2、s3，若这三个点是质子[11H]、氚核[31H]、氦核[42He]的位置，请写出这三个点分别对应哪个粒子（不考虑粒子间的相互作用，不要求写出推导过程）。

解析：（1）设粒子经加速电场到b孔的速度大小为v，粒子在区域Ⅰ中做匀速圆周运动，对应的圆心角为α，在M、N两金属板间，由动能定理得：

（4）根据已求得的竖直位移可知，荷质比越大，竖直位移越大，所以s1、s2、s3分别对应氚核[31H]、氦核[42He]、质子[11H]的位置。

点评：本题考查带电粒子在电场和磁场中的运动，在电场中带电粒子做直线运动与类平抛运动，可用动能定理和运动的独立性原理进行分析求解，在解题时要注意运动的立体三维空间。

三、科学的思维方法

前面我们剖析了高考对电场知识的考查，高考要求考生在掌握物理知识的同时，也应该关注重要的科学研究方法，旨在培养考生的科学研究能力（这是考生终身受用的本领）。只有这样才能提高学生的物理学科素养。在电场这一章的教学过程中发现其中蕴藏着许多科学研究方法。具体表现在如图8的框图中。

在电场这一章的教学过程中，我们可利用类比研究的方法，将必修一与必修二所学过的方法迁移到抽象的电场中。如电场这一章中，万有引力定律與库仑定律的类比，重力场与电场中的力做功以及能量的类比，电场中的类平抛运动与重力场中的平抛运动进行类比。类比是一种逻辑推理形式，是一种极具启发性、创造性、灵活性的推理方法。应用两种物理现象和两种物理规律之间的相似或相同，推出其他方面也相似或相同的方法就是类比法。在物理学研究陷入困境时，通过类比方法往往能打开一个新的天地。每当理智缺乏可靠的论证思路时，类比法往往能指引我们前进。

（责任编辑 易志毅）