基于新课标理念的数学教学设计与思考

[摘 要] 基础知识的扎实、基本技能的熟练是数学应用的基础，也是学生后续学习的基础.数学思想蕴含在数学知识形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概括.在数学教学中，教师应引导学生积极参与教学活动，让学生通过独立思考、合作交流，逐步感悟数学思想，积累数学活动经验.

[关键词]中考第一轮复习;教学设计;平行四边形

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2020）29-0014-03

中考第一轮复习是对所复习的知识点进行系统的整理，把复习前孤立、分散、无序、认知模糊的概念及解题的思路，以再现、整理、归纳等方法串成线、连成片、结成网，使其成条理化、系统化的知识网络、知识框架.这也是对已学知识查缺补漏，让学生从数学的复习中获得乐趣，从整体上理解和掌握知识间的内在联系，促进学生对知识的重新消化，便于以后理解和应用.如果说平时的讲授新课主要任务是以“基础知识”的掌握以及“基本技能”的形成为主，那么通过复习在进一步巩固原来的“双基”的同时，更加注重数学“基本思想”的提炼以及“基本活动经验”的积累.

一、教学设计

教学环节一 回顾旧知，激活已有知识经验

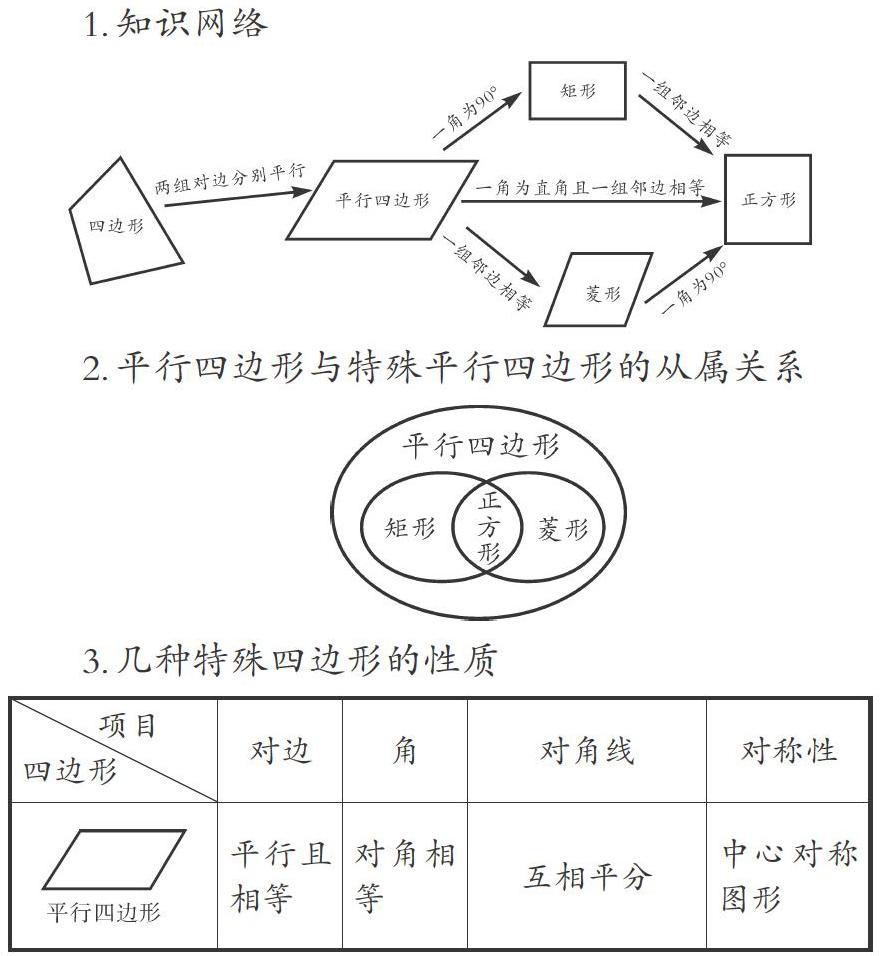
多媒体呈现以下知识内容，引导学生回顾旧知，激活学生已有的知识经验.

1.知识网络

2.平行四边形与特殊平行四边形的从属关系

3.几种特殊四边形的性质

4.特殊四边形的常用判定方法

跟踪练习1：（中考·淄博）已知?ABCD，对角线AC、BD相交于点O.①请你添加一个适当的条件，使?ABCD成为一个菱形，你添加的条件是___________; ②请你添加一个适当的条件，使?ABCD成为一个矩形，你添加的条件是___________; ③要使?ABCD成为一个正方形，需要添加___________个条件，你添加的条件是___________.

教学组织及意图：本环节首先通过多媒体呈现“知识网络”“平行四边形与特殊平行四边形的从属关系”，利用图示及表格直观表达的方式带领学生从整体上获得感性认识;接着师生互动，共同完成学生手中的“四边形的相关知识清单”，激活学生已有的知识经验，为进一步激发学生数学活动经验做好铺垫. “跟踪练习1”的设计具有开放性， 很好地检查了学生对几个“特殊平行四边形”概念的理解和掌握.

教学环节二   交流合作，师生互动

[例1]如图2，在△ABC中，点P是BC边上的动点，过点P作PD//AB交AC于D，PE//AC交AB于E.

问题1：四边形AEPD是什么特殊四边形？

问题2：四边形AEPD可能是菱形、矩形、正方形吗？

问题3：当P运动到何处时，四边形AEPD为菱形？说明理由.

问题4：若四边形AEPD为菱形时，AP有何特点？

问题5：根据以上研究获得成果，你能用一张三角形纸片只折2次，折出一个菱形吗？若能，请说明你的折法和理由.

问题6：当△ABC满足什么条件时，四边形AEPD为矩形？

问题7：当点P运动到何处且△ABC满足什么条件时，四边形AEPD为正方形？

跟踪练习2：

1. （中考·兰州）平行四边形ABCD的对角线AC与BD相交于点O，且AC⊥BD，请添加一个条件：___________，使得平行四边形ABCD为正方形.

2.（中考·贺州）如图3，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF.

（1）求证：四边形AECF是菱形;

（2）若AB=[3]，∠DCF=30°，求四边形AECF的面积（结果保留根号）.

教学组织及设计意图：例1的设计本着一题多用的原则，从问题出发，以解决问题为切入点.问题1的设计起点低，目的是提高学生思考的积极性.问题2、问题3 提高了一个档次，用动点P带动四边形AEPD的变化来串联知识点.问题4换了一个角度，考查四边形AEPD为菱形时线段AP的变化.问题6、问题7从图形的整体去考虑问题：当△ABC满足什么条件时，四边形AEPD为矩形;点P运动以及当△ABC满足什么条件时四边形AEPD为正方形.如果说问题1、2、3、6、7是让学生大脑动起来，那么问题5则是既要学生动脑又要学生动手.教师在教学中不能忽视动手操作的作用.操作与思考相结合，对于发展学生的空间观念与推理能力是必不可少的.应让学生经历观察、操作的过程来加深对复习内容的理解和掌握.

教学活动及设计意图：例2的设计是隐去结论，只出示条件 ，引导学生思考，让学生充分发挥想象力：由在“矩形ABCD中，O为AC的中点”联想到“OB为Rt△ABC斜边AC的中线”进而联想到定理“直角三角形斜边上的中线等于斜边的一半”，从而得出结论OB=BC，再由 “[∠COB=60°]”得出△OBC是等边三角形;另外，根据题目的已知条件以及所给的图形还能得出“[△FCO≌△EAO”]“四边形DEBF是平行四边形”以及“△DEF是等边三角形”……让学生充分开动脑筋，根据自己已有的知识储备，尽可能地得出更多的结论.然后再出示該题的要求.本题具有一定的挑战性，目的是激发学生的探究欲望.实践证明，这样处理能较好地调动学生的学习积极性，启发学生的思维，进一步提高学生的探究能力以及合情推理能力.

教学环节三   课堂小结

（1）知识点：回到开始环节中的“知识网络”“平行四边形与特殊平行四边形的从属关系”以及几个特殊平行四边形的性质及判定.

（2）数学思想方法：①分类思想;②化归思想;③数形结合思想.

（3）思维方式：①发散性思维; ②逆向思维.

（4） 知识迁移：①“知识网络”;②动点.

（5）情感、态度与价值观：①勤学善思，乐于合作;②引发好奇心与求知欲;③克服困难，建立自信.

教学组织及设计意图：课堂小结是一节课学习的升华与深化，是一个非常重要的教学环节.课堂小结，不是单一的知识点的罗列，还应从数学思想方法获取、技能提升、能力发展、学习习惯培养、学习方法改进等方面进行梳理和反思. 通过课堂总结，强调相关知识点和数学思想方法以及解题经验等，旨在引导学生反思自己的学习过程，加深学生对本节重点知识的理解，关注基本数学活动经验的再积累.

教学环节四   布置作业，巩固所学知识（略）

二、教后思考

1. 精心“组织”

教师的“组织”作用主要体现在两个层面：第一，“组织”教学内容.教师应当准确把握数学教学内容的实质和学生的实际情况，确定合理的教学目标，设计一个好的教学方案.本节课的教学内容是复习“特殊四边形”——矩形、菱形以及正方形，由于是中考前第一轮复习，所以一方面要进行相关图形的概念、性质和判断方法的复习，另一方面要对学生积累的相关数学经验进行“激发”.在教学第一环节中，首先从知识的宏观层面——“知识网络”展开，接着运用“集合图”，形象地展示“平行四边形与特殊平行四边形的从属关系”，最后再具体到几类“特殊平行四边形的性质及判定方法”.这样的安排比一上来就复习几类特殊平行四边形的定义、性质及判定方法要好得多：通过这个环节的学习，学生更容易从整体上来建构知识网络.本节课的核心环节——“师生互动，合作探究”，所选取的例题及“跟踪练习”均为云平台资源上面提供的典型中考试题，让学生零距离体验一把中考.第二，“组织”教学活动.教师要选择适当的教学方式，因势利导、因材施教、适时调控，努力营造师生互动、生生互动的生动活泼的课堂氛围，形成有效的学习活动.

2.适时“引导”

教师的“引导”作用主要体现在：通过恰当的问题，或者准确、清晰、富有启发性的讲授，引导学生积极思考、求知求真，激发学生的好奇心; 特别要引导学生自主参与知识整理，在整理知识的过程中，进行知识编码，对自己的认知结构实行精加工，使平时所学的“分散、零乱、细碎”的知识点结成知识链，形成知识网，让学生的思维得到再一次发展与生长.例1中的七个问题的设计从问题出发，以解决问题为切入点，借助问题串把平行四边形及特殊的平行四边形来个大盘点、大串联，其间，学生猜想、质疑、讨论、动手操作验证、动口（手）进行推理论证，层层推进，不断挑战自我，从多角度探索、发现、推理，在发现问题、提出问题、分析问题、解决问题（四能培养）中，提升学生的数学素养.本题设计起点低、落点高，引导学生在思维的山路上不断向上攀爬，可谓思维“节节高”！

3.剑指“四基”

《义务教育数学课程标准（2011年版）》明确指出：“通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验.”基础知识的扎实、基本技能的熟练是数学应用的基础，是学生后续学习的基础， 数学思想蕴含在数学知识形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概括，如抽象、分类、归纳、演绎、建模等.学生在积极参与教学活动的过程中，通过独立思考、合作交流，能逐步感悟数学思想，积累数学活动经验.积累数学活动经验重在“做”，“数学活动经验”是在“做”中慢慢积累起来的. 例1中的“问题 5：根据以上研究获得成果，你能用一张三角形纸片只折2次，折出一个菱形吗？若能，请说明你的折法和理由”让学生通过自己的实践、猜测、验证，发现问题、研究问题和解决问题，在这个操作过程中，学生不仅仅是进一步掌握了相关的知识，还积累了如何去发现问题、如何去研究问题的经验.例2教学，只出示了题目，给出条件，隐去结论，放手让学生去展开联想，发现其中的正确结论，落实“见图想性质（看图说话）”“见条件想结果（华罗庚的推想法）”，为不同水平的学生提供参与的机会，引导他们先去“合作交流”，让他们都有话可说;然后再出示结论，实现师生间的合作、交流，和学生一起去分析、研究从结论中如何下手，探寻破题之路，让学生尝试推理论证，小组互助、合作，采用“兵教兵”的办法：优等生为学困生疏导思路，解决问题，同时优等生的数学素养得以提升，实现“学学相长”，为每个学生的智慧生成蓄能.

三、写在最后

中考复习课是一首老歌，但是复习课并非单纯的知识重述，而应是知识点的重新整合、深化、升华，复习课更应该是重视发展学生的数学思维能力，巩固旧知，是为了获取新知，在巩固旧知的基础上要给学生以新的收获，即“在练中学”.

[   参   考   文   献   ]

[1]  刘钰.探究奇妙的“黄金三角形”：基于微课理念下的教学设计与思考[J].中学数学，2018（20）：8-9.

[2]  吕学江. 走进名师课堂 [M].济南：山东人民出版社，2011.

[3]  教育部基礎教育课程教材专家工作委员会.义务教育数学课程标准（2011年版）解读[M].北京：北京师范大学出版社，2012.

（责任编辑 陈   昕）