数学核心素养的评价模型研究*

摘   要   数学核心素养评价不同于以知识掌握为考核目标的考试，需要综合考虑多种因素。研究构建了6个一级指标14个二级指标的数学核心素养评价模型，并通过调查问卷，确定每一个评价指标的内涵及其权重。研究结果发现，该评价模型的构建具有一定的信度和效度，数学核心素养评价的指标既相互联系又相对独立，具有整体性、变化性和递进性等特点。

关键词   数学核心素养  评价指标  层次分析  权重  关系矩阵  模型

一、研究背景

近年来，核心素养研究受到了教育领域的广泛关注。DeSeCo项目团队指出：核心素养是覆盖多个生活领域、促进成功生活和健全社会的重要素养[1]。从学科层面而言，数学核心素养指学生通过数学学习，养成的品格和能力，以形成终身发展的可持续动力，并不断适应社会发展的需要。在《普通高中数学课程标准（2017年版）》（以下简称新课标）中，提出数学核心素养的六个要素—数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析，并将数学核心素养划分为3个水平[2]。在新课标修订的过程中，主要新增了数学学科核心素养和学业质量标准两部分内容。新课标发布后，数学学科核心素养的评价广受关注。

在已有研究的基础上，以新课标提出的数学核心素养的六个要素作为评价一级指标，提出研究的主要问题：学生数学核心素养评价包括哪些二级指标？一级评价指标与二级评价指标的关系如何？各个评价指标的具体内涵如何？怎样构建数学核心素养评价模型？首先，分析学习评价指标和模型。其次，构建数学核心素养评价的指标体系。最后，探究各个二级评价指标在一级评价指标体系中所起的作用及相应的权重。尝试建立数学核心素养评价模型，以期根据学生在各个指标上的表现，来判断和评价学生数学核心素养发展水平。

二、研究方法

1.被试选择

（1）初测被试

采用随机取样方法，在第二届全国数学教育哲学暨数学教育高层论坛会议期间，邀请部分参会人员参加调查。被试合计62人，其中，数学教育研究专家49人，数学课程与教学论专业在读研究生13人;数学核心素养评价二级指标咨询意见表全部收回。

（2）复测被试

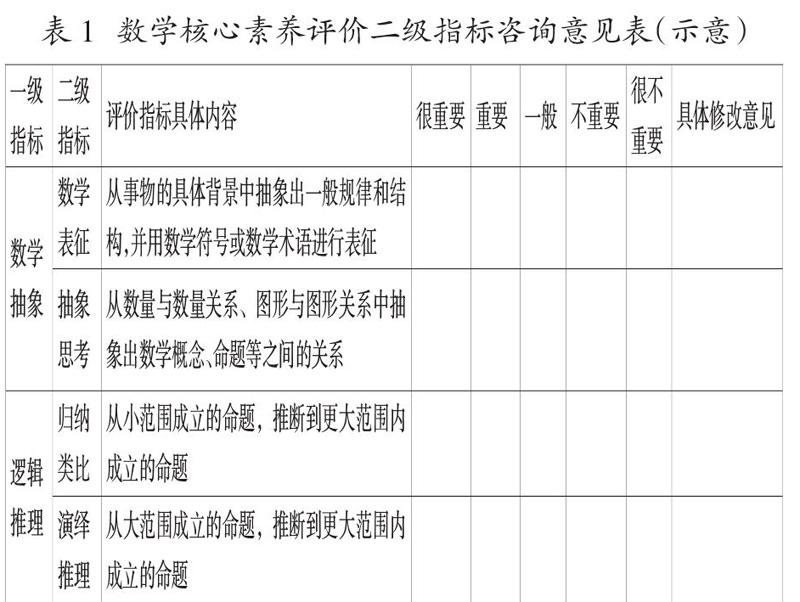
在第二届全国数学教育哲学暨数学教育高层论坛结束之后，从参会人员中，抽取未参与初测的其他数学教育研究者参与调查，调查采用网络问卷的形式进行。表1为调查所用咨询意见表。

参与网络问卷调查的被试合计32人，其中，数学教育研究专家28人，数学课程与教学论专业在读研究生4人;数学核心素养评价二级指标咨询意见表全部收回。

2.研究工具

（1）初测工具

对数学核心素养评价指标进行分析，自编《数学核心素养评价二级指标咨询意见表》的初测版，该问卷共6个一级指标，14个二级指标，采用Likert5点计分法。

（2）复测工具

根据初测情况，对部分二级评价指标具体内涵进行调整，自编《数学核心素养评价二级指标咨询意见表》的复测版。数学核心素养评价一级指标（二级指标）具体内容如下：数学抽象（数学表征、抽象思考），逻辑推理（合情推理、演绎推理），数学建模（问题提出、模型建构、解释验证），数学运算（运算法则、运算策略），直观想象（几何直观、空间想象），数据分析（获取数据、加工数据、解释数据）。

3.统计方法

采用Excel2013管理数据库，使用Yaahp.10.3软件对数据进行层次分析。同时，使用SPSS22.0进行信度、效度分析。

三、研究过程及结果

1.评价指标确立与设计

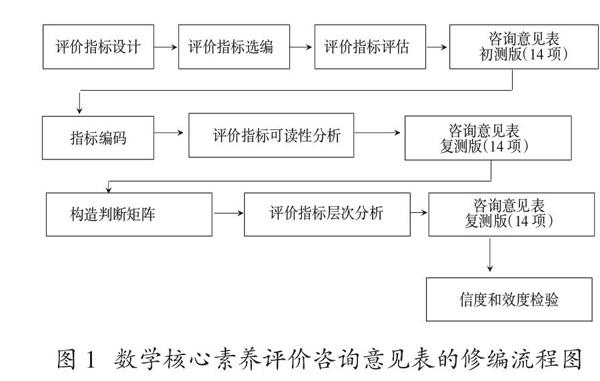
数学核心素养（key competences）是学生应具备的、能够适应终身发展和社会发展需要的、与数学有关的关键能力和思维品质。它与人的行为相关，也是数学教育的终极目标，即引导学生用数学的眼光观察世界、用数学的思维思考世界、用数学的语言表达世界。数学核心素养的评价指标主要包括6个一级评价指标：数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析。在评价指标确立后，进行测试问卷的编制，具体流程如图1。

2.评价指标选定与评估

（1）评价指标选定

在评价指标的选定过程中，充分考虑核心素养、学科核心素养与数学学科特点，既能够反映数学学科知识内容，又能体现数学学科核心素养的特点。在数学核心素养评价指标的表述上，尽量做到通俗易懂、简洁准确。

（2）评价指标评估

评价指标初步拟定后，请南京师范大学数学课程与教学论专业的教師，以及部分研究生评价这些项目。主要评价两个方面的内容：一是评价指标的表述是否涵盖了该指标的内涵，二是评价指标是否符合数学学科知识实际，以及教师对核心素养等概念的理解等。通过指标选定和评估工作，最终确定了《数学核心素养评价二级指标咨询意见表》的初测版。

3.初测与评价指标分析

采用自编《数学核心素养评价二级指标咨询意见表》的初测版，该量表共14个项目，每个项目均使用Likert5点记分法，1表示“很不重要”，2表示“不重要”，3表示“一般”，4表示“重要”，5表示“很重要”。从第二届全国数学教育哲学暨数学教育高层论坛参会人员中，随机抽取数学教育研究者参与调查。

（1）评价指标编码

将《数学核心素养评价二级指标咨询意见表》的6个一级指标之下的14个二级指标，分别在字母后加上序号1、2、3加以区分，如V1、V2、V3等。

（2）评价指标可读性评价

随后，请62名数学教育研究者，对意见表的可读性进行评价。对意见表中的每个项目采用Likert5点计分法（1-5分别表示完全明白、基本明白、不确定、基本不明白、完全不明白）。可读性评估结果表明，多数研究者对意见表“完全明白”（82%）或者“基本明白”（15%）。

根据量表评定结果，结合访谈，对指标进行如下修改。

①指标2“抽象思考”（V2）“有一定的抽象能力，并能建立具体情境与数学问题之间的关联”，部分研究者认为指向不够具体，修改为“从数量与数量关系、图形与图形关系中抽象出数学概念、命题等之间的关系”。

②指标3“合情推理”（V3）、指标4“演绎推理”（V4）“从小范围成立的命题，推断到更大范围内成立的命题”、“从大范围成立的命题，推断小范围内也成立的命题”表述的内容只涉及命题，修改为“从已有的事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果”、“从已有的事实（包括定义、公理、定理等）和确定的规则（包括运算的定义、法则、顺序等）出发，按照逻辑推理的法则证明和计算”。

③指标7“解释验证”（V7）“用数学方法得到结论，验证数学结论与实际问题的相符程度”表达不便于理解，修改为“求解结论、验证结果，反思和改进模型，最终解决问题”。

④指标9“运算策略”（V9）“选择合适的运算策略，简化运算过程的能力”表达太过笼统，修改为“选择运算方法，设计运算程序，得到运算结果”。

⑤指标11“空间想象”（V11）“利用空间观念，想象认知事物的形态与变化”表述不够明晰，修改为“对客观事物的空间形式进行观察、分析和抽象的能力”。

⑥指标13“加工数据”（V13）、14“解释数据”（V14）“利用各类图表，表示数据的能力”、“解释数据，获取知识的能力”表述不便于理解，修改为“利用各类图表表示数据，构建模型分析数据”、“解释数据蕴含的结论”。

通过以上的指标分析，最终确定了《数学核心素养评价二级指标咨询意见表》的复测版。

4.复测与评价指标层次分析

采用《数学核心素养评价二级指标咨询意见表》的复测版，该量表共6个一级指标、14个二级指标。在第二届全国数学教育哲学暨数学教育高层论坛结束之后，采用网络问卷的方式，从参会人员中随机选取32名数学教育研究者参与调查。

由于《数学核心素养评价二级指标咨询意见表》的初测和复测版只有指标具体内涵的变化，而一级指标、二级指标数量没有变化，所以将两次统计的样本数据合并（N=62+32=94）。虽然该样本数不是太大，但通过学习苏洪雨[3]、桂德怀[4]对学生几何素养、代数素养的评价研究，该样本数基本符合构建评价模型的要求。

（1）数学核心素养评价指标的模型建构

运用Yaahp.10.3软件进行评价指标权重系数的分析，建构层次结构模型，模型由3个层次构成。

最上层为目标层：数学核心素养。

第二层为一级指标层：数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析。

第三层为二级指标层：数学表征、抽象思考;合情推理、演绎推理;问题提出、模型建构、解释验证;运算法则、运算策略;几何直观、空间想象;获取数据、加工数据、解释数据。

所有的数学核心素养都是建立在数学知识学习的基础上的，因此该评价模型的基础层为数与代数、图形与几何、统计与概率，即三大数学知识领域。

（2）构造数学核心素养评价指标判断矩阵

在数学核心素养评价指标的模型建构之后，进一步构造其判断矩阵，旨在判断各评价指标之间的相对重要性。因为数学核心素养评价的各一级指标权重相同，故设一级指标：数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析的权重分别为1/6。这个数值是以“1”为单位，确定6个数学核心素养一级指标权重，该数据只是相对数值，并不是Yaaph层次分析的权重，仅表明数学核心素养的6个一级指标同等重要。

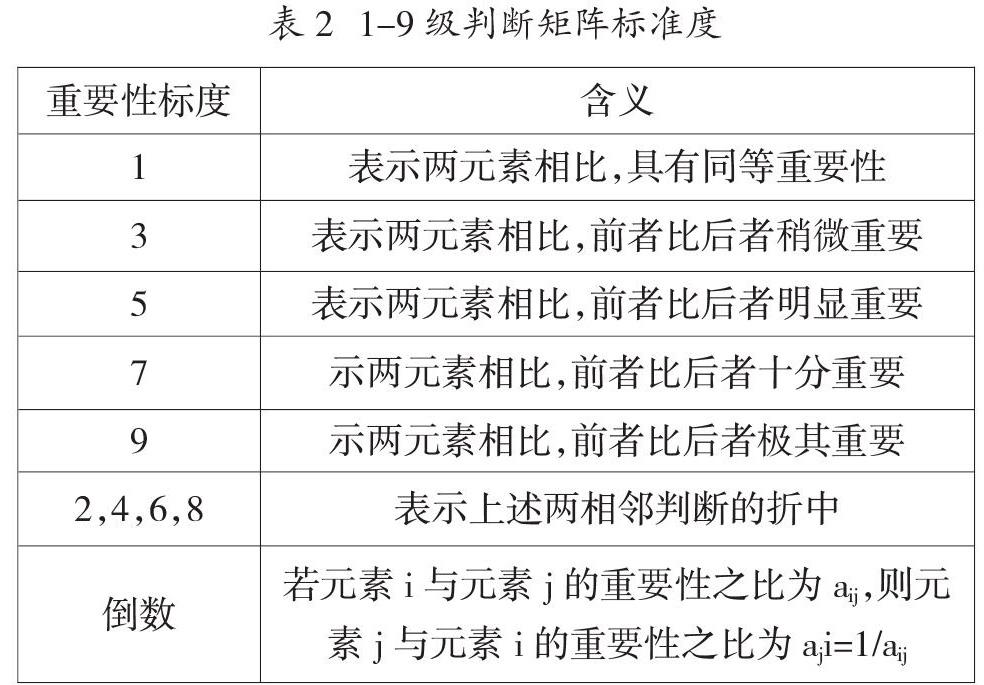
对数学核心素养评价二级指标的权重计算中，采用萨蒂提出的1-9标度法构建两两判断矩阵，各级标度的含义如表2所示。

通过确定初始权数来构造判断矩阵，采用专家打分与多因素统计相结合的方法，计算每个数学核心素养评价二级指标的重要度，从而得到初始权数，重要度的结果如表3所示。

得到初始权数之后，依据初始权数的大小按照结构指标分类参照1-9标度法对指标进行两两比较，从而建立判断矩阵。

由图2可知，初始权数最小值为3.537，最大值为4.037，则对区间[3.537，4.037]平均划分为10等分，在两两对比时，依据每个指标项的初始权数所在的区间来判断其标度。

以数学核心素养评价以及指标“数学抽象”下的各指标为例，数学表征和抽象思考的初始权数分别为4.037、3.9444，分别属于区间10、9内，计算其两两之间的绝对值差，若绝对值差为0或1，则认为两个元素具有同等的重要性。依据1-9标度法，得到“数学抽象”各指标的判断矩阵如表4所示。

从上表可知，数学表征与抽象思考相比，具有同等重要性。同理，对逻辑推理、数学建模、数学运算、直观想象、数据分析的各个指标，用1-9标度法进行两两比较，得到各指标的判断矩阵。

（3）计算数学核心素养评价指标的层次单排序

在构造数学核心素养评价指标的判断矩阵之后，进一步计算评价指标之间的层次单排序，旨在判断各个二级评价指标之间的关系，与评价指标数学抽象为例，进行分析，得到结果如表5所示。

由上表可知，数学表征和抽象思考对数学抽象的影响程度相同，权重均为0.5。矩阵通过一致性检验，即结果可信。同理，再对逻辑推理、数学建模、数学运算、直观想象、数据分析各指标进行权重及一致性分析。

（4）数学核心素养评价指标的层次总排序

在对数学核心素养评价指标进行层次单排序之后，再进行层次总排序，旨在判断各个二级评价指标相对于目标层的权重。对数学核心素养评价指标进行层次总排序，得到分析结果如表6所示。

综上，初步完成了数學核心素养评价指标体系的构建，其一级、二级评价指标的具体内容以及核心素养评价指标的权重如图3所示。

5.信度与效度分析

（1）信度分析

本研究利用SPSS 22.0对《数学核心素养评价二级指标咨询意见表》（6个一级指标，14个二级指标）进行信度分析，分析指标主要有内部一致性系数、分半信度。问卷样本总体的一致性系数0.993>0.8，说明问卷整体样本的信度较高。

《数学核心素养评价二级指标咨询意见表》的信度分析结果见表7，数学核心素养各评价指标内部一致性系数在0.946～0.978之间，总量表内部一致性系数为0.993。可见，数学核心素养评价量表的α信度指标基本达到了测量学要求。

（2）效度分析

在设计数学核心素养二级指标体系的时候，已经征求了专家的意见，他们对内容效度进行了评价，保证了该指标体系具有较高的内容效度。

四、结论与启示

1.数学核心素养二级指标的分类是评价模型建立的基础

在构建数学核心素养评价模型的过程中，二级指标的确定最为重要。《数学核心素养评价二级指标咨询意见表》正式版共计14个评价二级指标，各指标的内部一致性系数在0.946～0.978之间，说明数学核心素养各评价指标的整体概念一致并且具有很好的信度。结合专家评价，对评价指标的效度保障，《数学核心素养评价二级指标咨询意见表》达到测量学要求。在量表中，也对每一个数学核心素养评价指标下的二级指标进行了提炼、概括和闡释，对二级指标进行了层次排序，这也是数学核心素养评价体系和模型建构的基础。

根据每一个数学核心素养评价的一级指标的内涵及特征，划分其不同的二级指标;二级指标的划分首先基于一级指标特点的提炼，又能够反映一级指标的发展过程。数学核心素养评价指标具有整体性、变化性和递进性，每个一级指标相互之间形成整体，均指向数学核心素养的评价;每个二级指标之间也是变化着的，随着数学知识、数学能力的变化而发生深度和广度的变化。

2.数学核心素养评价指标的不同权重是评价模型建构的关键

通过建立一个评价模型，设定每个评价指标的权重，从而构建较为完整的数学核心素养评价体系。通过Yaahp层次分析，构造数学核心素养评价指标的判断矩阵，通过对评价指标的层次单排序、层次总排序，得到评价指标的综合权重。由此，可以进一步建立数学核心素养评价公式如下：

（C：数学核心素养;A：数学抽象;L：逻辑推理;M：数学建模;O：数学运算;I：直观想象;D：数据分析;V1：数学表征;V2：抽象思考。V3：合情推理;V4：演绎推理。V5：问题提出;V6：模型建构;V7：解释验证。V8：运算法则;V9：运算策略。V10：几何直观;V11：空间想象。V12：获取数据;V13：加工数据;V14：解释数据。）

总体而言，数学核心素养可以通过这14个二级指标来评价，上面的公式就是初步评价数学核心素养的基本依据。当然，考虑到数学核心素养的评价，与数学教学实际、教学任务难度、年级等因素相关，各个指标承担的功能也会有差异。数学核心素养的评价指标也是递进的，既有区别又有联系，在不同的权重之间，构建起数学核心素养评价模型的关系矩阵。所以，每一个指标的权重，还需要在大规模测试、调研后不断修正，使得这个评价模型更加科学、合理。

参考文献

[1] DeSeCo.The Definition and Selection of Key Competencies Executive Summary[EB/OL].（2003-06-25）.https：//www.pisa oecd org/data oecd/47/61/35070367.pdg.

[2] 中华人民共和国教育部.普通高中数学课程标准（2017年版）[S].北京：人民教育出版社，2018.

[3] 苏洪雨.学生几何素养的内涵与评价研究[D].上海：华东师范大学，2009.

[4] 桂德怀.中学生代数素养内涵与评价研究[D].上海：华东师范大学，2011.

[作者：陈蓓（1981-），女，江苏金坛人，江苏第二师范学院，教学质量监测与评估处，副研究员，博士。]

【责任编辑  刘永庆】